Дата: 07.02.2019
Класс: 10
Тема: Кодирование и обработка числовой информации. Представление информации с помощью систем счисления.
Цели:
познакомить с понятием система счисления;
познакомить с кодированием числовой информации;
познакомить с правилом перевода из одной системы счисления в другую;
формировать навыки работы на ПК;
Задачи:
Образовательные:
познакомить с системами счисления, используемыми в ПК для кодирования чисел;
изучить правила перевода из десятичной системы счисления в систему с любым основанием и наоборот.
Развивающие:
развивать логическое и теоретическое мышление;
уметь высказывать несогласие, сомнение, согласие с мнениями другого человека;
развивать навыки самостоятельной работы на ПК.
Воспитательные:
Оборудование: 9 компьютер, проектор, экран, интерактивная доска, презентация.
ХОД УРОКА
I. Организационный момент:
– Здравствуйте ребята, сегодня на уроке мы с вами вспомним, как числовая информация представляется в памяти компьютера, поговорим о системах счисления, изучим правила перевода из одной системы счисления в другую и по пройденной теме выполним практическую работу на ПК. Откройте свои тетради, запишите сегодняшнее число и тему урока: «Кодирование и обработка числовой информации. Представление информации с помощью систем счисления». Перед тем как мы с вами приступим к изучению новой темы, давайте повторим.
II. Актуализация знаний: по теме «Хранение информации»
1) Что такое информация? (Сведения об окружающем нас мире.)
2) Что такое данные? (Информация, хранящаяся в памяти компьютера)
3) Какие типы данных вам известны? (текстовая, числовая, графическая, видео, звуковая)
4) Как в памяти компьютера кодируется текстовая и графическая информация? (При помощи двоичного кода)
III. Объяснение нового материала:
Для записи информации о количестве объектов используются числа. Числа записываются с использованием особых знаковых систем, которые называются системами счисления. Алфавит системы счисления состоит из символов, которые называются цифрами.
Система счисления – это знаковая система, в которой числа записываются по определенным правилам с помощью символов некоторого алфавита, называемых цифрами.
Все системы счисления делятся на две большие группы: позиционные и непозиционные. В позиционных системах счисления количественное значение цифры зависит ото ее положения в числе, а в непозиционных- не зависит.
Непозиционные системы счисления. Примером непозиционной системы, которая сохранилась до наших дней, может служить римская система счисления, которая начала применяться более двух с половиной тысяч лет назад в Древнем Риме. В основе римской системы счисления лежат знаки I (один палец) для числа 1, V (раскрытая ладонь) для числа 5, X (две сложенные ладони) для числа 10, а для обозначения чисел 50,100,500 и 1000 используются латинские буквы L, C, D и M.
В римской системе счисления количественное значение цифры не зависит от ее положения в числе. Например, в римском числе ХХХ (30) цифра Х встречается трижды и в каждом случае обозначает одну и ту же величину- число 10, три раза по 10 в сумме 30.
Позиционные системы счисления. Каждая позиционная система счисления имеет определенный алфавит цифр (знаков) в ее алфавите.
В позиционных системах счисления количественное значение цифры зависит от ее позиции в числе. Позиция цифры в числе называется разрядом. Разряды числа возрастают справа налево, от младших разрядов к старшим. Основание показывает, во сколько раз изменяется значение цифры при перемещении ее в соседний разряд.
В настоящее время наиболее распространенными позиционными системами счисления является десятичная и двоичная. Десятичная система счисления имеет алфавит цифр, который состоит из арабских, цифр (0, 1, 2, 3, 4, 5, 6, 7, 8, 9), а двоичная – две цифры (0, 1).
Десятичная система счисления. В десятичной системе счисления цифра в крайней справа позиции обозначает единицы, цифра, смещенная на одну позицию влево, обозначает десятки, еще левее – сотни, затем – тысячи и т.д.
В развёрнутой форме записи числа умножение цифр числа на основание производится в явной форме.
Развёрнутая форма числа в системе счисления с основанием q (q-ичная система счисления) записывается следующим образом:
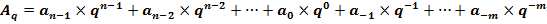
где Aq – число в q-ичной системе счисления;
q – основание системы счисления;
n – число целых разрядов числа;
m – число дробных разрядов числа.
Свёрнутая форма записи числа
Свёрнутая форма записи числа называется запись в виде: 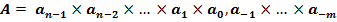
Основание: q = 10
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Число в десятичной системе счисления записывается в виде суммы числового ряда степеней (в данном случае 10), в качестве коэффициентов которых выступают цифры данного числа.
Развёрнутая форма записи числа A10
В развёрнутой форме запись числа A10, которое содержит n целых разрядов числа и m дробных разрядов числа, имеет следующий вид:
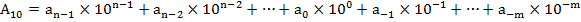
Пример:
333,3310 = 3*102 + 3*101 + 3*100 + 3*10-1 + 3*10-2
Двоичная система счисления
Основание: q = 2
Алфавит: 0, 1
Число в двоичной системе счисления записывается в виде суммы числового ряда степеней (в данном случае 2), в качестве коэффициентов которых выступают цифры данного числа.
Развёрнутая форма записи числа A2
В развёрнутой форме запись числа A2, которое содержит n целых разрядов числа и m дробных разрядов числа, имеет следующий вид:
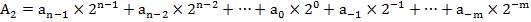
Пример:
100010012 = 1*27 + 0*26 + 0*25 + 0*24 + 1*23 + 0*22 + 0*21 + 1*20
10011012 = 1*26 + 0*25 + 0*24 + 1*23 + 1*22 + 0*21 + 1*20
Перевод целых чисел из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную.
Перевод чисел из десятичной системы в двоичную, восьмеричную и шестнадцатеричную может осуществляться различными способами.
Алгоритм перевода целых десятичных чисел в двоичную, восьмеричную и шестнадцатеричную системы счисления следующий:
1. Последовательно выполнять деление исходного целого десятичного числа и получаемых целых частных на основании системы (на 2, 8, 16) до тех пор, пока не получим частное, равное нулю.
2. Получить искомое двоичное, восьмеричное или шестнадцатеричное число, для чего записать полученные остатки обратной последовательность.
Пример1:
Переведем число 15910 в с.с. с основанием 2:

Запишем остатки, начиная с последнего – 10011111, то есть 15910 = 100111112
Пример2:
Переведем число 61510 в с.с. с основанием 8:

Получаем, число 61510=11478
Пример3:
Переведем число 1967310 в с.с. с основанием 16:

Получаем, число 1967310=4СВ916
Для перевода из двоичной системы счисления в восьмеричную необходимо разбить число на группы по три цифры (триады), справа на лево, если в последней левой группе окажется меньше чем три разряда, то необходимо её дополнить слева нулями.
| Десятичная система счисления | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Двоичные триады | 000 | 001 | 010 | 011 | 100 | 101 | 110 | 111 |
Пример:
1010012 = 518
1101012 = 658
1001011,0112 = 113,38
Перевод чисел из двоичной системы счисления в шестнадцатеричную
Для перевода целого двоичного числа в шестнадцатеричное его нужно разбить на группы по четыре цифры (тетрады), начиная справа; если в последней левой группе окажется меньше разрядов, надо дополнить её слева нулями.
| Шестнадцатеричные цифры | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
| Двоичные тетрады | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
Пример:
1010012 = 2916
1111010101,112 = 3D5,C16
IV. Закрепление изученного материала
Самостоятельная работа
В1
Как представлено число 8310 в двоичной системе счисления?
10010112 2) 11001012 3) 10100112 4) 1010012
Сколько единиц в двоичной записи числа 195?
5 2) 2 3) 3 4) 4
Вычислите сумму чисел x и y, при x = A616, y = 758. Результат представьте в двоичной системе счисления.
110110112 2) 111100012 3) 111000112 4) 100100112
Дано: а = 2110, b = 238. Какое из чисел, записанных в двоичной системе, отвечает условию b c a?
10000 2) 10001 3) 11000 4) 10100
В-2
Как представлено число 2510 в двоичной системе счисления?
1) 10012 2) 110012 3) 100112 4) 110102
Количество значащих нулей в двоичной записи десятичного числа 126 равно
1) 1 2) 2 3) 3 4) 0
Вычислите сумму чисел x и y, при x = 1D16, y = 728. Результат представьте в двоичной системе счисления.
100011112 2) 11001012 3) 1010112 4) 10101112
Дано: а = 1510, b = 118. Какое из чисел, записанных в двоичной системе, отвечает условию b c a?
1111 2) 1100 3) 1001 4) 1000
В-3
Как представлено число 6710 в двоичной системе счисления?
10000112 2) 11001012 3) 10100112 4) 10100012
Сколько единиц в двоичной записи числа 189?
5 2) 6 3) 3 4) 4
Вычислите сумму чисел x и y, при x = В516, y = 748. Результат представьте в двоичной системе счисления.
110110112 2) 111100012 3) 111000112 4) 100100112
Дано: а = 1510, b = 128. Какое из чисел, записанных в двоичной системе, отвечает условию b c a?
1111 2) 1001 3) 1000 4) 1100
В - 4
Как представлено число 5110 в двоичной системе счисления?
1) 1100012 2) 1100112 3) 1001112 4) 1100102
Количество значащих нулей в двоичной записи десятичного числа 152 равно
1) 1 2) 2 3) 3 4) 5
Вычислите сумму чисел x и y, при x = 2Е16, y = 738. Результат представьте в двоичной системе счисления.
110011112 2) 11010012 3) 11010112 4) 10110012
Дано: а = 6910, b = 408. Какое из чисел, записанных в двоичной системе, отвечает условию b ca?
1 000 000 2) 1 000 110 3) 1 000 101 4) 1 000 111
Ключ:
1 вариант. 1.3) 2.4) 3. 166+61=227 3) 4.4)
2 вариант. 1.2) 2.1) 3. 29+58=87 4) 4. 2)
3 вариант. 1.1) 2. 2) 3. 181+60=241 2) 4. 4)
4 вариант. 1. 2) 2. 4) 3. 46+59=105 2) 4. 1)
V. Подведение итогов
Вопросы:
1. Дать определение систем счисления. Назвать и охарактеризовать свойства системы счисления?
2. Какие символы используются для записи чисел в двоичной системе счисления? Восьмеричной? Шестнадцатеричной?
Выставление оценок и организация ДЗ:
Преобразуйте следующие десятичные числа в двоичные (восьмеричные, шестнадцатеричные): 0, 1, 18, 25, 128?



















