Mekdebi№:_______ Senesi: ______ _______ _______
Dersiň ady: Geometriýa Synpy:9-njy synp ______ _______ _______
| Sapagyň temasy: | Proporsional kesimler. Meňzeş üçburçluklar |
| Sapagyň maksatlary: |
|
| 1)Bilim berijilik maksady: | Proporsional kesimler. Meňzeş üçburçluklar hakynda düşünjeleri öwretmek. Okuwçylaryň öňki öwrenenlerini berkitmek, olaryň başarnyklaryny, ukyplaryny ösdürmek. |
| 2) Terbiýeçilik maksady: | Okuwçylary watançylyk, zähmetsöýerlik, beýik adamkärçilik ruhunda terbiýelemek. Olaryň watansöýüjilik duýgularyny ösdürmek. |
| Sapagyň görnüşi: | Täze maglumatlary öwretmek sapagy |
| Sapakda ulanylýan okuw-görkezme esbaplar, sanly serişdeler, paýlama maglumatlar: | Kompýuter, interaktiw tagta, slaýdlar, tanyşdyrmalar, tablisalar, tema degişli soraglar, çyzgyç. |
Sapagyň gidişi:
1. Sapagyň guramaçylyk döwri:
1. Salamlaşmak. Gatnaşygy hasaba almak. 2. Okuwçylaryň sapaga taýýarlygyny barlamak.
3. Okuwçylaryň ünsüni sapaga gönükdirmek. 4. Syýasy wakalar bilen tanyşdyrmak.
2. Öý işiniň ýerine ýetirilişini barlamak:
Geçilenleri gaýtalamak
3. Geçilen temany jemlemek:
Geçilenleri gaýtalamak
4. Täze temany düşündirmek:
Temany düşündirmegiň meýilnamasy:
1. Proporsional kesimleri öwretmek
2. Meňzeş üçburçluklary öwretmek
3. Meňzeş üçburçluklaryň kesgitlenilişini öwretmek
Temany öwrenmek bilen okuwçylar bilmeli:
- Nähili kesimlere proporsional kesimler diýilýändigini bilmeli
- Nähili figuralara meňzeş figuralar diýilýändigini bilmeli
- Nähili üçburçluklara meňzeş üçburçluklar diýilýändigini bilmeli
Temany öwrenmek bilen okuwçylar başarmaly:
- Üçburçluklaryň meňzeşligini kesgitlemegi başarmaly
- Proporsional kesimler bilen baglanyşykly meseleleri çözmegi başarmaly.
- Meňzeş üçburçluklar bilen baglanyşykly meseleleri çözmegi başarmaly.
1. Meňzeş üçburçluklaryň kesgitlenilişi. AB we CD
kesimleriň gatnaşygy diýlip olaryň uzynlyklarynyň gatnaşygyna,
ýagny 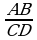 aýdylýar. Eger
aýdylýar. Eger 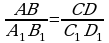 bolsa, onda AB we CD kesimler A1B1 we C1D1 kesimlere proporsional kesimler diýilýär. Mysal üçin, uzynlyklary 2 sm we 1 sm bolan AB we CD kesimler uzynlyklary 3 sm we 1,5 sm bolan А1В1 we С1D1 kesimlere proporsionaldyr. Sebäbi
bolsa, onda AB we CD kesimler A1B1 we C1D1 kesimlere proporsional kesimler diýilýär. Mysal üçin, uzynlyklary 2 sm we 1 sm bolan AB we CD kesimler uzynlyklary 3 sm we 1,5 sm bolan А1В1 we С1D1 kesimlere proporsionaldyr. Sebäbi 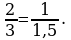
Proporsionallyk düşünjesi has köp kesimler üçin hem dogrudyr. Eger 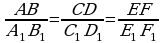 şert ýerine ýetse, onda AB, CD we EF üç kesim, degişlilikde A1B1, C1D1 we E1F1 üç kesime proporsionaldyr.
şert ýerine ýetse, onda AB, CD we EF üç kesim, degişlilikde A1B1, C1D1 we E1F1 üç kesime proporsionaldyr.
Bize gündelik durmuşda birmeňzeş görnüşli, ýöne dürli ölçeg li zatlar kän duş gelýär. Mysal üçin, futbol pökgüsi we ýerde oýnalýan tennisiň pökgüsi ölçeglerine seretmezden şol bir görnüşe eýedirler. Geometriýada şol bir görnüşli figuralara meňzeş figuralar diýlip at berilýär. Mysal üçin, islendik iki kwadrat ýa-da islendik iki tegelek meňzeşdirler.
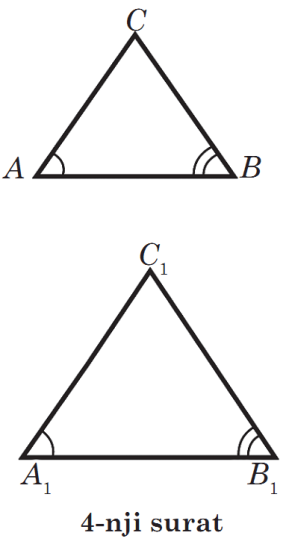
Goý, ABC we A1B1C1 iki üçburçlugyň degişli burçlary deň, ýagny ∠A =∠A1, ∠B =∠B1, ∠C =∠C1 bolsun. Şonda AB we A1B1, BC we B1C1, CA we C1A1 taraplara meňzeş taraplar diýilýär (1-nji surat).
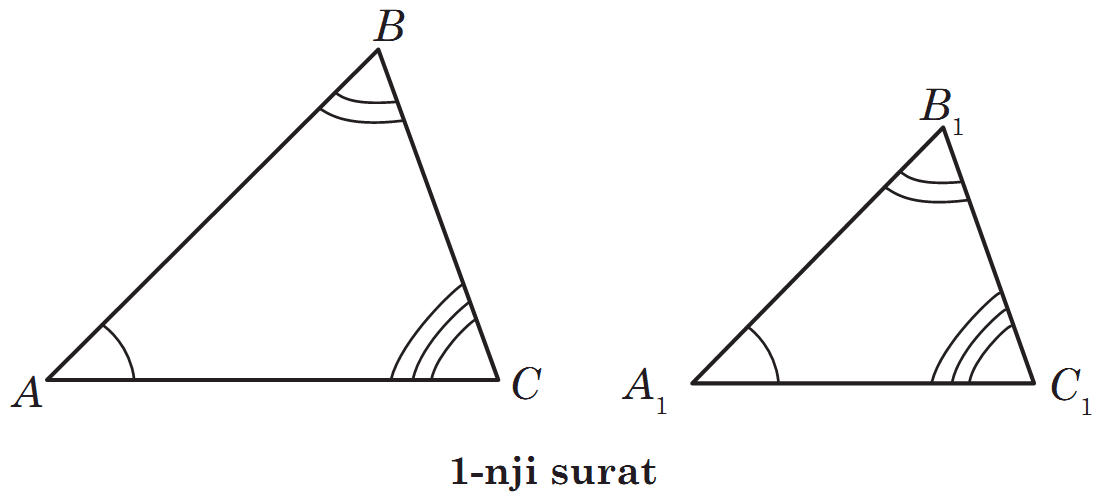
Kesgitleme: Eger iki üçburçlugyň degişli burçlary deň we meňzeş taraplary proporsional bolsa, onda olara meňzeş üçburç luklar diýilýär.
Başga sözler bilen aýdanymyzda, eger ∠A = ∠A1, ∠B =∠B1, ∠C =∠C1, we 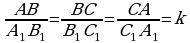 bolsa, onda ABC we A1B1C1 üçburçluklara meňzeş üçburçluklar diýilýär.
bolsa, onda ABC we A1B1C1 üçburçluklara meňzeş üçburçluklar diýilýär.
Üçburçluklaryň meňzeş taraplarynyň gatnaşygyna deň bolan k sana meňzeşlik koeffisiýenti diýilýär.
ABC we A1B1C1 üçburçluklaryň meňzeşligi ΔABC ~ ΔA1B1C1 görnüşde belgilenýär. 1-nji suratda meňzeş üçburçluklar şekillendirilendir.
5. Täze temany berkitmek:
1. 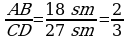
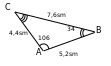 Eger bu kesimleriň uzynlyklary santimetrlerde dälde millimetrlerde aňladylsa, bu gatnaşyk üýtgemez.
Eger bu kesimleriň uzynlyklary santimetrlerde dälde millimetrlerde aňladylsa, bu gatnaşyk üýtgemez.
4.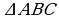 -yň
-yň 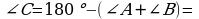
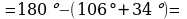
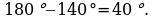
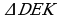 -yň
-yň
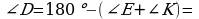
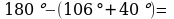
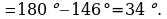
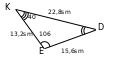
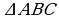 we
we 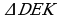 -yň degişli burçlary deň.
-yň degişli burçlary deň.
Degişli taraplarynyň proporsionallygyny barlalyň.
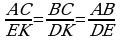 ýa-da
ýa-da 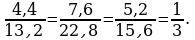
Diýmek bu üçburçluklaryň degişli taraplary hem proporsional
onda olar meňzeşdirler. ABC ~ DEK
6. Öý işini tabşyrmak:
1. Nähili kesimlere proporsional kesimler diýilýär?
2. Nähili figuralara meňzeş figuralar diýilýär?
3. Nähili üçburçluklara meňzeş üçburçluklar diýilýär?
Üçburçluklaryň meňzeşligi nähili belgilenýär?
7. Sapagy jemlemek, umumylaşdyrmak, okuwçylary bahalandyrmak:
Soraglara takyk, dogry jogap beren, sapakda işjeňlik görkezip, temany gürrüň bermäge işjeň gatnaşan okuwçylar atlandyrylyp, olar bahalandyrylýar (bahalar synp žurnalyna, gündeliklere goýulýar).
Ýazan mugallym: ___________________________________________________
Bellik:________________________________________________________________
Barlan: Müdiriň okuw işleri baradaky orunbasary ____________________________
Mekdebi№:_______ Senesi: ______ _______ _______
Dersiň ady: Geometriýa Synpy:9-njy synp ______ _______ _______
| Sapagyň temasy: | Meňzeş üçburçluklaryň meýdanlarynyň gatnaşygy |
| Sapagyň maksatlary: |
|
| 1)Bilim berijilik maksady: | Meňzeş üçburçluklaryň meýdanlarynyň gatnaşygy hakynda düşünjeleri öwretmek. Okuwçylaryň öňki öwrenenlerini berkitmek, olaryň başarnyklaryny, ukyplaryny ösdürmek. |
| 2) Terbiýeçilik maksady: | Okuwçylary watançylyk, zähmetsöýerlik, beýik adamkärçilik ruhunda terbiýelemek. Olaryň watansöýüjilik duýgularyny ösdürmek. |
| Sapagyň görnüşi: | Täze maglumatlary öwretmek sapagy |
| Sapakda ulanylýan okuw-görkezme esbaplar, sanly serişdeler, paýlama maglumatlar: | Kompýuter, interaktiw tagta, slaýdlar, tanyşdyrmalar, tablisalar, tema degişli soraglar, çyzgyç. |
Sapagyň gidişi:
1. Sapagyň guramaçylyk döwri:
1. Salamlaşmak. Gatnaşygy hasaba almak. 2. Okuwçylaryň sapaga taýýarlygyny barlamak.
3. Okuwçylaryň ünsüni sapaga gönükdirmek. 4. Syýasy wakalar bilen tanyşdyrmak.
2. Öý işiniň ýerine ýetirilişini barlamak:
1. Nähili kesimlere proporsional kesimler diýilýär?
2. Nähili figuralara meňzeş figuralar diýilýär?
3. Nähili üçburçluklara meňzeş üçburçluklar diýilýär?
Üçburçluklaryň meňzeşligi nähili belgilenýär?
3. Geçilen temany jemlemek:
Proporsional kesimler. Meňzeş üçburçluklar
4. Täze temany düşündirmek:
Temany düşündirmegiň meýilnamasy:
1. Meňzeş üçburçluklaryň meýdanlarynyň gatnaşygyny öwretmek
2. Meňzeş üçburçluklary öwretmek
3. Meňzeş üçburçluklaryň meýdanlarynyň gatnaşygyny tapmagy öwretmek
Temany öwrenmek bilen okuwçylar bilmeli:
- Meňzeş üçburçluklaryň meýdanlarynyň gatnaşygyny bilmeli
- Meňzeş iki üçburçlugyň meýdanlarynyň gatnaşygy olaryň meňzeşlik koeffisiýentiniň kwadratyna deňdigini bilmeli
- Nähili üçburçluklara meňzeş üçburçluklar diýilýändigini bilmeli
Temany öwrenmek bilen okuwçylar başarmaly:
- Meňzeş üçburçluklaryň meýdanlarynyň gatnaşygyny tapmagy başarmaly
- Meňzeş üçburçluklaryň meýdanlarynyň gatnaşygy bilen baglanyşykly meseleleri çözmegi başarmaly.
- Meňzeş üçburçluklar bilen baglanyşykly meseleleri çözmegi başarmaly.
1-nji teorema. Meňzeş iki üçburçlugyň meýdanlarynyň gatnaşygy olaryň meňzeşlik koeffisiýentiniň kwadratyna deňdir.
Goý, ABC we A1B1C1 üçburçluklar meňzeş bolup, olaryň meňzeşlik koeffisiýenti k sana deň bolsun. Bu üçburçluklaryň meýdanlaryny S we S1 bilen belgiläliň. Deň burçlary bolan üçburçluklaryň meýdanlarynyň gatnaşygy baradaky teore
ma görä, A=A1 bolany üçin,
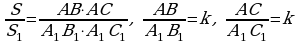 bolany üçin,
bolany üçin, 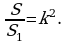 Teorema subut edildi.
Teorema subut edildi.
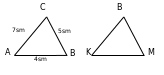 5. Täze temany berkitmek:
5. Täze temany berkitmek:
5. 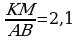 ,
,
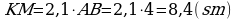
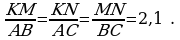
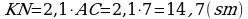
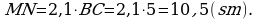
Jogaby: 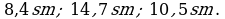
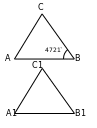
 6. Subudy. ABC~KMN bolsun, onda
6. Subudy. ABC~KMN bolsun, onda
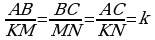
bolar.
Meňzeş üçburçluklaryň meýdanlarynyň gatnaşyklary
olaryň meňzeşlik koeffisiýentleriniň kwadratlaryna deňdir.
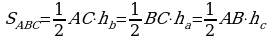
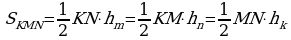
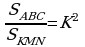 ýa–da
ýa–da 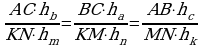
Bu gatnaşyk K2 deňdir, ýagny
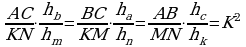 (*)
(*)
 emma
emma 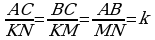 bolany üçin (*) deňligi K bölüp alarys:
bolany üçin (*) deňligi K bölüp alarys: 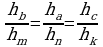 Subut etmeli hem şudy.
Subut etmeli hem şudy.
7. (Shu meselanin shertinde kabir
maglumat düzedilmeli)
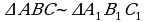 bolany üçin
bolany üçin
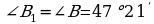 deň bolar.
deň bolar.
Üçburçluklaryň meňzeşlik
koeffisiýenti 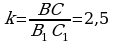
deňdir. Onda 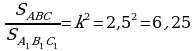
(9-njy meselaniň şertine meňzeş şert 7-njide hem bolmaly)
6. Öý işini tabşyrmak:
1. Nähili kesimlere proporsional kesimler diýilýär?
2. Nähili figuralara meňzeş figuralar diýilýär?
3. Nähili üçburçluklara meňzeş üçburçluklar diýilýär?
Üçburçluklaryň meňzeşligi nähili belgilenýär?
7. Sapagy jemlemek, umumylaşdyrmak, okuwçylary bahalandyrmak:
Soraglara takyk, dogry jogap beren, sapakda işjeňlik görkezip, temany gürrüň bermäge işjeň gatnaşan okuwçylar atlandyrylyp, olar bahalandyrylýar (bahalar synp žurnalyna, gündeliklere goýulýar).
Ýazan mugallym: ___________________________________________________
Bellik:________________________________________________________________
Barlan: Müdiriň okuw işleri baradaky orunbasary ____________________________
Mekdebi№:_______ Senesi: ______ _______ _______
Dersiň ady: Geometriýa Synpy:9-njy synp ______ _______ _______
| Sapagyň temasy: | Üçburçlugyň bissektrisasynyň häsiýeti |
| Sapagyň maksatlary: |
|
| 1)Bilim berijilik maksady: | Üçburçlugyň bissektrisasynyň häsiýeti hakynda düşünjeleri öwretmek. Okuwçylaryň öňki öwrenenlerini berkitmek, olaryň başarnyklaryny, ukyplaryny ösdürmek. |
| 2) Terbiýeçilik maksady: | Okuwçylary watançylyk, zähmetsöýerlik, beýik adamkärçilik ruhunda terbiýelemek. Olaryň watansöýüjilik duýgularyny ösdürmek. |
| Sapagyň görnüşi: | Täze maglumatlary öwretmek sapagy |
| Sapakda ulanylýan okuw-görkezme esbaplar, sanly serişdeler, paýlama maglumatlar: | Kompýuter, interaktiw tagta, slaýdlar, tanyşdyrmalar, tablisalar, tema degişli soraglar, çyzgyç. |
Sapagyň gidişi:
1. Sapagyň guramaçylyk döwri:
1. Salamlaşmak. Gatnaşygy hasaba almak. 2. Okuwçylaryň sapaga taýýarlygyny barlamak.
3. Okuwçylaryň ünsüni sapaga gönükdirmek. 4. Syýasy wakalar bilen tanyşdyrmak.
2. Öý işiniň ýerine ýetirilişini barlamak:
1. Nähili kesimlere proporsional kesimler diýilýär?
2. Nähili figuralara meňzeş figuralar diýilýär?
3. Nähili üçburçluklara meňzeş üçburçluklar diýilýär?
Üçburçluklaryň meňzeşligi nähili belgilenýär?
3. Geçilen temany jemlemek:
Meňzeş üçburçluklaryň meýdanlarynyň gatnaşygy
4. Täze temany düşündirmek:
Temany düşündirmegiň meýilnamasy:
1. Üçburçlugyň bissektrisasynyň häsiýetini öwretmek
2. Meňzeş üçburçluklary öwretmek
3. Üçburçlugyň bissektrisasy garşysyndaky tarapy sepleşýän taraplara proporsional bolan kesimlere bölýändigini subut etmegi öwretmek
Temany öwrenmek bilen okuwçylar bilmeli:
- Üçburçlugyň bissektrisasynyň häsiýetini bilmeli
- Üçburçlugyň bissektrisasy garşysyndaky tarapy sep leşýän taraplara proporsional bolan kesimlere bölýändigini bilmeli
- Nähili üçburçluklara meňzeş üçburçluklar diýilýändigini bilmeli
Temany öwrenmek bilen okuwçylar başarmaly:
- Üçburçlugyň bissektrisasy garşysyndaky tarapy sepleşýän taraplara proporsional bolan kesimlere bölýändigini subut etmegi başarmaly
- Meňzeş üçburçluklaryň meýdanlarynyň gatnaşygy bilen baglanyşykly meseleleri çözmegi başarmaly.
- Meňzeş üçburçluklar bilen baglanyşykly meseleleri çözmegi başarmaly.
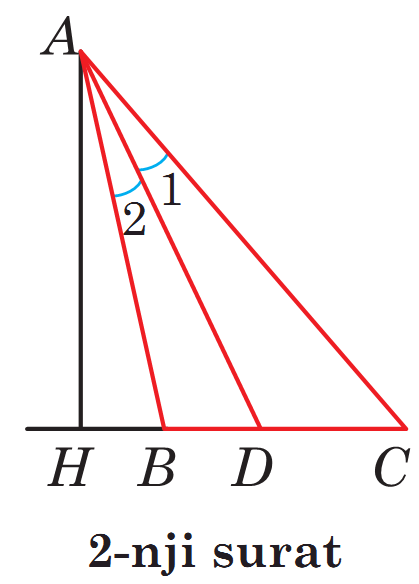 2-nji teorema. Üçburçlugyň bissektrisasy garşysyndaky tarapy sep leşýän taraplara proporsional bolan kesimlere bölýär.
2-nji teorema. Üçburçlugyň bissektrisasy garşysyndaky tarapy sep leşýän taraplara proporsional bolan kesimlere bölýär.
Goý, AD kesim ABC üçburçlugyň bissektrisasy bolsun (2-nji surat). 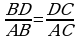 bolýandygyny subut edeliň. ABD we ACD üçburçluklaryň umumy AH beýikligi bolany üçin:
bolýandygyny subut edeliň. ABD we ACD üçburçluklaryň umumy AH beýikligi bolany üçin:
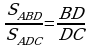 (1)
(1)
Başga tarapdan ∠1 = ∠2 bolany üçin:
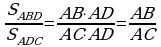 (2)
(2)
(1) we (2) deňliklerden 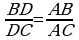 ýa-da
ýa-da 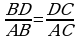
deňligi alarys. Teorema subut edildi.
5. Täze temany berkitmek:
3. a) Üçburçlugyň bissektrisasynyň häsiýeti boýunça:
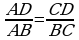 ,
, 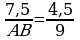 .
.
AB=7,5•2= 15sm. Jogaby:15sm.
b)BDC=C bolany üçin BDC deňýanly:
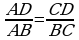 formuladan
formuladan 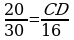 alarys. CD=16•
alarys. CD=16•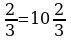 sm. Jogaby:
sm. Jogaby: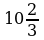 sm.
sm.
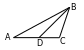 8. AC=AD+DC=7,5+2,5=10sm.
8. AC=AD+DC=7,5+2,5=10sm.
AB+BC=P-AC=25-10=15sm.
AD:AB=CD:BC, 7,5:AB=2,5:BC.
AB=3BC; AB+BC=4BC=15sm;
BC=3,75sm. AB=15-3,75=11,25sm.
Jogaby: 11,25sm; 3,75sm; 10sm.
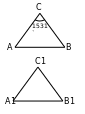 9.
9. 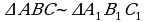 bolany üçin
bolany üçin 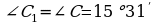 deň bolar.
deň bolar.
Üçburçluklaryň meňzeşlik koeffisiýenti
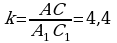 deňdir. Onda
deňdir. Onda 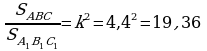 ,
,
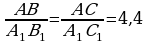 ýa–da
ýa–da 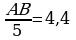 , AB=22sm.
, AB=22sm.
Jogaby: 1531′; 22sm; 19,36.
10. AC=P-(AB+BC)=35-(12+16)=7sm. AD=x,
CD=7-x. x:12=(7-x):16; x=3sm. AD=3sm. CD=4sm.
Jogaby: 3sm, 4sm.
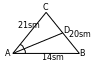 11. Üçburçlugyň bissektrisasynyň
11. Üçburçlugyň bissektrisasynyň
häsiýeti baradaky teorema görä ýazýarys:
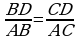 ýa–da
ýa–da 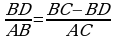
Soňky deňlikde san bahalary ýerine
goýup alarys:
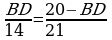 ,
, 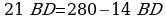 ,
, 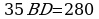 ,
, 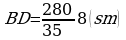 .
. 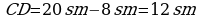 . Jogaby: 8sm; 12sm.
. Jogaby: 8sm; 12sm.
6. Öý işini tabşyrmak:
1. Nähili kesimlere proporsional kesimler diýilýär?
2. Nähili figuralara meňzeş figuralar diýilýär?
3. Nähili üçburçluklara meňzeş üçburçluklar diýilýär?
4. Üçburçluklaryň meňzeşligi nähili belgilenýär?
5. Meňzeş üçburçluklaryň meýdanlary nähili gatnaşýarlar?
7. Sapagy jemlemek, umumylaşdyrmak, okuwçylary bahalandyrmak:
Soraglara takyk, dogry jogap beren, sapakda işjeňlik görkezip, temany gürrüň bermäge işjeň gatnaşan okuwçylar atlandyrylyp, olar bahalandyrylýar (bahalar synp žurnalyna, gündeliklere goýulýar).
Ýazan mugallym: ___________________________________________________
Bellik:________________________________________________________________
Barlan: Müdiriň okuw işleri baradaky orunbasary ____________________________
Mekdebi№:_______ Senesi: ______ _______ _______
Dersiň ady: Geometriýa Synpy:9-njy synp ______ _______ _______
| Sapagyň temasy: | Üçburçluklaryň meňzeşlik nyşanlary |
| Sapagyň maksatlary: |
|
| 1)Bilim berijilik maksady: | Üçburçluklaryň meňzeşlik nyşanlary hakynda düşünjeleri öwretmek. Okuwçylaryň öňki öwrenenlerini berkitmek, olaryň başarnyklaryny, ukyplaryny ösdürmek. |
| 2) Terbiýeçilik maksady: | Okuwçylary watançylyk, zähmetsöýerlik, beýik adamkärçilik ruhunda terbiýelemek. Olaryň watansöýüjilik duýgularyny ösdürmek. |
| Sapagyň görnüşi: | Täze maglumatlary öwretmek sapagy |
| Sapakda ulanylýan okuw-görkezme esbaplar, sanly serişdeler, paýlama maglumatlar: | Kompýuter, interaktiw tagta, slaýdlar, tanyşdyrmalar, tablisalar, tema degişli soraglar, çyzgyç. |
Sapagyň gidişi:
1. Sapagyň guramaçylyk döwri:
1. Salamlaşmak. Gatnaşygy hasaba almak. 2. Okuwçylaryň sapaga taýýarlygyny barlamak.
3. Okuwçylaryň ünsüni sapaga gönükdirmek. 4. Syýasy wakalar bilen tanyşdyrmak.
2. Öý işiniň ýerine ýetirilişini barlamak:
1. Nähili kesimlere proporsional kesimler diýilýär?
2. Nähili figuralara meňzeş figuralar diýilýär?
3. Nähili üçburçluklara meňzeş üçburçluklar diýilýär?
4. Üçburçluklaryň meňzeşligi nähili belgilenýär?
5. Meňzeş üçburçluklaryň meýdanlary nähili gatnaşýarlar?
 3. Geçilen temany jemlemek:
3. Geçilen temany jemlemek:
Üçburçlugyň bissektrisasynyň häsiýeti
4. Täze temany düşündirmek:
Temany düşündirmegiň meýilnamasy:
1. Üçburçluklaryň meňzeşlik nyşanlaryny öwretmek
2. Üçburçluklaryň meňzeşlik nyşanlaryndan gelip çykýan netijeleri öwretmek
3. Üçburçluklaryň meňzeşliginiň birinji nyşanyny subut etmegi öwretmek
Temany öwrenmek bilen okuwçylar bilmeli:
- Üçburçluklaryň meňzeşlik nyşanlaryny bilmeli
- Üçburçluklaryň meňzeşlik nyşanlaryndan gelip çykýan netijeleri bilmeli
- Nähili üçburçluklara meňzeş üçburçluklar diýilýändigini bilmeli
Temany öwrenmek bilen okuwçylar başarmaly:
- Üçburçluklaryň meňzeşliginiň birinji nyşanyny subut etmegi başarmaly
- Üçburçluklaryň meňzeşliginiň ikinji nyşanyny subut etmegi başarmaly
- Üçburçluklaryň meňzeşliginiň üçünji nyşanyny subut etmegi başarmaly
Üçburçluklaryň meňzeşliginiň birinji nyşany
Teorema.Eger bir üçburçlugyň iki burçy degişlilikde beýleki üçburçlugyň iki burçuna deň bolsa, onda bu üçburçluklar meňzeşdirler.
1-nji netije. Deňtaraply üçburçluklar meňzeşdirler.
2-nji netije. Eger deňýanly üçburçluklaryň depesindäki ýa-da esasyndaky burçlary özara deň bolsa, onda ol üçburçluklar meňzeşdirler.
3-nji netije. Eger gönüburçly üçburçlugyň bir ýiti burçy beýleki bir gönüburçly üçburçlugyň bir ýiti burçuna deň bolsa, onda ol üçburçluklar meňzeşdirler.
Üçburçluklaryň meňzeşliginiň ikinji nyşany
Teorema. Eger bir üçburçlugyň iki tarapy beýleki üçburçlugyň iki tarapyna proporsional we bu taraplaryň arasyndaky burçlary deň bolsa, onda bu üçburçluklar meňzeşdirler.
Netije. Eger gönüburçly iki üçburçlugyň biriniň katetleri beýlekisiniň katetlerine proporsional bolsa, onda ol üçburçluklar meňzeşdirler.
Üçburçluklaryň meňzeşliginiň üçünji nyşany
Teorema. Eger bir üçburçlugyň üç tarapy beýleki üçburçlugyň üç tarapyna proporsional bolsa, onda bu üçburçluklar meňzeşdirler.
5. Täze temany berkitmek:
22. B=180-A-C=180-50-60=70, C=K=60, B=E=70
bolany üçin 1-nyşana görä ABC~DEK. S.E.Ş.
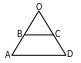 23.
23. 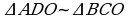 bolany üçin alarys:
bolany üçin alarys:
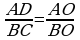 ,
, 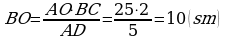
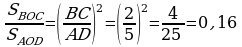
Jogaby: 10sm; 0,16
24. AOC=DOB (wertikal burçlar).
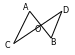
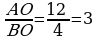 ;
; 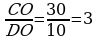
bolany üçin 2-nji nyşana görä AOC~BOD.
Meňzeş üçburçluklaryň degişli burçlary
deňdir: CAO=DBO=61.
Meňzeşlik koefisienti 3-e deň bolany üçin
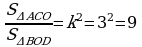 .
.
Jogaby: 61; 9.
25. 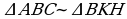 , sebäbi
, sebäbi 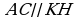 .
.
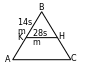 Onda
Onda 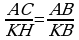 ,
,
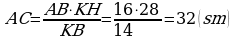
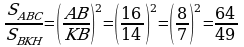 .
.
Jogaby: 32sm; 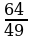 .
.
6. Öý işini tabşyrmak:
1. Üçburçluklaryň meňzeşliginiň birinji nyşanyny subut ediň.
2. Deňýanly üçburçluklaryň meňzeş bolmagy üçin haýsy şert ýerine ýetmeli?
3. Üçburçluklaryň meňzeşliginiň ikinji nyşanyny subut ediň.
4. Üçburçluklaryň meňzeşliginiň üçünji nyşanyny subut ediň.
5. Gönüburçly üçburçluklaryň meňzeş bolmagy üçin haýsy şert ýerine ýetmeli?
7. Sapagy jemlemek, umumylaşdyrmak, okuwçylary bahalandyrmak:
Soraglara takyk, dogry jogap beren, sapakda işjeňlik görkezip, temany gürrüň bermäge işjeň gatnaşan okuwçylar atlandyrylyp, olar bahalandyrylýar (bahalar synp žurnalyna, gündeliklere goýulýar).
Ýazan mugallym: ___________________________________________________
Bellik:________________________________________________________________
Barlan: Müdiriň okuw işleri baradaky orunbasary ____________________________
Mekdebi№:_______ Senesi: ______ _______ _______
Dersiň ady: Geometriýa Synpy:9-njy synp ______ _______ _______
| Sapagyň temasy: | Üçburçluklaryň meňzeşlik nyşanlary |
| Sapagyň maksatlary: |
|
| 1)Bilim berijilik maksady: | Üçburçluklaryň meňzeşlik nyşanlary hakynda düşünjeleri öwretmek. Okuwçylaryň öňki öwrenenlerini berkitmek, olaryň başarnyklaryny, ukyplaryny ösdürmek. |
| 2) Terbiýeçilik maksady: | Okuwçylary watançylyk, zähmetsöýerlik, beýik adamkärçilik ruhunda terbiýelemek. Olaryň watansöýüjilik duýgularyny ösdürmek. |
| Sapagyň görnüşi: | Täze maglumatlary öwretmek sapagy |
| Sapakda ulanylýan okuw-görkezme esbaplar, sanly serişdeler, paýlama maglumatlar: | Kompýuter, interaktiw tagta, slaýdlar, tanyşdyrmalar, tablisalar, tema degişli soraglar, çyzgyç. |
Sapagyň gidişi:
1. Sapagyň guramaçylyk döwri:
1. Salamlaşmak. Gatnaşygy hasaba almak. 2. Okuwçylaryň sapaga taýýarlygyny barlamak.
3. Okuwçylaryň ünsüni sapaga gönükdirmek. 4. Syýasy wakalar bilen tanyşdyrmak.
2. Öý işiniň ýerine ýetirilişini barlamak:
1. Nähili kesimlere proporsional kesimler diýilýär?
2. Nähili figuralara meňzeş figuralar diýilýär?
3. Nähili üçburçluklara meňzeş üçburçluklar diýilýär?
4. Üçburçluklaryň meňzeşligi nähili belgilenýär?
5. Meňzeş üçburçluklaryň meýdanlary nähili gatnaşýarlar?
 3. Geçilen temany jemlemek:
3. Geçilen temany jemlemek:
Üçburçluklaryň meňzeşlik nyşanlary
4. Täze temany düşündirmek:
Temany düşündirmegiň meýilnamasy:
1. Üçburçluklaryň meňzeşlik nyşanlaryny öwretmek
2.Üçburçluklaryň meňzeşlik nyşanlaryndan gelip çykýan netijeleri öwretmek
3. Üçburçluklaryň meňzeşliginiň ikinji nyşanyny subut etmegi öwretmek
Temany öwrenmek bilen okuwçylar bilmeli:
- Üçburçluklaryň meňzeşlik nyşanlaryny bilmeli
- Üçburçluklaryň meňzeşlik nyşanlaryndan gelip çykýan netijeleri bilmeli
- Nähili üçburçluklara meňzeş üçburçluklar diýilýändigini bilmeli
Temany öwrenmek bilen okuwçylar başarmaly:
- Üçburçluklaryň meňzeşliginiň birinji nyşanyny subut etmegi başarmaly
- Üçburçluklaryň meňzeşliginiň ikinji nyşanyny subut etmegi başarmaly
- Üçburçluklaryň meňzeşliginiň üçünji nyşanyny subut etmegi başarmaly
Üçburçluklaryň meňzeşliginiň birinji nyşany
Teorema.Eger bir üçburçlugyň iki burçy degişlilikde beýleki üçburçlugyň iki burçuna deň bolsa, onda bu üçburçluklar meňzeşdirler.
1-nji netije. Deňtaraply üçburçluklar meňzeşdirler.
2-nji netije. Eger deňýanly üçburçluklaryň depesindäki ýa-da esasyndaky burçlary özara deň bolsa, onda ol üçburçluklar meňzeşdirler.
3-nji netije. Eger gönüburçly üçburçlugyň bir ýiti burçy beýleki bir gönüburçly üçburçlugyň bir ýiti burçuna deň bolsa, onda ol üçburçluklar meňzeşdirler.
Üçburçluklaryň meňzeşliginiň ikinji nyşany
Teorema. Eger bir üçburçlugyň iki tarapy beýleki üçburçlugyň iki tarapyna proporsional we bu taraplaryň arasyndaky burçlary deň bolsa, onda bu üçburçluklar meňzeşdirler.
Netije. Eger gönüburçly iki üçburçlugyň biriniň katetleri beýlekisiniň katetlerine proporsional bolsa, onda ol üçburçluklar meňzeşdirler.
Üçburçluklaryň meňzeşliginiň üçünji nyşany
Teorema. Eger bir üçburçlugyň üç tarapy beýleki üçburçlugyň üç tarapyna proporsional bolsa, onda bu üçburçluklar meňzeşdirler.
5. Geçilen temany berkitmek:
26. B burç KBH we CBA üçburçluklaryň ikisi üçin hem umumy
(okuw kitabyndaky 8-nji surat) KHB=BAC=90 bolany üçin 1-nji nyşana görä KBH~CBA. S.E.Ş.
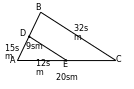 27.
27. 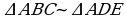 , sebäbi
, sebäbi 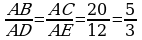 we A– umumy. Onda,
we A– umumy. Onda,
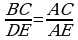 ,
,
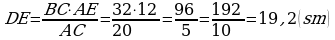 ,
,
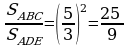 . Jogaby: 19,2sm,
. Jogaby: 19,2sm, 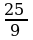 .
.
28. 1=2 we A burç umumy bolany üçin 1-nji nyşana görä ABD~ABC (okuw kitabyndaky 8-nji surat). Olaryň meňzeşliginden 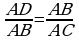 deňligi alarys.
deňligi alarys. 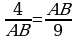 , AB2=4•9=36, AB=6.
, AB2=4•9=36, AB=6. 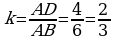 .
. 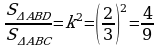 . Jogaby: 6,
. Jogaby: 6, 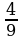 .
.
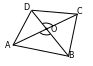 29. Subudy.
29. Subudy. 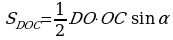
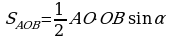 ýa–da
ýa–da
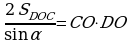 ,
, 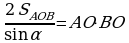 ,
,
bu deňlik sag bölekleri şerte görä deň, onda çep bölekleride deňdirler. Diýmek
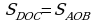 .
. 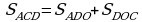 .
. 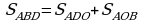
Netijede 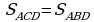 S.E.Ş.
S.E.Ş.
6. Öý işini tabşyrmak:
1. Üçburçluklaryň meňzeşliginiň birinji nyşanyny subut ediň.
2. Deňýanly üçburçluklaryň meňzeş bolmagy üçin haýsy şert ýerine ýetmeli?
3. Üçburçluklaryň meňzeşliginiň ikinji nyşanyny subut ediň.
4. Üçburçluklaryň meňzeşliginiň üçünji nyşanyny subut ediň.
5. Gönüburçly üçburçluklaryň meňzeş bolmagy üçin haýsy şert ýerine ýetmeli?
7. Sapagy jemlemek, umumylaşdyrmak, okuwçylary bahalandyrmak:
Soraglara takyk, dogry jogap beren, sapakda işjeňlik görkezip, temany gürrüň bermäge işjeň gatnaşan okuwçylar atlandyrylyp, olar bahalandyrylýar (bahalar synp žurnalyna, gündeliklere goýulýar).
Ýazan mugallym: ___________________________________________________
Bellik:________________________________________________________________
Barlan: Müdiriň okuw işleri baradaky orunbasary ____________________________
Mekdebi№:_______ Senesi: ______ _______ _______
Dersiň ady: Geometriýa Synpy:9-njy synp ______ _______ _______
| Sapagyň temasy: | 1-nji ýazuw- barlag işi |
| Sapagyň maksady. |
|
| 1) Bilim berijilik maksady: | Okuwçylaryň bilimini barlamak, pikirleniş endiklerini ösdürmek |
| 2) Terbiýeçilik maksady: | Okuwçylary watançylyk, zähmetsöýerlik, beýik adamkärçilik ruhunda terbiýelemek. Olaryň watansöýüjilik duýgularyny ösdürmek. |
| Sapagyň görnüşi: | Ýazuw-barlag işi geçirilýän sapak |
| Sapakda ulanylýan okuw-görkezme esbaplar, sanly serişdeler, paýlama maglumatlar: | Barlag iş depderleri |
Sapagyň gidişi:
1. Sapagyň guramaçylyk döwri:
1. Salamlaşmak. Gatnaşygy hasaba almak. 2. Okuwçylaryň sapaga taýýarlygyny barlamak.
3. Okuwçylaryň ünsüni sapaga gönükdirmek. 4. Syýasy wakalar bilen tanyşdyrmak.
2. Ýazuw-barlag işiniň mazmunyny düşündirmek.
Ýazuw barlag işiniň ýazgysy bilen tanyşdyrmak.
a) Sag tarap b) Cep tarap
1. a) ABC gönüburçly üçburçlugyň CD beýikligi AB gipotenuzany AD=16 sm we BD=9 sm böleklere bölýär. ACD we CBD üçburçlukla-ryň meňzeşligini subut ediň we CD beýikligi tapyň.
b) ABC gönüburçly üçburçlugyň CD beýikligi uzynlygy 9 sm bo-lan AB gipotenuzadan uzynlygy 4 sm deň bolan AD kesimi kesip alýar. ABC we ACD üçburçluklaryň meňzeşligini subut ediň we AC tapyň.
2. a) M we N nokatlar degişlilikde ABC üçburçlugyň AC we BC
taraplarynyň üstünde ýatýarlar. Eger AC=16 sm, BC=12 sm, CM=12sm, CN=9 sm bolsa, MN║AB subut ediň.
b) ABCD dörtburçlugyň AC we BD diagonallary O nokatda kesiş-ýärler. Eger AO=18 sm, OB=10 sm, OC=12 sm, OD=15 sm bolsa, ABCD dörtburçlugyň trapesiýadygyny subut ediň.
3. a) Eger AB=8 sm, BC=12 sm, AC=16 sm, KM=10 sm, MN=15 sm, KN=20 sm bolsa, ABC we KMN üçburçluklaryň meýdanlarynyň gatnaşygyny tapyň.
b) Eger PQ=16 sm, QR=20 sm, PR=28 sm, AB=12 sm, BC=15 sm, AC=21 sm bolsa, PQR we ABC üçburçluklaryň meýdanlarynyň gatna-şygyny tapyň.
3. Okuwçylar tarapyndan ýazuw-barlag işiniň ýerine ýetirilmegi.
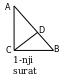 Çözülişi
Çözülişi
1. a) ACD we CBD üçburçluklaryň ikisi hem gönüburçly (1 sur.),
A+B=90 we A+ACD=90 bolany üçin B= ACD.
ADC=BDC=90 we B= ACD bolany üçin üçburçluklaryň
meňzeşliginiň 1-nji nyşanyna görä ACD we CBD üçburçluklar meňzeşdirler.
Diýmek, 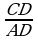 =
=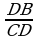 ; CD2=AD•DB; CD=
; CD2=AD•DB; CD=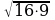 =12 (sm) alarys.
=12 (sm) alarys.
b) A ýiti burç ACD we ABC gönüburçly üçburçluklar üçin umumy (1 sur.). Diýmek, üçburçluklaryň meňzeşliginiň 1-nji nyşanyna görä ABC we ACD üçburçluklar meňzeşdirler. Bu üçburçluklaryň meňzeşliginden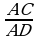 =
=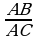 ; AC2=AD•AB; AC=
; AC2=AD•AB; AC= 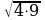 =6 (sm) alarys.
=6 (sm) alarys.
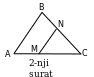 2. a)
2. a) 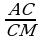 =
=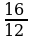
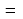
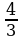 (2 sur.).
(2 sur.). 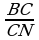 =
=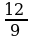 =
=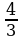 . C burç ABC we MNC
. C burç ABC we MNC
üçburçluklar üçin umumy. Diýmek, 2-nji nyşana görä ABC we MNC
üçburçluklar meňzeşdir. ABC=MNC bolany üçin iki cöni
çyzygyň parallelliginiň 2-nji nyşanyna görä MN║AB. SEŞ.
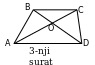 b)
b) 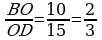 (3 sur).
(3 sur).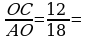
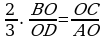 ; BOC=AOD.
; BOC=AOD.
Diýmek, 2-nyşana görä BOC~AOD. BCO=DAO. Iki göni
çyzygyň parallelliginiň 2-nji nyşana görä BC||AD.
Diýmek, ABDC trapesiýa.
3. a) 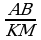 =
=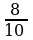
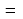
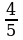 .
. 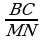 =
=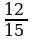
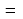
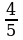 ;
; 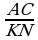 =
=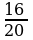
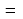
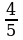 .
.
Diýmek, 3-nji nyşana görä ABC~KMN. 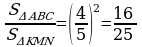 .
.
b) 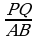 =
=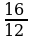
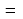
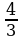 ;
; 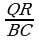 =
=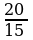
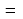
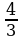 .
. 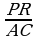 =
=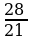
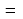
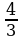 . Diýmek, 3-nji nyşana görä PQR~ABC.
. Diýmek, 3-nji nyşana görä PQR~ABC. 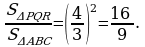
4. Sapagy jemlemek, öý işini tabşyrmak.
Okuwçylaryň depderlerini toplap almak. Sapagy umumylaşdyryp jemlemek.
Ýazan mugallym: ___________________________________________________
Bellik:________________________________________________________________
Barlan: Müdiriň okuw işleri baradaky orunbasary ____________________________
Mekdebi№:_______ Senesi: ______ _______ _______
Dersiň ady: Geometriýa Synpy:9-njy synp ______ _______ _______
| Sapagyň temasy: | Üçburçluklaryň meňzeşlik nyşanlary |
| Sapagyň maksatlary: |
|
| 1)Bilim berijilik maksady: | Üçburçluklaryň meňzeşlik nyşanlary hakynda düşünjeleri öwretmek. Okuwçylaryň öňki öwrenenlerini berkitmek, olaryň başarnyklaryny, ukyplaryny ösdürmek. |
| 2) Terbiýeçilik maksady: | Okuwçylary watançylyk, zähmetsöýerlik, beýik adamkärçilik ruhunda terbiýelemek. Olaryň watansöýüjilik duýgularyny ösdürmek. |
| Sapagyň görnüşi: | Täze maglumatlary öwretmek sapagy |
| Sapakda ulanylýan okuw-görkezme esbaplar, sanly serişdeler, paýlama maglumatlar: | Kompýuter, interaktiw tagta, slaýdlar, tanyşdyrmalar, tablisalar, tema degişli soraglar, çyzgyç. |
Sapagyň gidişi:
1. Sapagyň guramaçylyk döwri:
1. Salamlaşmak. Gatnaşygy hasaba almak. 2. Okuwçylaryň sapaga taýýarlygyny barlamak.
3. Okuwçylaryň ünsüni sapaga gönükdirmek. 4. Syýasy wakalar bilen tanyşdyrmak.
2. Öý işiniň ýerine ýetirilişini barlamak:
1. Nähili kesimlere proporsional kesimler diýilýär?
2. Nähili figuralara meňzeş figuralar diýilýär?
3. Nähili üçburçluklara meňzeş üçburçluklar diýilýär?
4. Üçburçluklaryň meňzeşligi nähili belgilenýär?
5. Meňzeş üçburçluklaryň meýdanlary nähili gatnaşýarlar?
 3. Geçilen temany jemlemek:
3. Geçilen temany jemlemek:
1-nji ýazuw- barlag işi
4. Täze temany düşündirmek:
Temany düşündirmegiň meýilnamasy:
1. Üçburçluklaryň meňzeşlik nyşanlaryny öwretmek
2.Üçburçluklaryň meňzeşlik nyşanlaryndan gelip çykýan netijeleri öwretmek
3. Üçburçluklaryň meňzeşliginiň ikinji nyşanyny subut etmegi öwretmek
Temany öwrenmek bilen okuwçylar bilmeli:
- Üçburçluklaryň meňzeşlik nyşanlaryny bilmeli
- Üçburçluklaryň meňzeşlik nyşanlaryndan gelip çykýan netijeleri bilmeli
- Nähili üçburçluklara meňzeş üçburçluklar diýilýändigini bilmeli
Temany öwrenmek bilen okuwçylar başarmaly:
- Üçburçluklaryň meňzeşliginiň birinji nyşanyny subut etmegi başarmaly
- Üçburçluklaryň meňzeşliginiň ikinji nyşanyny subut etmegi başarmaly
- Üçburçluklaryň meňzeşliginiň üçünji nyşanyny subut etmegi başarmaly
Üçburçluklaryň meňzeşliginiň birinji nyşany
Teorema.Eger bir üçburçlugyň iki burçy degişlilikde beýleki üçburçlugyň iki burçuna deň bolsa, onda bu üçburçluklar meňzeşdirler.
1-nji netije. Deňtaraply üçburçluklar meňzeşdirler.
2-nji netije. Eger deňýanly üçburçluklaryň depesindäki ýa-da esasyndaky burçlary özara deň bolsa, onda ol üçburçluklar meňzeşdirler.
3-nji netije. Eger gönüburçly üçburçlugyň bir ýiti burçy beýleki bir gönüburçly üçburçlugyň bir ýiti burçuna deň bolsa, onda ol üçburçluklar meňzeşdirler.
Üçburçluklaryň meňzeşliginiň ikinji nyşany
Teorema. Eger bir üçburçlugyň iki tarapy beýleki üçburçlugyň iki tarapyna proporsional we bu taraplaryň arasyndaky burçlary deň bolsa, onda bu üçburçluklar meňzeşdirler.
Netije. Eger gönüburçly iki üçburçlugyň biriniň katetleri beýlekisiniň katetlerine proporsional bolsa, onda ol üçburçluklar meňzeşdirler.
Üçburçluklaryň meňzeşliginiň üçünji nyşany
Teorema. Eger bir üçburçlugyň üç tarapy beýleki üçburçlugyň üç tarapyna proporsional bolsa, onda bu üçburçluklar meňzeşdirler.
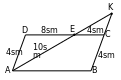 5. Täze temany berkitmek:
5. Täze temany berkitmek:
30. a) 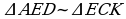 bolany üçin
bolany üçin
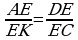 ,
, 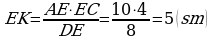
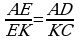 ,
, 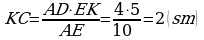
b) önki bölümçä meňzeş çözülýär.
31. a) DOC=AOB (wertikal burçlar). AB║DC we AC
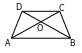 kesiji çyzyk bolany üçin DCO=OAB (atanak ýatýan burçlar).
kesiji çyzyk bolany üçin DCO=OAB (atanak ýatýan burçlar).
Diýmek, 1-nji nyşana görä DOC~AOB.
Meňzeş taraplar bolany üçin
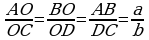 .
.
Jogaby: 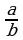 .
.
b) AB:DC=AO:OC=(AC-OC):OC. AB:DC=9,6dm:24sm=4,
4=(15-OC):OC, 4•OC=15-OC, OC=3sm, AO=15-3=12sm. Jogaby: 12sm
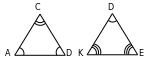 32. a) Deň ýiti burçy bolanda hemişe deňýanly üçburçluklar meňzeş bolup bilmez. Meselem. Bir deňýanly üçburçlugyň esasyndaky ýiti burçuna
32. a) Deň ýiti burçy bolanda hemişe deňýanly üçburçluklar meňzeş bolup bilmez. Meselem. Bir deňýanly üçburçlugyň esasyndaky ýiti burçuna
beýleki deňýanly
üçburçlugyň esasynyň
garşysyndaky burçy
deň bolan ýagdaýynda
bu iki deňyanly üçburçluk
meňzeş bolup bilmezler. A=B=D bolan ýagdaý.
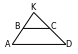 b) we ç) bölümçeler üçin iki deňýanly üçburçluklar hemişe meňzeş bolarlar. Bu ýagdaýda deňýanly üçburçlugyň esasynyň garşysyndaky burç kütek, ýa–da gönüburç bolup biler, galan burçlar hem özara deň bolar. Diýmek üçburçluklar meňzeşdirler.
b) we ç) bölümçeler üçin iki deňýanly üçburçluklar hemişe meňzeş bolarlar. Bu ýagdaýda deňýanly üçburçlugyň esasynyň garşysyndaky burç kütek, ýa–da gönüburç bolup biler, galan burçlar hem özara deň bolar. Diýmek üçburçluklar meňzeşdirler.
33. KBC~KAD. AD:BC=AK:BK. 8:5=(3,6+BK):KB; KB=6sm.
AD:BC=KD:KC; 8:5=(3,9+KC):KC. KC=6,5sm. Jogaby: 6sm, 6,5sm.
6. Öý işini tabşyrmak:
1. Üçburçluklaryň meňzeşliginiň birinji nyşanyny subut ediň.
2. Deňýanly üçburçluklaryň meňzeş bolmagy üçin haýsy şert ýerine ýetmeli?
3. Üçburçluklaryň meňzeşliginiň ikinji nyşanyny subut ediň.
4. Üçburçluklaryň meňzeşliginiň üçünji nyşanyny subut ediň.
5. Gönüburçly üçburçluklaryň meňzeş bolmagy üçin haýsy şert ýerine ýetmeli?
7. Sapagy jemlemek, umumylaşdyrmak, okuwçylary bahalandyrmak:
Soraglara takyk, dogry jogap beren, sapakda işjeňlik görkezip, temany gürrüň bermäge işjeň gatnaşan okuwçylar atlandyrylyp, olar bahalandyrylýar (bahalar synp žurnalyna, gündeliklere goýulýar).
Ýazan mugallym: ___________________________________________________
Bellik:________________________________________________________________
Barlan: Müdiriň okuw işleri baradaky orunbasary ____________________________





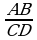 aýdylýar. Eger
aýdylýar. Eger 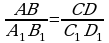 bolsa, onda AB we CD kesimler A1B1 we C1D1 kesimlere proporsional kesimler diýilýär. Mysal üçin, uzynlyklary 2 sm we 1 sm bolan AB we CD kesimler uzynlyklary 3 sm we 1,5 sm bolan А1В1 we С1D1 kesimlere proporsionaldyr. Sebäbi
bolsa, onda AB we CD kesimler A1B1 we C1D1 kesimlere proporsional kesimler diýilýär. Mysal üçin, uzynlyklary 2 sm we 1 sm bolan AB we CD kesimler uzynlyklary 3 sm we 1,5 sm bolan А1В1 we С1D1 kesimlere proporsionaldyr. Sebäbi 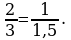
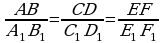 şert ýerine ýetse, onda AB, CD we EF üç kesim, degişlilikde A1B1, C1D1 we E1F1 üç kesime proporsionaldyr.
şert ýerine ýetse, onda AB, CD we EF üç kesim, degişlilikde A1B1, C1D1 we E1F1 üç kesime proporsionaldyr.
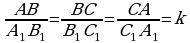 bolsa, onda ABC we A1B1C1 üçburçluklara meňzeş üçburçluklar diýilýär.
bolsa, onda ABC we A1B1C1 üçburçluklara meňzeş üçburçluklar diýilýär.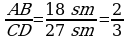
 Eger bu kesimleriň uzynlyklary santimetrlerde dälde millimetrlerde aňladylsa, bu gatnaşyk üýtgemez.
Eger bu kesimleriň uzynlyklary santimetrlerde dälde millimetrlerde aňladylsa, bu gatnaşyk üýtgemez.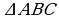 -yň
-yň 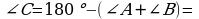
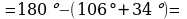
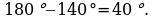
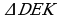 -yň
-yň 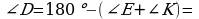
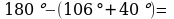
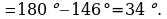

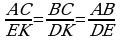 ýa-da
ýa-da 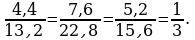
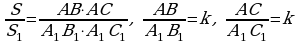 bolany üçin,
bolany üçin, 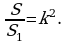 Teorema subut edildi.
Teorema subut edildi.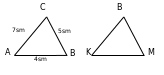 5. Täze temany berkitmek:
5. Täze temany berkitmek: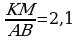 ,
, 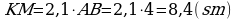
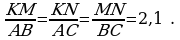
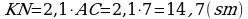
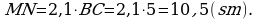
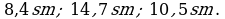
 6. Subudy. ABC~KMN bolsun, onda
6. Subudy. ABC~KMN bolsun, onda 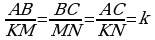
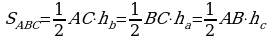
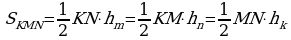
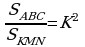 ýa–da
ýa–da 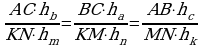
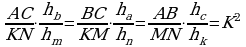 (*)
(*) emma
emma 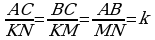 bolany üçin (*) deňligi K bölüp alarys:
bolany üçin (*) deňligi K bölüp alarys: 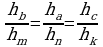 Subut etmeli hem şudy.
Subut etmeli hem şudy.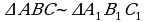 bolany üçin
bolany üçin 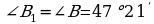 deň bolar.
deň bolar.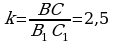
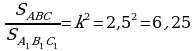
 2-nji teorema. Üçburçlugyň bissektrisasy garşysyndaky tarapy sep leşýän taraplara proporsional bolan kesimlere bölýär.
2-nji teorema. Üçburçlugyň bissektrisasy garşysyndaky tarapy sep leşýän taraplara proporsional bolan kesimlere bölýär.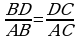 bolýandygyny subut edeliň. ABD we ACD üçburçluklaryň umumy AH beýikligi bolany üçin:
bolýandygyny subut edeliň. ABD we ACD üçburçluklaryň umumy AH beýikligi bolany üçin: 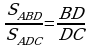 (1)
(1)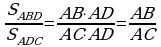 (2)
(2) 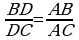 ýa-da
ýa-da 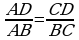 ,
, 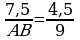 .
.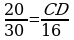 alarys. CD=16•
alarys. CD=16•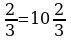 sm. Jogaby:
sm. Jogaby: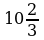 sm.
sm. 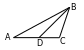 8. AC=AD+DC=7,5+2,5=10sm.
8. AC=AD+DC=7,5+2,5=10sm. 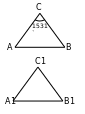 9.
9. 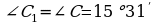 deň bolar.
deň bolar.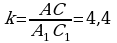 deňdir. Onda
deňdir. Onda 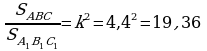 ,
,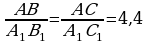 ýa–da
ýa–da 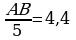 , AB=22sm.
, AB=22sm.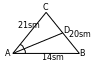 11. Üçburçlugyň bissektrisasynyň
11. Üçburçlugyň bissektrisasynyň 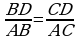 ýa–da
ýa–da 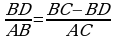
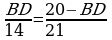 ,
, 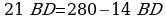 ,
, 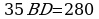 ,
, 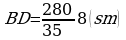 .
. 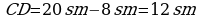 . Jogaby: 8sm; 12sm.
. Jogaby: 8sm; 12sm. 3. Geçilen temany jemlemek:
3. Geçilen temany jemlemek: 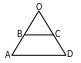 23.
23. 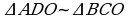 bolany üçin alarys:
bolany üçin alarys: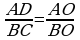 ,
, 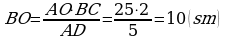
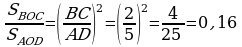

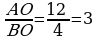 ;
; 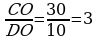
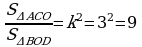 .
.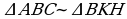 , sebäbi
, sebäbi 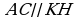 .
. 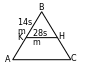 Onda
Onda 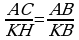 ,
, 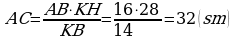
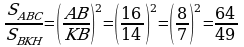 .
.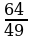 .
.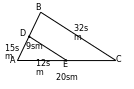 27.
27. 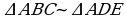 , sebäbi
, sebäbi 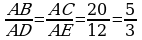 we A– umumy. Onda,
we A– umumy. Onda, 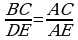 ,
, 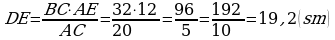 ,
,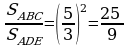 . Jogaby: 19,2sm,
. Jogaby: 19,2sm, 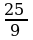 .
.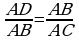 deňligi alarys.
deňligi alarys. 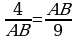 , AB2=4•9=36, AB=6.
, AB2=4•9=36, AB=6. 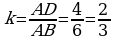 .
. 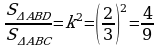 . Jogaby: 6,
. Jogaby: 6, 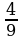 .
. 29. Subudy.
29. Subudy. 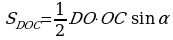
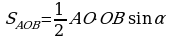 ýa–da
ýa–da 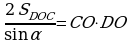 ,
, 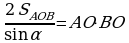 ,
, 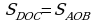 .
. 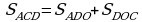 .
. 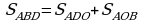
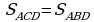 S.E.Ş.
S.E.Ş.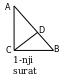 Çözülişi
Çözülişi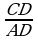 =
=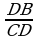 ; CD2=AD•DB; CD=
; CD2=AD•DB; CD=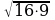 =12 (sm) alarys.
=12 (sm) alarys.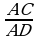 =
=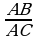 ; AC2=AD•AB; AC=
; AC2=AD•AB; AC= 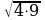 =6 (sm) alarys.
=6 (sm) alarys.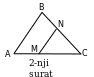 2. a)
2. a) 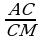 =
=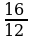
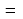
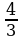 (2 sur.).
(2 sur.). 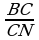 =
=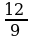 =
=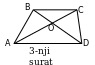 b)
b) 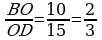 (3 sur).
(3 sur).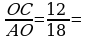
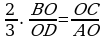 ; BOC=AOD.
; BOC=AOD.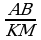 =
=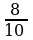
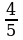 .
. 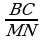 =
=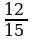
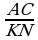 =
=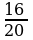
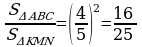 .
. 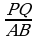 =
=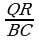 =
=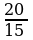
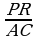 =
=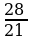
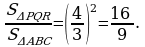
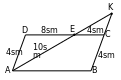 5. Täze temany berkitmek:
5. Täze temany berkitmek: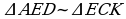 bolany üçin
bolany üçin 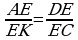 ,
, 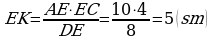
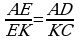 ,
, 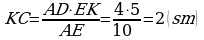
 kesiji çyzyk bolany üçin DCO=OAB (atanak ýatýan burçlar).
kesiji çyzyk bolany üçin DCO=OAB (atanak ýatýan burçlar).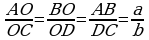 .
.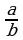 .
. 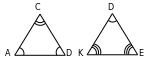 32. a) Deň ýiti burçy bolanda hemişe deňýanly üçburçluklar meňzeş bolup bilmez. Meselem. Bir deňýanly üçburçlugyň esasyndaky ýiti burçuna
32. a) Deň ýiti burçy bolanda hemişe deňýanly üçburçluklar meňzeş bolup bilmez. Meselem. Bir deňýanly üçburçlugyň esasyndaky ýiti burçuna 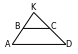 b) we ç) bölümçeler üçin iki deňýanly üçburçluklar hemişe meňzeş bolarlar. Bu ýagdaýda deňýanly üçburçlugyň esasynyň garşysyndaky burç kütek, ýa–da gönüburç bolup biler, galan burçlar hem özara deň bolar. Diýmek üçburçluklar meňzeşdirler.
b) we ç) bölümçeler üçin iki deňýanly üçburçluklar hemişe meňzeş bolarlar. Bu ýagdaýda deňýanly üçburçlugyň esasynyň garşysyndaky burç kütek, ýa–da gönüburç bolup biler, galan burçlar hem özara deň bolar. Diýmek üçburçluklar meňzeşdirler.









