Конспект урока "Числовые выражения"

Тема: «Числовые выражения».

        7 класс

Цели урока:

• закрепление умений и навыков сложения, вычитания, умножения и деления положительных и отрицательных чисел;

• формирование ответственности, организованности, дисциплинированности учащихся;

Оформление: плакаты с портретами ученых, на доске слова:

Наша задача – помочь вам овладеть

алгебраическими методами;

ваша задача – не противиться обучению,

с готовностью следовать за нами,

преодолевая трудности.

А. Мордкович

Оборудование: учебники и задачники «Алгебра 7», таблица квадратов, выставка книг.

ХОД УРОКА

1. Что изучает алгебра? (Диалог учителя (У) и одного из учеников (А).)

У. Какой предмет вы изучали в прошлом году?

А. Математику.

У. Есть о математике молва,

     Что она в порядок ум приводит.

     Поэтому хорошие слова

     Часто говорят о ней в народе.

Чем вы занимались на уроках математики?

А. Проводили вычисления с целыми и дробными числами, решали уравнения, задачи, строили фигуры в координатной плоскости и т. д.

У. Все это составляло содержание предмета «Математика». Этот предмет подразделяется на огромное число самостоятельных дисциплин: алгебру, геометрию, теорию вероятностей, математический анализ, теорию игр и т. д. Мы приступаем к изучению алгебры. Вы уже дома познакомились с учебником. Чем он отличается, например, от учебника литературы?

А. В нем много цифр и букв, причем букв латинских.

У. Вы знаете, что 2+3=3+2. Сформулируйте словами известное вам свойство сложения.

А. От перестановки слагаемых сумма не изменяется.

У. Можно записать короче: a+b=b+a. Таким образом, буквы помогают записывать свойства действий над числами в удобной для запоминания форме. Говорят: «Высказанное утверждение записано на математическом языке». Вспомните, как найти расстояние, зная скорость и время.

А. Чтобы найти расстояние, надо скорость умножить на время.

У. Запишем короче: s=vt. То есть буквы помогают записать в виде формул правила для нахождения значений интересующих нас величин. Чем еще отличается алгебра, например, от арифметики? В арифметических задачах по известным правилам находят неизвестное число. В алгебре неизвестную величину обозначают буквой. Эта неизвестная величина и данные в условии задачи связываются между собой уравнением, из решения которого и находится неизвестная величина. Отдельные алгебраические понятия и приемы решения задач возникли несколько тысяч лет назад в древних государствах – Вавилоне и Египте. О состоянии математических знаний в те века можно судить по древним рукописям (папирусам), найденным на местах древних городов.

В 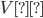І в. до н.э. греки усвоили достижения египтян в математике. В начале ІX в. (830г.) хорезмийский ученый Мухаммед-бен-Муса ал-Хорезми написал книгу «Хисаб алджебр вал-Мукабала» («Метод восстановления и противопоставления») – это была первая книга по алгебре. В ней он впервые рассмотрел методы и приемы алгебры. С момента написания этой книги алгебра становиться самостоятельной наукой. Само слово «алгебра» произошло, вероятно, от слова «алджебр», что означает «восстановление». Словом «алгебра» в арабском языке называлось искусство врача восстанавливать сломанную руку или ногу. Хирурга у арабов называют алгебраистом. Таким образом, математика позаимствовала это слово из медицины.

Дальнейшее развитие алгебры происходило в основном в Индии (до XІІ в.) и в Средней Азии (до XV в.). Ученые ал-Бируни (X в.), Омар Хайям (XІ в.), ал-Каши (XV в.) сделали много важных открытий в алгебре. В XІІІ – XVІ в. в Италии жили выдающиеся математики: Леонардо Пизанский, Кордано, Тарталья и др., которые открыли много ценного для этой науки. Алгебру до XVІІ в. условно называли риторической (словесной). Дело в том, что когда не существовало единых условных знаков «+», «», «a²» и многих других, которые используем мы. Условие задачи, все действия и ответ записывали полностью словами. Для удобства запоминания иногда эта запись делалась в стихах. Математические символы вводились постепенно. Так знак равенства «=» введен английским ученым Р. Рикордом в 1557 г., знаки «:» и «» - немецким математиком Лейбницем в конце XVІІ в., скобки – в конце XVІ в. Математические символы дали возможность ученым разных стран понять друг друга. В формировании алгебры как науки большие заслуги принадлежат французским ученым Франсуа Виету и Рене Декарту. В течение XVІІІ – XX в. из алгебры выросли новые математические науки: алгебра многочленов, векторная алгебра и т.д. Науки эти изучаются в высшей школе.

В школьной алгебре задачи решают путем составления уравнений, изучают сами уравнения, связи между величинами (некоторые из этих связей называют функциями). При этом используются буквы, выражения с буквами подвергаются различным преобразованиям (тождественным преобразованиям). Но за всеми этими буквами чаще всего скрываются числа.

…Предчувствие разоблачает тайны,

Проводником нелицемерным светит;

Едва откроется намек случайный,

Объемлет вас не предсказанный трепет,

Вам поклоняюсь, вас желаю, числа!

Свободные, бесплотные, как тени,

Вы радугой связующей повисли

К раздумьям с вершины вдохновенья.

В. Брюсов

Иногда говорят: «Алгебра держится на четырех китах: на уравнении, числе, тождестве, функции». Алгебра, к изучению которой мы приступаем, дает человеку возможность не только выполнять различные вычисления, но и учит его делать это как можно быстрее, рациональнее.

1. Рассмотрение нового материала.

У. Из чего составлена запись 3+5=7?

А. Из чисел и знаков арифметических действий.

У. Запись, составленную из чисел и знаков арифметических действий, называют числовым выражением: 3+57 – числовое выражение, тогда как       3+5+5 : +  - бессмысленный набор символов. На странице 10 учебника найдите это правило и прочитайте его.

(Ученики находят правило в тексте учебника и один из них читает его вслух).

У. На уроках математики мы занимались упрощениями числовых выражений. Вспомним, как это делается. Для этого разберем пример 1 из учебника.

Какие математические факты вам пришлось вспомнить, разбирая этот пример?

(Ученики называют математические факты, затем зачитывают их со страницы 12 учебника).

У. Какое число получилось в результате?

А. .

У. Число, которое получается в результате упрощения числового выражения, называют значением числового выражения. Найдите это правило на странице 13 учебника, прочитайте его.

1. Устный счет.

У. Откройте страницу 4 задачника; выполняя упражнения 1 и 3, прочитайте выражения, найдите их значения, проговорите соответствующие правила действий с положительными и отрицательными числами.

1. Закрепление изученного материала.

У. Упражнение 4 решаем на доске и в тетрадях. Находя значения числовых выражений, проговаривайте правила действий с обыкновенными дробями.

(Правило рассказывает ученик, выполняющий упражнение на доске. Затем применяется метод хорового повторения, что способствует развитию грамотной математической речи, запоминанию правил и усвоению материала учащимися.)

4.а) 

                                     1) 

                                     2) 

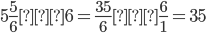
Ответы: б) ;  в) ; г) 15.

10. (У доски работают 4 ученика.)

а) + 1 =  = 2+4=6 (переместительный и сочетательный законы сложения);

б) (15+2)(14+3)=1717=289 (переместительный и сочетательный законы умножения);

в)  (распределительный закон умножения относительно сложения);

г) 

15. а) 1

1. Подведение итога урока.

• Какую тему вы изучили?

• Что называется числовым выражением?

• Что называется значением числового выражения?

• Какие математические факты используют в процессе решения примеров?