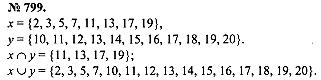Конспект урока по алгебре 8 класс

Класс: 8

Предмет: алгебра

Тема урока: Пересечение и объединение множеств (к УМК Макарычева)

Цели:

• Образовательные: познакомиться с понятиями множества, элементов множества, пересечения и объединения множеств, пустого множества; научиться находить в несложны ситуациях пересечение и объединение множеств; иллюстрировать с помощью кругов Эйлера соотношение между некоторыми множествами.

• Развивающие: развитие навыков анализа, синтеза, обобщения, умения размышлять, аргументировать, воспроизводить информацию, формирование грамотной математической речи.

• Воспитательные: развитие коммуникативных навыков (умения работать в группе, слушать и слышать, понимать и принимать; толерантность, тактичность, коммуникабельность, самокритичность); навыков самостоятельной работы, самоконтроля;

• Здоровьесбережения: создание благоприятной эмоциональной атмосферы, поддержка общего позитивного фона занятий; создание ситуации успеха для каждого ученика.

1. Организационный момент

Приветствие обучающихся, проверка их готовности к уроку (наличие учебников, тетрадей, дневников), фиксация отсутствующих. Объявление общей цели урока и плана его проведения, способа оценивания знаний и умений учащихся на уроке.

Флипчарт (страница 2)

1. Мотивация (самоопределение) к учебной деятельности

Флипчарт (страница 4)

Попробуйте решить задачу:

Сегодня мы изучим достаточно простой способ решения подобных задач. Для этого нам необходимо познакомиться еще с некоторыми математическими понятиями и способами действий, которые в дальнейшем будут нам необходимы.

1. Изучение нового материала

1. Пересечение и объединение множеств

1 задание (флипчарт – стр. 5).

Есть ли признак, по которому объекты, изображенные на доске, можно разделить на группы? Какой? Разделите их на группы «Овощи» и «Фрукты» (убрать синие фигуры с надписей).

(Группы элементов обрисовать кругом)

Какие синонимы вы можете подобрать к слову «группа»?

В математике такие группы называют «множествами». Попробуйте сформулировать определение множества. (Множество – это совокупность (или набор) объектов, объединенных между собой по какому-либо признаку (признакам)). Основатель теории множеств, немецкий математик Георг Кантор (1845 - 1918), выразил определение следующим образом: «Множество есть многое, мыслимое как единое целое» - (флипчарт – стр. 6).

Объекты, из которых состоит множество, называются элементами множества. Обозначение множества, известных числовых множеств.

Назовите какие-либо известные вам множества из жизни, из математики или других школьных предметов. Сколько элементов может содержать множество?

В задании 1 выберите множество «Мебель». Сколько элементов в этом множестве? Такое множество называют «пустым». Обозначение ø.

2 задание (флипчарт – стр. 7).

Выделите из предметов, изображенных на доске, множества «Синие» и «Транспорт».

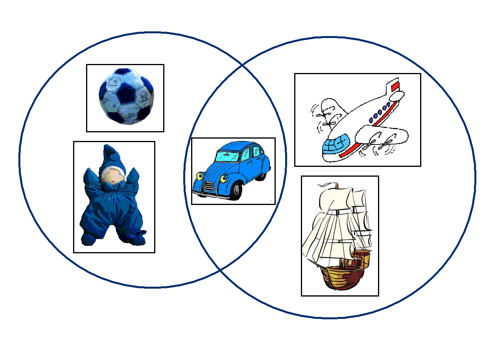
Получили предмет, который можно отнести и к множеству «Синие», и к множеству «Транспорт» (обвести в пересекающиеся круги). Т. о. мы получили пересечение множеств. Попробуйте дать определение пересечению множеств. Сравните это определение с определением в учебнике. Верно ли было наше определение?

Обозначение пересечения множеств.

3 задание (флипчарт – стр. 8)

Выделите из предметов, изображенных на доске, множества «Неживое» и «Транспорт».

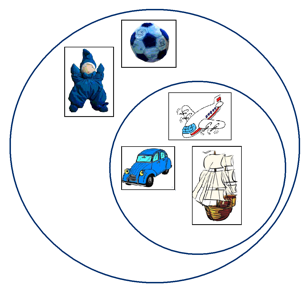
Т. о. мы получили объединение множеств (обвести в единый круг). Попробуйте дать определение объединению множеств. Сравните это определение с определением в учебнике. Верно ли было наше определение?

Обозначение объединения множеств.

2. Способы задания множества (флипчарт – стр. 9)

3. Круги Эйлера (флипчарт – стр. 10)

Круги, которыми я выделяла на доске множества в заданиях 1 – 3, называются Кругами Эйлера.

Они бывают очень удобны для изображения множеств и решения задач на множества, например, задачи, которую мы пытались решить в начале урока, до изучения новой темы:

1. Физминутка

Упражнение для глаз: «жмурки» - сильно зажмуриться, а потом широко раскрыть глаза (5 раз)

1. Первичное закрепление нового материала с проговариванием во внешней речи

№ 799, № 801 (а, б), № 806, № 807

Решение № 799 обучающимися у доски с обсуждением решения.

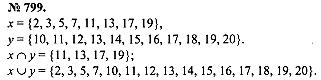
№ 801 (а,б) два человека решают с обратной стороны доски, остальные самостоятельно в тетради, после чего – самопроверка.

Решение № 806 обучающимися у доски с обсуждением решения.

№ 807 – работа в парах

1. Включение нового знания в систему знаний и повторение

Флипчарт – стр. 11.

1. Домашнее задание

Инструктаж к домашнему заданию

П. 32, № 801 (в), № 805, повт. п. 10, 11

Дополнительная задача (для желающих) - флипчарт – стр. 12:

Из 100 отдыхающих на турбазе «Озеро Графское» 30 детей - отличники учебы, 28 - участники олимпиад, 42 - спортсмены. Кроме того, 8 учащихся одновременно являются участниками олимпиад и спортсменами, 10 – участники олимпиад и отличники, 5 – спортсмены и отличники учебы, 3 – и отличники, и участники олимпиад, и спортсмены. Сколько отдыхающих не относятся ни к одной из групп?

1. Рефлексия

Все ли цели урока достигнуты? (флипчарт – стр. 3)

Флипчарт – стр. 13.

1. Итоги урока

Обсуждение и выставление отметок за урок

Дополнительная задача:

Из 100 отдыхающих на турбазе «Озеро Графское» 30 детей - отличники учебы, 28 - участники олимпиад, 42 - спортсмены. Кроме того, 8 учащихся одновременно являются участниками олимпиад и спортсменами, 10 – участники олимпиад и отличники, 5 – спортсмены и отличники учебы, 3 – и отличники, и участники олимпиад, и спортсмены. Сколько отдыхающих не относятся ни к одной из групп?

Дополнительная задача:

Из 100 отдыхающих на турбазе «Озеро Графское» 30 детей - отличники учебы, 28 - участники олимпиад, 42 - спортсмены. Кроме того, 8 учащихся одновременно являются участниками олимпиад и спортсменами, 10 – участники олимпиад и отличники, 5 – спортсмены и отличники учебы, 3 – и отличники, и участники олимпиад, и спортсмены. Сколько отдыхающих не относятся ни к одной из групп?

Дополнительная задача:

Из 100 отдыхающих на турбазе «Озеро Графское» 30 детей - отличники учебы, 28 - участники олимпиад, 42 - спортсмены. Кроме того, 8 учащихся одновременно являются участниками олимпиад и спортсменами, 10 – участники олимпиад и отличники, 5 – спортсмены и отличники учебы, 3 – и отличники, и участники олимпиад, и спортсмены. Сколько отдыхающих не относятся ни к одной из групп?

Дополнительная задача:

Из 100 отдыхающих на турбазе «Озеро Графское» 30 детей - отличники учебы, 28 - участники олимпиад, 42 - спортсмены. Кроме того, 8 учащихся одновременно являются участниками олимпиад и спортсменами, 10 – участники олимпиад и отличники, 5 – спортсмены и отличники учебы, 3 – и отличники, и участники олимпиад, и спортсмены. Сколько отдыхающих не относятся ни к одной из групп?

Дополнительная задача:

Из 100 отдыхающих на турбазе «Озеро Графское» 30 детей - отличники учебы, 28 - участники олимпиад, 42 - спортсмены. Кроме того, 8 учащихся одновременно являются участниками олимпиад и спортсменами, 10 – участники олимпиад и отличники, 5 – спортсмены и отличники учебы, 3 – и отличники, и участники олимпиад, и спортсмены. Сколько отдыхающих не относятся ни к одной из групп?

Дополнительная задача:

Из 100 отдыхающих на турбазе «Озеро Графское» 30 детей - отличники учебы, 28 - участники олимпиад, 42 - спортсмены. Кроме того, 8 учащихся одновременно являются участниками олимпиад и спортсменами, 10 – участники олимпиад и отличники, 5 – спортсмены и отличники учебы, 3 – и отличники, и участники олимпиад, и спортсмены. Сколько отдыхающих не относятся ни к одной из групп?

Дополнительная задача:

Из 100 отдыхающих на турбазе «Озеро Графское» 30 детей - отличники учебы, 28 - участники олимпиад, 42 - спортсмены. Кроме того, 8 учащихся одновременно являются участниками олимпиад и спортсменами, 10 – участники олимпиад и отличники, 5 – спортсмены и отличники учебы, 3 – и отличники, и участники олимпиад, и спортсмены. Сколько отдыхающих не относятся ни к одной из групп?