| 2.Актуализация изученных знаний.
| 20 мин | - Ответьте на следующие вопросы: - Что называется вектором?
- Как обозначается и изображается вектор?
- Кто желает выйти к доске и изобразить вектор? - Какой вектор называется нулевым? - Дайте определение длины (модуля) вектора.
- Сформулируйте определение коллинеарных векторов.
- Что вы можете сказать про нулевой вектор? - Какие вектора называются сонаправленными?
- Сформулируйте определение противоположнонаправленных векторов. - Какие векторы называются равными?
- Теорию мы с вами вспомнили, теперь перейдем к практическим заданиям, работа в парах, время выполнения – 10 минут (раздаются на каждую парту карточки с заданиями (см. приложение)). - Давайте сравнимся с ответами. По очереди каждая пара разбирает по заданию и говорит ответ, если нужно что-то построить – выходит к доске.
|
- отрезок, для которого указано, какая из его граничных точек считается началом, а какая – концом, называется направленным отрезком или вектором. - обозначается двумя заглавными латинскими буквами со стрелкой над ними или одной строчной буквой. К доске выходит один учащийся. - начало вектора совпадает с его концом. - длиной или модулем ненулевого вектора 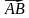 называется длина отрезка AB. называется длина отрезка AB. - ненулевые векторы называются коллинеальными, если лежат на одной прямой либо на параллельных прямых. - Нулевой вектор считается коллинеарным любому вектору.
- ненулевые коллинеарные векторы, имеющие одинаковое направление. - ненулевые коллинеарные векторы, имеющие противоположное направление. - Векторы называются равными, если они сонаправлены и их длины равны. Выполняют задания.
По очереди разбирают задания. |
| 4. Постановка проблемы. Переход к новому материалу. | 10 мин | - Запишите в тетрадях тему нашего урока «Откладывание вектора от данной точки». - На доске изображено три вектора (изображены разными цветами) и имеется точка М. Требуется от данной точки отложить векторы, равные данным.   B E B E
A F   C M C M
D - Что нам нужно сделать, чтобы отложить от т. М вектор 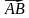 ? ?
На доске откладывает вектор от данной точки. - Отложим таким же образом векторы 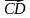 и и  . Кто желает выйти к доске? . Кто желает выйти к доске? - Что нам нужно сделать, чтобы отложить вектор от данной точки? - А если т. М точка прямой АВ, то каким образом мы отложим от нее данный вектор? Построим его на доске.
- Отложим еще один вектор 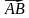 от т. М, что мы видим? Какой вывод можем сделать? от т. М, что мы видим? Какой вывод можем сделать?
- Итак, запишем определение. От любой точки М можно отложить вектор, равный данному вектору 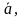 и притом только один. и притом только один. | Записывают тему.
Высказывают свои идеи. - Проведем прямую p через т. М, параллельно 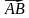 . Отложим на прямой отрезок равный . Отложим на прямой отрезок равный 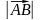 . .
К доске выходит один учащийся.
Высказывают идеи. Высказывают идеи.
- Что вектора накладываются друг на друга, значит, мы можем от данной точки отложить единственный вектор. |
| 6. Рефлексия | 3 мин | - Какую тему мы изучили сегодня на уроке? - От любой ли точки можно отложить вектор, равный данному? - Сколько векторов, равному данному вектору, можно отложить от одной точки? - Что нужно сделать, чтобы отложить вектор от данной точки?
| Отвечают на вопросы |






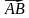 называется длина отрезка AB.
называется длина отрезка AB.
 B E
B E
 C M
C M  и
и  . Кто желает выйти к доске?
. Кто желает выйти к доске?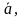 и притом только один.
и притом только один.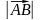 .
.









