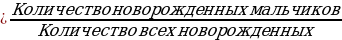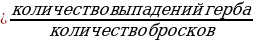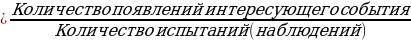Конспект урока по теме "Частота и вероятность случайного события"

Деятельность учителя

Деятельность учеников

1.Организационный момент

Здравствуйте, ребята! Сегодня на уроке вам понадобится тетрадь, учебник и ручка. Проверьте чтобы у всех было все необходимое. Теперь отметим отсутствующих.

Здороваются.

Называют отсутствующих.

2. Проверка домашнего задания

-Теперь, мы проверим с вами домашнее задание

Есть ли у вас вопросы по домашней работе?

-Хорошо
1) Тогда, вспомним, что изучает комбинаторика?

2) кто может назвать правило суммы?

3) кто может назвать правило произведения?

Все молодцы!

Нет

Комбинаторика – раздел математики, который изучает задачи выбора и расположения элементов из некоторого основного множества в соответствии с заданными правилами.

Если множество A состоит из m элементов,

а множество B — из k элементов, причем эти множества не имеют

общих элементов, то выбор «a или b», где a ∈ A, b ∈ B, можно

осуществить m+k способами.

Если элемент a можно выбрать

m способами и после каждого такого выбора элемент b можно выбрать k способами, то выбор «a и b» в указанном порядке можно

осуществить mk способами.

3. Актуализация знаний

Давайте теперь решим задачу у доски.

Из 30 участников собрания надо выбрать председателя и секретаря. Сколькими способами это можно сделать? (30*29=870 способов)

Сколько четырехзначных чисел, в которых нет одинаковых цифр, можно составить из цифр: 1, 3, 5, 7, 9?

Ученик выходит к доске решать задание с объяснением. Остальные слушают и задают возникающие вопросы

30*29=870 способов

5*4*3*2=120 чисел

4.Объяснение нового материала

Тема нашего урока «Частота и вероятность случайного события». Пожалуйста, запишите тему себе в тетрадь.

Купив лотерейный билет, мы можем выиграть, а можем не выиграть; завтра на уроке математики вас могут вызвать к доске, а могут и не вызвать. Все эти события, можно назвать какими?

Результат наблюдения, опыта, эксперимента будем называть событием.

Как правило, наблюдения или эксперимент определяются каким-то комплексом условий.

Случайным событием называют такой результат наблюдения или эксперимента, который при соблюдении данного комплекса условий может произойти, а может и не произойти.

Можно привести и другие примеры. Будет ли завтра снег, никому наверняка неизвестно, даже бюро погоды ошибается. Учитель не знает, сколько ошибок сделает школьник в контрольной работе. Приведите пожалуйста свои примеры.

В повседневной жизни в разговоре часто используется слово «вероятность», например: «это невероятный случай», «вероятнее всего будет дождь» и т.д. Здесь интуитивно оценивается возможность того или иного события, исходя из здравого смысла, интуиции. Например, мы заранее знаем, что на мультфильм пойдет больше детей, чем взрослых.

Представим, что выпущен 1 000 000 лотерейных билетов и разыгрывается один автомобиль. Можно ли, приобретя один лотерейный билет, выиграть этот приз? Конечно, можно, хотя это событие маловероятно. А если будут разыгрываться 10 автомобилей? Ясно, что вероятность выигрыша увеличится. Если же представить, что разыгрываются 999999 автомобилей, то вероятность выигрыша станет намного большей.

Следовательно, вероятности случайных событий можно сравнивать. Однако для этого следует договориться, каким образом количественно оценивать возможность появления того или иного

события.

Основанием для такой количественной оценки могут быть результаты многочисленных наблюдений или экспериментов. Так, люди давно заметили, что многие события происходят с той или

иной, на удивление постоянной, частотой.

Демографам хорошо известно число 0,512. Статистические данные, полученные в разные времена и в разных странах, свидетельствуют о том, что на 1000 новорожденных приходится в среднем 512 мальчиков. Число 0,512 называют частотой случайного события «рождение мальчика». Оно определяется формулой:

Частота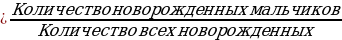

Подчеркнем, что это число получено в результате анализа многих наблюдений. В таких случаях говорят, что вероятность события «рождение мальчика» приблизительно равна 0,512.

Чтобы детальнее ознакомиться с понятием вероятности случайного события, обратимся к классическому примеру с подбрасыванием монеты.

Предположим, что в результате двух подбрасываний монеты дважды выпал герб. Тогда в данной серии, состоящей из двух испытаний, частота выпадения гербА равна:

Частота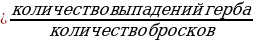

Означает ли это, что вероятность выпадения герба равна 1?

Конечно, нет.

Для того чтобы по частоте случайного события можно было оценивать его вероятность, количество испытаний должно быть достаточно большим.

Начиная с ХVІІІ в. многие исследователи проводили серии испытаний с подбрасыванием монеты.

В таблице в учебнике на странице 161 (218) приведены результаты некоторых таких испытаний. Посмотрите пожалуйста.

(рассматриваем таблицу)

По приведенным данным прослеживается закономерность: при многократном подбрасывании монеты частота выпадения герба незначительно отклоняется от числа 0,5.

Следовательно, можно считать, что вероятность случайного события «выпадение герба» приблизительно равна 0,5.

В каждом из рассмотренных примеров использовалось понятие частота случайного события. Эту величину мы вычисляли по формуле:

Частота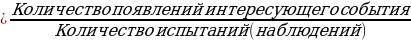

Запишите эту формулу в тетрадь

Таким образом, частота случайного события позволяет лишь приближенно оценить вероятность случайного события. Чем больше испытаний провести, тем точнее будет оценка вероятности

случайного события по его частоте.

Такую оценку вероятности случайного события называют статистической. Ее используют в разных областях деятельности человека: физике, химии, биологии, страховом бизнесе, социологии,

экономике, здравоохранении, спорте и т. д.

Вероятность случайного события обозначают буквой P (первой буквой французского слова probabilitе́— вероятность). Запишите пожалуйста.

Если в первом примере событие «рождение мальчика» обозначить буквой A, то полученный результат записывают так: P(A) ≈ 0,512.

В жизни часто мы принимаем решения основываясь на вероятностных свойствах какого-то объекта или события. Например, товары популярных фирм стоят дороже аналогичных товаров малоизвестных фирм. Однако нередко мы покупаем более дорогой товар. Такое решение во многом определяется тем, что

вероятность купить некачественное изделие у известной фирмы меньше, чем у малоизвестной фирмы. Несмотря на это мы все же можем получить некачественный товар отдав предпочтение популярной фирме, или же товар окажется качественным, хотя куплен в малоизвестной фирме.

Но даже учитывая тот факт, что что отдельно взятый выбор, основанный на вероятностной оценке, может оказаться неудачным, отказываться от этого метода не стоит, поскольку такой подход увеличивает шансы на успех.

Слушают. Записывают.

Приводят свои примеры.

(Исход матча. Вызов к доске)

5. Отдых

Игра «День – ночь»:

Ребята делятся на 1 и 2 команду (в соответствии с номером варианта).

Звучит команда «ночь». Все ребята закрывают глаза и отдыхают.

Звучит команда «день». Ребята из команды 1 рассказывают соседу по парте определение случайного события.

Звучит команда «ночь». Все ребята закрывают глаза и отдыхают.

Звучит команда «день». Ребята из команды 2 рассказывают соседу по парте формулу нахождения частоты случайного события.

Для проверки работы учащихся можно спросить определение, которое он рассказывал, по одному ученику из каждой команды

Выполняют указания учителя.

6. Первичное закрепление

Устно решить номера 606, 607

Решить у доски номера

612.

Решение.

 Продолжительность рабочего дня 17-9=8 час.
Вероятность того, что телефон окажется свободным,
(8-6)/8 = 2/8 =0,25.

613.

Решение

Слушают учителя

Решают у доски

Теперь давайте проверим, как хорошо вы поняли тему, и ответим на вопросы теста.

(раздаются листочки с тестом - приложение 1)

Ученики отвечают на вопросы теста.

7. Постановка домашнего задания

Читать учебник стр. 159-163

Учить определения

Решить упражнения: №611, №614

Есть ли вопросы по домашнему заданию?

Записывают домашнее задание

Задают вопросы

8. Подведение итогов

Теперь давайте узнаем оценки за урок

(озвучиваются оценки)

Остались ли у вас вопросы по пройдённой теме?

Всем спасибо за урок. До свиданья!

Слушают оценки

Задают вопросы

1

2

3

4

5

0,1

0,3

0,8

0,5

0,1