Конспект урока по геометрии для учащихся 10 класса
Тема: «Признак перпендикулярности прямой и плоскости».
Цель урока:
Образовательная: расширить представления о перпендикулярности прямой и плоскости, закрепить вопросы теории по теме «Перпендикулярность прямой и плоскости»; выработать навыки решения основных типов задач на перпендикулярность прямой и плоскости.
Развивающая: развитие познавательных процессов учащихся, логического и математического мышления, воображения, устойчивости, гибкости и способности к распределению внимания.
Воспитательная: воспитание у учащихся аккуратности и точности при выполнении заданий у доски и ведения тетрадей, умения работать в коллективе, коммуникабельности, дисциплинированности на уроке, ответственности за свои действия, самостоятельности, воспитание интереса к предмету.
Тип урока: урок изучения нового материала
Методы обучения: индуктивно – репродуктивный.
Оборудование: набор чертежных инструментов.
Литература:
1.Геометрия, 10–11: учеб. для общеобразоват. учреждений: базовый и профил. Уровни/ [Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др.]. –16-е изд. – М.: Просвещение, 2007. –256 с.
2.Поурочные разработки по геометрии: 10 класс/ Сост. В.А. Яровенко.-М.: ВАКО, 2011.-304 с.- (В помощь школьному учителю).
3.Саранцев Г. И. «Упражнения в обучении математике»: Просвещение, 2005, с. 256
План урока:
Организационный момент(2 мин).
Актуализация знаний (5 мин).
Изучение нового материала (15 мин).
Закрепление изученного материала (20 мин).
Подведение итогов( 2 мин)
Домашнее задание (1 мин).
Ход урока:
Организационный момент
Включает в себя приветствие учителем учащихся, проверку отсутствующих, готовность помещения к уроку.
Деятельность учителя:
Запишите сегодняшнее число, классная работа и тему урока: «Признак перпендикулярности прямой и плоскости». Изучим теорему, выражающую признак перпендикулярности прямой и плоскости, выработаем навыки решения основных типов задач на перпендикулярность прямой и плоскости.
Запись на доске:
Число
Классная работа
Признак перпендикулярности прямой и плоскости
Актуализация знаний
| Деятельность учителя | Деятельность ученика |
| 1. Сформулируйте лемму о перпендикулярности двух прямых к третьей.
2. Какая прямая называется прямой перпендикулярной к плоскости
3.Сформулируйте теорему о связи между параллельностью прямых и их перпендикулярностью к плоскости
4.Сформулируйте теорему обратную теореме о связи между параллельностью прямых и их перпендикулярностью к плоскости | Если одна из двух параллельных прямых перпендикулярна к третьей, то и другая прямая перпендикулярна к этой прямой.
Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости.
Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна к этой плоскости
Если две прямые перпендикулярны к плоскости, то они параллельны. |
Изучение нового материала
Деятельность учителя
Мы с вами уже знаем, что прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости. Но в плоскости может находиться бесчисленное множество прямых и возникает сомнение, а существует ли такая прямая, которая перпендикулярна ко всем прямым, лежащим в этой плоскости. Признак, который мы с вами сегодня докажем, утверждает, что да, существует.
Итак, формулировка признака такова: Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна ко всем прямым, лежащим в этой плоскости.
Запись на доске и в тетрадях
Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна ко всем прямым, лежащим в этой плоскости.
Деятельность учителя
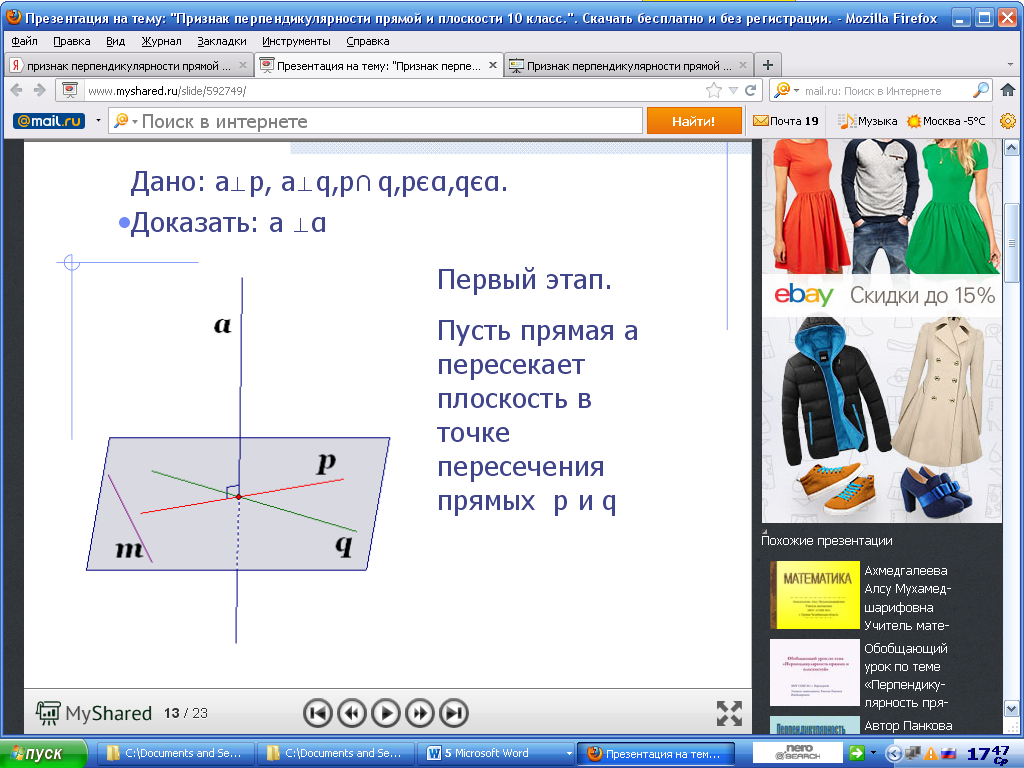
Дано: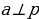 ;
; 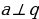 ;
;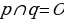 ;
; 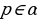 ;
;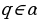
Доказать: 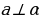 .
.
Доказательство:
При доказательстве мы будем использовать свойство серединного перпендикуляра к отрезку. Что называется серединным перпендикуляром к отрезку?
Деятельность ученика
Серединным перпендикуляром к отрезку называют, прямую, перпендикулярную к этому отрезку и проходящую через его середину.
Деятельность учителя
Нам нужно доказать, что 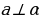 . Для этого нужно доказать, что прямая a перпендикулярна к любой (произвольной) прямой m на плоскости
. Для этого нужно доказать, что прямая a перпендикулярна к любой (произвольной) прямой m на плоскости 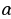 . Рассмотрим сначала случай, когда прямая a проходит через точку пересечения О.
. Рассмотрим сначала случай, когда прямая a проходит через точку пересечения О.
Запись на доске и в тетрадях
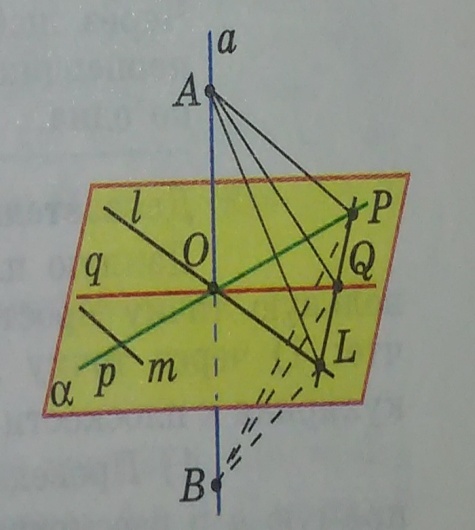
Деятельность учителя
Проведем через точку О прямую l, параллельную прямой m. Отметим на прямой a точки А и В, равноудаленные от точки O, и проведем в плоскости 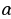 прямую, пересекающую прямые p, l и q соответственно в точках P, L и Q. Так как прямые p и q – серединные перпендикуляры, то АР=ВР и AQ=BQ. Следовательно, ∆APQ=∆BPQ (по трем сторонам). Тогда
прямую, пересекающую прямые p, l и q соответственно в точках P, L и Q. Так как прямые p и q – серединные перпендикуляры, то АР=ВР и AQ=BQ. Следовательно, ∆APQ=∆BPQ (по трем сторонам). Тогда 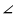 APL=
APL=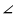 BPL и ∆ APL= ∆ BPL (по двум сторонам и углу). Тогда AL=BL. Следовательно, ∆ALB – равнобедренный, отрезок LO является медианой и высотой в этом треугольнике, то есть
BPL и ∆ APL= ∆ BPL (по двум сторонам и углу). Тогда AL=BL. Следовательно, ∆ALB – равнобедренный, отрезок LO является медианой и высотой в этом треугольнике, то есть 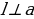 . Так как
. Так как 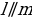 и
и 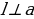 , то
, то 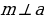 ( по лемме о перпендикулярности двух параллельных прямых к третьей). Итак, прямая a перпендикулярна к любой прямой m плоскости
( по лемме о перпендикулярности двух параллельных прямых к третьей). Итак, прямая a перпендикулярна к любой прямой m плоскости 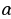 , то есть
, то есть 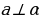 .
.
Запись на доске и в тетрадях
Проведем через точку О прямую l, параллельную прямой m. Отметим на прямой a точки А и В, равноудаленные от точки O, и проведем в плоскости 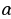 прямую, пересекающую прямые p, l и q соответственно в точках P, L и Q. Так как прямые p и q – серединные перпендикуляры, то АР=ВР и AQ=BQ. Следовательно, ∆APQ=∆BPQ (по трем сторонам). Тогда
прямую, пересекающую прямые p, l и q соответственно в точках P, L и Q. Так как прямые p и q – серединные перпендикуляры, то АР=ВР и AQ=BQ. Следовательно, ∆APQ=∆BPQ (по трем сторонам). Тогда 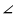 APL=
APL=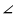 BPL и ∆ APL= ∆ BPL (по двум сторонам и углу). Тогда AL=BL. Следовательно, ∆ALB – равнобедренный, отрезок LO является медианой и высотой в этом треугольнике, то есть
BPL и ∆ APL= ∆ BPL (по двум сторонам и углу). Тогда AL=BL. Следовательно, ∆ALB – равнобедренный, отрезок LO является медианой и высотой в этом треугольнике, то есть 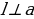 . Так как
. Так как 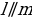 и
и 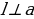 , то
, то 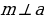 ( по лемме о перпендикулярности двух параллельных прямых к третьей). Итак, прямая a перпендикулярна к любой прямой m плоскости
( по лемме о перпендикулярности двух параллельных прямых к третьей). Итак, прямая a перпендикулярна к любой прямой m плоскости 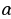 , то есть
, то есть 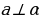 .
.
Закрепление изученного материала
Деятельность учителя
Давайте решим несколько задач на закрепление изученного материала. Прочитайте задачу под номером 121.
Деятельность ученика:
В Треугольнике АВС дано: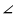 С=90
С=90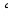 , АС=6 см, ВС=8см, СМ – медиана. Через вершину С проведена прямая СК, перпендикулярная к плоскости треугольника АВС, причем СК=12 см. Найдите КМ.
, АС=6 см, ВС=8см, СМ – медиана. Через вершину С проведена прямая СК, перпендикулярная к плоскости треугольника АВС, причем СК=12 см. Найдите КМ.
Деятельность учителя:
К доске пойдет …
К доске выходит ученик, остальные решают у себя в тетрадях.
| Деятельность учителя
| Деятельность ученика
| Запись на доске и в тетрадях |
| Какое важное условие нам дано, ориентируйтесь на то, какую тему мы сейчас изучаем?
Исходя из определения прямой перпендикулярной к плоскости, какой можем сделать вывод?
Тогда СК мы можем найти из какого треугольника?
| Прямая СК перпендикулярна к плоскости АВС.
Так как прямая перпендикулярная к плоскости АВС, значит, она перпендикулярна к любой прямой плоскости АВС.
Из прямоугольного треугольника КСМ.
| Дано: АВС-прямоугольный; 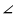 С=90 С=90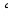 , АС=6 см, ВС=8см, СМ – медиана , АС=6 см, ВС=8см, СМ – медиана
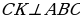 . СК=12 см . СК=12 см
Найдите КМ. 
Решение: 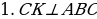 , отсюда следует, что , отсюда следует, что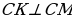 , значит ∆КСМ-прямоугольный. КМ-гипотенуза, найдем по т. Пифагора. , значит ∆КСМ-прямоугольный. КМ-гипотенуза, найдем по т. Пифагора.
КМ=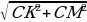 2.Найдем СМ. СМ=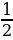 АВ АВ АВ=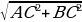 =10 =10 СМ=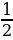 АВ=5. АВ=5. 3. КМ=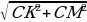 =13см =13см
Ответ: КМ=13 см |
Деятельность учителя:
Далее самостоятельно решите задачу 43из рабочих тетрадей под пунктами а и b.


Подведение итогов
Деятельность учителя:
Какую теорему мы доказали на сегодняшнем уроке?
Деятельность ученика:
Теорему, выражающую признак перпендикулярности прямой и плоскости
Деятельность учителя:
Сформулируйте данный признак
Деятельность ученика:
Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна ко всем прямым, лежащим в этой плоскости.
Повторяют теорему все ученики, с целью запоминания теоремы.
Деятельность учителя:
выставляет отметки за урок
Домашнее задание.
Деятельность учителя:
Упражнение 44 из рабочей тетради. № 120 из учебника.







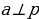 ;
; 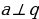 ;
;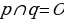 ;
; 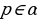 ;
;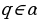
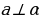 .
.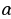 . Рассмотрим сначала случай, когда прямая a проходит через точку пересечения О.
. Рассмотрим сначала случай, когда прямая a проходит через точку пересечения О.
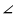 APL=
APL=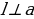 . Так как
. Так как 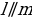 и
и 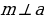 ( по лемме о перпендикулярности двух параллельных прямых к третьей). Итак, прямая a перпендикулярна к любой прямой m плоскости
( по лемме о перпендикулярности двух параллельных прямых к третьей). Итак, прямая a перпендикулярна к любой прямой m плоскости  , АС=6 см, ВС=8см, СМ – медиана. Через вершину С проведена прямая СК, перпендикулярная к плоскости треугольника АВС, причем СК=12 см. Найдите КМ.
, АС=6 см, ВС=8см, СМ – медиана. Через вершину С проведена прямая СК, перпендикулярная к плоскости треугольника АВС, причем СК=12 см. Найдите КМ.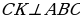 . СК=12 см
. СК=12 см
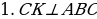 , отсюда следует, что
, отсюда следует, что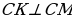 , значит ∆КСМ-прямоугольный. КМ-гипотенуза, найдем по т. Пифагора.
, значит ∆КСМ-прямоугольный. КМ-гипотенуза, найдем по т. Пифагора.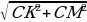
 АВ
АВ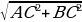 =10
=10











