Конспект урока "Наибольший общий делитель (НОД)"

Решим задачу. У нас есть  два типа печенья. Одни шоколадные, а другие простые. Шоколадных 48 штук, а простых 36. Необходимо составить из этого печенья максимально возможное число подарков, при этом надо использовать их все.

Для начала выпишем все делители каждого из этих двух чисел, так как оба эти числа должны делиться на количество подарков.

Получаем,  48: 1, 2, 3, 4, 6, 8, 12, 16, 24, 48.

36: 1, 2, 3, 4, 6, 9, 12, 18, 36.

Найдем среди делителей общие, которые есть как у первого, так и у второго числа.

Общими делителями будут: 1, 2, 3, 4, 6, 12.

Наибольшим из всех общих делителей является число 12. Это число называют наибольшим общим делителем чисел 36 и 48.

Исходя из полученного результата, можем заключить, что из всего печенья можно составить 12 подарков. В одном таком подарке будет 4 шоколадных печенья и 3 обычных печенья.

Определение наибольшего общего делителя

Наибольший общий делитель (НОД) двух данных чисел a и b - это наибольшее число, на которое оба числа a и b делятся без остатка.

Кратко наибольший общий делитель чисел a и b записывают так: НОД (a; b).

Пример: НОД (12; 36) = 12.

Некоторые пары чисел, например числа 24 и 35, имеют в качестве наибольшего общего делителя единицу. Такие числа называют взаимно простыми числами. 

Взаимно простые числа - это натуральные числа, которые имеют только один общий делитель - число 1. Их НОД равен 1.

Натуральное число, которое имеет более двух делителей называется составным.

Как найти наибольший общий делитель

Первый способ:

Найти НОД 48 и 36.

1. Разложить делители чисел на простые множители

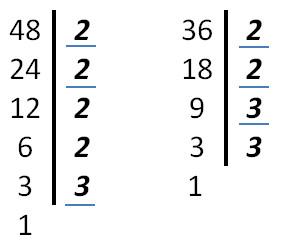
1. Подчёркиваем одинаковые простые множители в обоих числах. 

2. Находим произведение одинаковых простых множителей и записать ответ. 
   НОД (36; 48) = 2 • 2 = 4

 Второй способ:

Сначала разложить на простые множители оба числа.

48 = 2·2·2·2·3, 36 = 2·2·3·3.

Теперь из множителей, которые входят в разложение первого числа, вычеркнем все те, которые  не входят в разложение второго числа. В нашем случае это две двойки.

48 = 2·2·2·2·3, 36 = 2·2·3·3.

Останутся множители 2, 2 и 3. Их произведение равно 12. Это число и будет являться наибольшим общим делителем чисел 48 и 36. 

Эти правила можно распространить на случай с тремя, четырьмя и т.д. числами.

1. Разложить числа на простые множители.

2. Из множителей,  входящих в разложение одного из этих чисел, вычеркнуть те, которые не входят в разложение других чисел.

3. Посчитать произведение оставшихся множителей.

Наименьшее общее кратное (НОК)

Рассмотрим решение следующей задачи. Шаг мальчика составляет 75 см, а шаг девочки 60 см. Необходимо найти наименьшее расстояние, на котором они оба сделают по целому числу шагов.

Решение. Весь путь который пройдут ребята, должен делиться без остатка на 60 и на 70, так как они должны сделать каждый целое число шагов. Другими словами, в ответе должно быть число, кратное как 75 так и 60.

Сначала будем выписывать все кратные числа, для числа 75.

60, 120, 180, 240, 300, 360, 420, 480, 540, 600, 660, … .

Теперь находим числа которые есть в обоих рядах. Общими кратными чисел будут числа, 300, 600,  и т.д.

Самое наименьшее из них, это число 300. Оно в данном случае будет называться наименьшим общим кратным чисел 75 и 60.

Наименьшим общим кратным (НОК) двух и более натуральных чисел называется наименьшее натуральное число, которое само делится нацело на каждое из этих чисел.

Кратко наименьшее общее кратное чисел a и b записывают так: НОК (a; b).

Пример: НОК (6, 8) = 24

Возвращаясь к условию задачи, наименьшее расстояние, на котором ребята сделают целое число шагов будет 300 см. Мальчик пройдет этот путь за 4 шага, а девочке потребуется сделать 5 шагов.

Как найти наименьшее общее кратное

Первый способ:

Найти НОК 24 и 60.

1. Р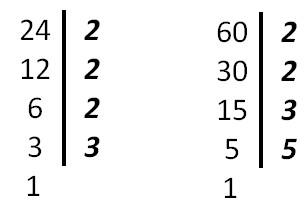азложить данные числа на простые множители

1. Выписать в строчку множители, входящие в разложение самого большого из чисел, а под ним - разложение остальных чисел.

Количество одинаковых множителей в разложениях чисел может быть разное.

60 = 2 • 2 • 3 • 5 24 = 2 • 2 • 2 • 3

1. Подчеркнуть в разложении меньшего числа (меньших чисел) множители, которые не вошли в разложение бóльшего числа (в нашем примере это 2) и добавить эти множители в разложение бóльшего числа. 

НОК (24, 60) = 2 • 2 • 3 • 5 • 2

1. Полученное произведение записать в ответ. 
   Ответ: НОК (24, 60) = 120

1. Если одно из чисел делится нацело на другие, то наименьшее общее кратное этих чисел равно этому числу.

Например, НОК (60, 15) = 60

1. Так как взаимно простые числа не имеют общих простых делителей, то их наименьшее общее кратное равно произведению этих чисел.

Пример. НОК (8, 9) = 72

1. Разложить числа на простые множители.

2. Выписать простые множители которые входят в состав одного из них.

1. Добавить к этим множителям все те, которые есть в разложении остальных, но нет в выбранном.

2. Найти произведение всех выписанных сомножителей.

Данный способ универсален. С его помощью можно найти наименьшее общее кратное любого количества натуральных чисел. 

Наибольший общий делитель

1. Пятиклассники решили сделать подарки первоклассникам. Они приготовили 69 шариков и 46 флажков и все их раздали малышам поровну. Сколько учеников в первом классе?

2. Два класса из 36 и 40 учеников. На праздники они построились в одну колонну с равным количеством школьников в каждом ряду. Как это можно сделать ?

3. Задача Бабы-Яги. Я в ступе в первый день привезла 35 кг топлива, во второй день 21 кг топлива для моей ступы, в 3 - й день14 кг. За каждый рейс я перевозила одинаковую массу топлива. Сколько килограмм я перевозила за один рейс.

4. а) Какое наибольшее число одинаковых подарков можно составить из 12 мандаринов и 16 бананов, если использовать все фрукты?

б) Во всех новогодних подарках всего было 185 мандаринов и 111 апельсинов. Сколько было подарков? Сколько мандаринов и сколько апельсинов было в каждом подарке?

1. а) Для новогодних подарков закупили 78 плиток шоколада, 156 пряников, 52 пачки печенья, 104 апельсина и 130 яблок. Какое наибольшее число одинаковых подарков можно собрать?

б) Для новогодних подарков купили 180 яблок, 90 апельсин и 900 конфет. Все дети получили одинаковые подарки. Какое наибольшее число одинаковых подарков было составлено из этих фруктов и конфет?

1. а) На новогодней елке все дети получили одинаковые подарки. Во всех подарках было 129 мандаринок и 86 шоколадок. Сколько ребят присутствовало на елке? Сколько мандаринок и сколько шоколадок было в каждом подарке?

б) Ребята получили на елке одинаковые подарки. Во всех подарках вместе было 123 апельсина и 82 яблока. Сколько ребят присутствовало на елке? Сколько апельсинов и сколько яблок было в каждом подарке?

1. а) Для подарков детям купили 80 штук апельсинов, 240 конфет и 320 орехов. Какое наибольшее количество одинаковых подарков можно изготовить и по сколько апельсинов, конфет и орехов будет в каждом подарке? .

б) Для приготовления подарков приобрели 200 пряников, 240 конфет и 320 орехов. Какое наибольшее количество одинаковых подарков можно приготовить для детей и сколько орехов, конфет и пряников будет положено в каждый пакет?

в)* Для устройства  елки  купили  орехов,  конфет и пряников - всего 760 штук. Орехов взяли на 80 штук больше, чем конфет, а пряников  на  120 штук меньше,  чем орехов. Какое наибольшее число одинаковых  подарков для детей можно сделать   из этого запаса?

1. а) Магазин получил елочные игрушки: 32 шарика, 48 колокольчиков и 56 звездочек. Сколько одинаковых комплектов можно составить из всех этих игрушек и по сколько игрушек каждого вида будет в комплекте?

б) Имеется 36 синих, 48 красных и 72 зеленых листа бумаги. Какое наибольшее число одинаковых комплектов цветной бумаги можно собрать из этих листов?

1. Для игры 24 ученикам дают 54 шара. На сколько групп надо поделить учеников, чтобы в каждой группе их было одно и то же наибольшее число, а также одинаковое число шаров?

2. Сколько букетов можно сделать из 18 желтых и 24 красных роз, если в каждом букете должно быть наибольшее, но во всех букетах одинаковое количество желтых и одинаковое количество красных роз?

3. а) Из 210 бордовых, 126 белых, 294 красных роз собрали букеты причем в каждом букете количество роз одного цвета поровну. Какое наибольшее количество букетов сделали из этих роз и сколько роз каждого цвета в одном букете?

б) Из 156 чайных, 234 белых и 390 красных роз сделали букеты. Причем во всех букетах роз каждого вида было поровну и число таких букетов было больше 50. Сколько букетов сделали из этих роз и сколько роз каждого вида было в одном букете?».

1. Для участи в эстафете нужно разделить 36 девочек и 24 мальчика на команды с одинаковым числом участников, состоящих только из девочек или только из мальчиков. Какое наибольшее число человек может быть в каждой команде? Сколько команд получится?

2. На соревнованиях по настольному теннису участвовали равные по количественному команды, в которых всего 145 мальчиков и 87 девочек. Во всех командах было одинаковое число мальчиков и одинаковое число девочек. Сколько команд участвовало в соревнованиях? Сколько девочек и сколько мальчиков было в каждой команде?

3. Из школы в день здоровья 424 человека повезли на стадион, а 477 – в плавательный бассейн. Для этого заказали несколько автобусов с одинаковым числом мест в каждом. Все места в автобусе были заняты, и никто не стоял. Сколько автобусов было заказано и сколько пассажиров было в каждом автобусе?

4. Для первоклассников купили 270 фломастеров и 675 карандашей. Какое наибольшее число подарков можно приготовить, чтобы в них было одинаковое число фломастеров и одинаковое число карандашей? Сколько фломастеров и карандашей будет в каждом подарке?

5. Садовый участок размером 54 м × 48 м по периметру необходимо оградить забором, для этого через равные промежутки надо поставить бетонные столбы. Сколько столбов необходимо привезти для участка, и на каком максимальном расстоянии друг от друга будут стоять столбы?

6. Если мы хотим сделать ремонт в комнате - надо знать ее длину и ширину. Например, длина нашей комнаты 575 см, а ширина 375 см. Пол в комнате нужно выложить декоративными плитками в форме квадрата. Каков наибольший возможный размер такого квадрата? Сколько плиток такого размера, понадобится?

7. * а) Лист картона имеет форму прямоугольника, длина которого 48 см, а ширина 40 см. Этот лист надо разрезать без отходов на равные квадраты. Какие наибольшие квадраты можно получить из этого листа и сколько?

б) Лист картона имеет форму прямоугольника. Его длина равна 24 см, ширина - 16 см. Какие наибольшие равные квадраты можно получить из этого листа, если его разрезать без отходов?

в) Лист картона со сторонами 54см и 36 см надо разрезать без отходов на равные квадраты. Найдите площадь наибольшего квадрата, который можно получить из этого листа.

1. Камин в комнате необходимо выложить отделочной плиткой в форме квадрата. Сколько плиток понадобится для камина размером 195 × 156 см и каковы наибольшие размеры плитки?

2. Ася и Вася играли со спичками, составляя из них различные правильные многоугольники. У Аси было 12 спичек, а у Васи – 18. Сколько они смогут составить одинаковых многоугольников с наибольшим числом сторон так, чтобы были использованы все спички?

3. В класс привезли учебники: по математике 24, по истории 36 и по географии 48. Какое наибольшее число комплектов можно составить из этих книг так, чтобы в каждом было одинаковое число книг по математике, истории и географии? По сколько книг будет в каждом комплекте?

4. а) Миша и Саша покупают одинаковые почтовые наборы. Каждый набор состоит из открытки с конвертом, и его цена выражается целым числом рублей. Миша заплатил за наборы 85 рублей, а Саша – на 34 рубля больше. Сколько стоит 1 набор? Сколько наборов купил Миша? Сколько наборов купил Саша?

б) Таня и Маша купили одинаковое число почтовых наборов. Таня заплатила 90 руб., а Маша на 5 руб. больше. Сколько стоит 1 набор? Сколько наборов купила каждая?

в) Я и моя подруга Юля решили купить одинаковые наборы. Каждый набор состоит из открытки с конвертом. Я заплатила за наборы 65 руб., а Юля - на 26 руб. больше. Сколько стоит один набор? Сколько наборов купила Я? А Юля?

1. На соревнованиях по бегу через каждые 300 м от старта стоит наблюдатель, а через каждые 800 м от старта можно попить воды. На каком минимальном расстоянии от старта можно попить воды рядом с наблюдателем?

2. Туристы проехали за 1 день 56 км, а за 2 – 72 км, причем их скорость была одинаковой и выражалась целым числом км/ч, и каждый день они были в пути целое число часов. Найдите скорость, с которой ехали туристы, если она была наибольшей из удовлетворяющих условию задачи. 

3. Найти НОД делимого и делителя в частном: а) 720 : 144; б) 6812 :1703.

4. НОД (m, n) = НОД (m-n, n). Пользуясь свойством делимости разности, найти НОД:

а) 70 И 42; в) 579 и 592; д)482 и 4484;

б) 100 и 85; г) 378 и 270; е) 1001 и 998.

1. Найти НОД (m, n,c), если n - делитель m; n и c – взаимно простые числа. Привести пример.

2. Разность двух чисел является делителем каждого из этих чисел и равна 60. Чему равен их наибольший общий делитель.

Наименьшее общее кратное

1. а) Шаг Володи 75 см, а шаг Кати 60 см. На каком наименьшем расстоянии они оба сделают по целому числу шагов?

б) Шаг папы 90 см, а шаг мамы 80 см. На каком наименьшем расстоянии от начала движения они оба сделают по целому числу шагов?

1. Одно колесо, сделав полный оборот, проходит путь 105 см, другое 165 см. Найдите наименьшее расстояние, на котором оба колеса сделают по целому числу оборотов?

2. Диаметр заднего колеса гиганта-грузовика – 3 м, а переднего – 2 м. Найти наименьшее расстояние, которое пройдет грузовик, чтобы каждое колесо сделало целое число оборотов.

3. Никита пригласил к себе на день рождения трёх своих друзей и приготовил для них сладкое угощение – миндальный торт. Однако он не знает, сколько из них смогут откликнуться на его приглашение. На сколько равных кусков ему следует разрезать торт, чтобы всем участникам застолья досталось поровну?

4. По плану парада физкультурники сначала должны маршировать строем по 12 человек в шеренге. Потом они должны перестроиться в колонну по 18 человек в шеренге. Сколько физкультурников можно пригласить для участия в параде?

5. Если участники демонстрации построятся по 10 человек в ряд, то 1 человек останется лишним. Если они построятся 9 человек в ряд, то опять один человек останется лишним. То же самое произойдет, если они построятся по 8;7;6;5;4;3 и наконец, по 2 человека в ряд. Всего их меньше 5 тысяч человек. Сколько их?

6. Отец и сын решили перемерить шагами расстояние между двумя     деревьями, для чего отошли одновременно от одного и того же дерева. Длина шага отца - 70см, сына - 56 см. Найти расстояние между этими деревьями,  если известно,  что следы их  совпали 10 раз.

7. а) В депо из одинаковых вагонов было сформировано 2 поезда. Первый – на 456 пассажиров, второй – на 494 пассажира. Сколько вагонов в каждом поезде, если известно, что общее число вагонов не превышает 30?

б) На станции стоят 3 пассажирских поезда: в первом – 418 мест в купейных вагонах, во втором – 494, а в третьем – 456. Сколько купейных вагонов в каждом поезде, если в каждом вагоне одинаковое число мест и их число больше 20?

1. На экскурсию по рекам и каналам отправились несколько катеров, где было одинаковое количество мест. В 12 ч отправились 387 человек, а в 13 ч – 430 человек. Все места на катерах были заняты. Сколько катеров отправилось на экскурсию и сколько мест было на каждом катере?

2. Первую половину пути Ефим ехал со скоростью16 км/ч, а вторую половину пути со скоростью – 24 км/ч, а Фома ехал весь путь со скоростью 20 км/ч. Какой путь они проехали? Кто быстрее приехал?

3. Найдите ошибку! Ученица нашла НОК(33, 198) и получила 99. Не проверяя вычислений, учитель определил, что была допущена ошибка. Как это он сделал?

4. Какой наименьшей длины ленту должна купить Мальвина, чтобы разрезать ее на ленты по 35 см или по 50 см, не получив обрезков?

5. Какой наименьшей длины должна быть доска, чтобы ее можно было разрезать поперек на части, равные 20 см или 27 см, не получая обрезков?

6. Какой наименьшей длины должна быть веревка, чтобы ее можно было разрезать на равные части по 25 см или по 35 см, не получая обрезков?

7. Какой наименьшей длины должны быть ящики, чтобы в них можно было вкладывать изделия длиной по 12 см и по 8 см без свободного места?

8. Какой наименьшей длины нужно сделать заготовку, чтобы ее можно было разрезать на куски длиной по 24 см и по 36 см без потери материала?

9. У Васи в коллекции есть 380 марок с изображением цветов, а также 399 марок с изображением животных и насекомых. Он купил для них два альбома, все страницы которых вмещают одинаковое количество марок. Сколько марок вмещает каждая страница этих альбомов, если на любой из них помещается более 16 марок? 

10. Миша бывает в радиотехническом кружке каждый шестой день, Вова – каждый четвертый, Олег – каждый пятый. Сегодня они были в кружке. Через сколько дней Миша, Вова и Олег встретятся на занятии?

11. Коля, Серёжа и Ваня регулярно ходили в кинотеатр. Коля бывал в нём каждый 3-й день, Серёжа  — каждый 7-й, Ваня  — каждый 5-й. Сегодня все ребята были в кино. Когда все трое встретятся в кинотеатре в следующий раз? На 105 день

12. Саша ходит в бассейн один раз в три дня, а Вася один раз в четыре дня, Ваня – в 5 дней. Они встретились в бассейне в этот понедельник. Через сколько дней и в какой день недели они встретятся снова?

13. Три ученика договорились пропускать занятия в разные дни, чтобы учитель не заметил. Первый стал пропускать каждый 4-й день занятий, второй – каждый 3-й день, третий – каждый 6-й день. Один из них сказал, что наступит день, когда всех троих не будет в школе. Прав ли он? Если да, то когда наступит этот день? Можно ли выбрать дни пропусков так, чтобы такого не произошло в течение первых 80 дней занятий?

14. а) Оля ходит в бассейн раз в 4 дня, Маша – в 6 дней, Ваня – в 8 дней. Они все были в бассейне 4 октября. Через сколько дней Оля, Маша и Ваня встретятся снова?

б) В бассейне встретились Валера, Марк и Антон. Через какое наименьшее время повторится их встреча, если они ходят в бассейн строго по расписанию: Валера – через 5 дней, Марк – через 12, Антон – через 10?

1. Наташа ходит на каток раз в 2 дня, Аня – в 3 дня, Люда – в 4 дня. Они все встретились на катке в воскресенье. Через сколько дней подруги снова соберутся вместе?

2. Сегодня в командировки отправятся 3 сотрудника: первый – на 15 дней, второй – на 20 дней, третий – на 12 дней. Через сколько дней они все снова увидятся?

3. Из речного порта одновременно 1 мая 2013 года вышли два теплохода. Продолжительность рейса одного из них – 15 суток, а продолжительность второго – 24 суток. Через сколько дней теплоходы снова одновременно отправятся в рейс? Сколько рейсов за это время сделает первый теплоход? А сколько второй?

4. Теплоход «Суворов» свой рейс туда и обратно совершает за 8 дней, теплоход «Горький» за 12 дней, а теплоход «Киров» за 18 дней. Через сколько дней теплоходы снова встретятся в порту, если они ушли в рейс одновременно?

5. От станции одновременно отправляются 2 поезда. У одного рейс туда и обратно длится 48 ч, у другого - 72 ч. Через какое время поезда снова встретятся на этой станции?

6. Теплоход первой линии совершает свои рейсы, возвращаясь и отправляясь в плавание каждые 12 дней, а теплоход второй линии – каждые 28 дней. Через какое наименьшее время произойдет их встреча в пункте отправления, если они отправляются в рейс одновременно?

7. В портовом городе начинаются три туристских теплоходных рейса, первый из которых длится 15 суток, второй – 20 и третий – 12 суток. Вернувшись в порт, теплоходы в этот же день снова отправляются в рейс. Сегодня из порта вышли теплоходы по всем трем маршрутам. Через сколько суток они впервые снова вместе уйдут в плавание? Какое количество рейсов сделает каждый теплоход?

8. У моей московской подруги Оли родители работают водителями трамваев: мама на маршруте «А», папа на «Б». Один рейс маршрута «А» длится 48 мин, а маршрута «Б» 72 мин. У этих маршрутов есть общая конечная станция, и вскоре после начала работы вагоны подошли к ней одновременно. Через какое время Олины родители снова встретятся на этой станции?

9. Муж получает на работе премию 1 раз каждые 8 месяцев, а жена – 1 раз в полгода. В этом году они получили премии одновременно под Новый год. Через какое наименьшее время они получат премии одновременно?

10. а) Два автобуса одновременно отправляются от одной площади по разным маршрутам. У одного рейс туда и обратно длится 48 минут, а у другого 1 час 12 минут. Через сколько времени автобусы снова встретятся на этой площади?

б) Два троллейбуса разных маршрутов встречаются на одной общей остановке. У одного троллейбуса весь рейс длится 50 минут, у другого – 1 час 30 мин.. Через сколько времени троллейбусы вновь встретятся на этой остановке?

1. По трем различным маршрутам из Перми курсируют три автобуса. Продолжительность маршрута первого автобуса – 8 ч, второго – 6 ч и третьего – 4 ч. Через сколько часов после одновременного выезда из Перми все три автобуса снова встретятся в Перми? Нок

2. Три автобуса в 6 ч утра отправились с одной и той же станции по трем разным маршрутам и совершают рейс туда и обратно; первый автобус – за 40 минут, второй – за 1 ч и третий – за 50 мин. Через какое наименьшее время все три автобуса одновременно отправятся с той же станции?

3. На остановке одновременно встретились трамвай, троллейбус и автобус. Через какое наименьшее время в этом месте повторится их встреча, если движение по круговому маршруту проходит строго по графику, при этом трамвай совершает рейс за 90 мин., автобус – за 120 мин., троллейбус – за 60 мин.?

4. Три велосипедиста стартуют из одной точки и движутся по круговому велотреку. Первый проезжает круг за 40 секунд, второй за 50 секунд, а третий за 45 секунд. Через какое время они снова окажутся вместе на точке старта?  

5. Аня и Ваня катались в парке атракционов на двух расположенных рядом каруселях. Первая карусель делает полный оборот за 12 секунд, а вторая – за 18. Через какое время Аня и Влад снова окажутся на кратчайшем расстоянии друг от друга, если перед пуском каруселей они сели на ближайшие места?

6. а) Конфеты «Сладкая математика» продаются по 12 штук в коробке, а конфеты «Геометрия с орехами» – по 15 штук в коробке. Какое наименьшее число коробок конфет того и другого сорта необходимо купить, чтобы тех и других конфет было поровну?

б) К празднику решили купить конфеты «Белочка» (они продаются по 30 штук в коробке) и конфеты «Снегурочка» (по 20 штук в коробке). Но нужно, чтобы тех и других конфет было поровну. Какое наименьшее число коробок «Белочки» и «Снегурочки» необходимо купить?

1. Вдоль дороги от пункта К стоят столбы электролинии через каждые 45 м. Эти столбы решили заменить другими, поставив их на расстоянии 60 м друг от друга. Сколько столбов было и сколько будут стоять?

2. Вдоль аллеи через каждые 15 м посадили кусты шиповника, а через каждые 18 м - березы. Через сколько метров от начала аллеи куст шиповника окажется рядом с березой?

3. а) На столе лежат книги, число которых меньше, чем 100. Сколько лежит книг, если известно, что их можно связывать пачки по 3, по 4, и по 5 штук?

б) На полках лежат книги, число которых меньше, чем 100. Сколько всего книг, если известно, что их можно расставить на полках по 3, по 4, по 5 штук, по 6 штук?

1. Маленькая коробочка вмещает шесть яиц, а большая – десять яиц. Найдите наименьшее число яиц, которое может быть разложено как в маленькие коробки, так и в большие?

2. Мальчик расскладывал орехи. Когда он их раскладывал по 2, по 3, по 4, по 5 и по 6, то каждый раз оставался один орех. Сколько было орехов у мальчика, если известно, что их было менее 100?

3. На складе  имеются ножи и вилки. Общее число тех и других больше  300, но меньше 400.  Если ножи и вилки вместе считать десятками или дюжинами, то в обоих случаях  получается  целое число десятков и целое  число  дюжин. Сколько  было  ножей и  вилок на складе,  если ножей было на 160 меньше, чем вилок?  

4. В детском велосипеде шестерня заднего колеса имеет 21 зубец, а шестерня педали 44 зубца. Какое наименьшее число оборотов должна сделать педаль, чтобы шестерни вернулись в свое первоначальное положение?

5. Малая шестерня имеет 6, а большая – 18 зубцов. Какое наименьшее количество оборотов должна сделать педаль, чтобы заднее колесо велосипеда и большая шестерня возвратились в первоначальное положение?

6. Два зубчатых колеса, радиусы которых 20 см и 8 см, сцеплены друг с другом. Большое колесо вращается со скоростью 10 оборотов в секунду. Сколько оборотов в секунду будет при этом делать меньшее колесо?

7. Убедитесь, что НОД(36, 24) ∙ НОК(36, 24) = 36 ∙ 24

8. Проверьте равенство НОК(х, у) ∙ НОД(х, у) = х ∙ у, если х = 28, у = 21

9. а) На какое наименьшее число нужно умножить 35, чтобы полученное произведение было кратно 3, 5 и 2.

б) На какое наименьшее число нужно умножить 144, чтобы полученное произведение было кратно 4, 5 и 9.

в) На какое наименьшее число нужно умножить 121, чтобы полученное произведение было кратно 2, 3 и 121.

1. Маша для Медведя купила в магазине яйца. По дороге в лес она сообразила, что число яиц делится на 2, 3, 5, 10 и 15. Сколько яиц купила Маша?

2. а) Школьники построились в ряды по 6 человек в каждом. Затем их перестроили по 4 человека в ряд. Сколько было школьников, если известно, что их было больше 70, но меньше 80?

б) Учеников одного класса построили для похода в ряды по 6 человек, а потом перестроили по 4 человека в ряд. Сколько учеников в классе, если их меньше 50, но больше 40?

1. Сколько солдат маршируют на плацу, если они будут маршировать строем по 12 человек в шеренге и перестраиваться в колонну по 18 человек в шеренге?

2. Солдаты выстроились в ряды, по 12 человек в каждом, а затем перестроились по 8 человек в ряду. Сколько было солдат, если больше 180, но меньше 200?

3. На базар привезли арбузы. Если их считать десятками, то получится целое число десяток. Если считать дюжинами (по 12), то опять получится целое дюжин. Сколько арбузов привезли на базар, если их больше 300, но меньше 400?

4. Конструкторское бюро получило 74 справочника и 111 наборов карандашей, которые поровну разделили между работниками. Сколько работников в конструкторском бюро, если известно, что их больше 35?

5. * Требуется изготовить ящик с квадратным дном для укладки коробок размером 16×20 см. Какова должна быть наименьшая длина стороны квадратного дна, чтобы уместить коробки в ящик вплотную?

6. Тетрадь стоит 15 коп. У покупателя 10 монет по 20 коп., а у продавца нет сдачи. Какое наибольшее количество тетрадей может купить покупатель?

7. Сергей хочет купить несколько пачек мороженного по 39 р., но у него только 5-рублевые монеты, а у продавца нет сдачи. Какое наименьшее число пачек мороженного он может купить?

8. Из двух натуральных чисел одно в 3 раза больше другого. Сравнить наименьшее общее кратное и наибольший общий делитель этих чисел.

9. Представить число 100 в виде суммы таких двух слагаемых, чтобы их НОК было в 9 раз больше их НОД. (Попробуйте использовать свойство: если одно число кратно другому, то большое из них является НОК, а меньшее – НОД этих чисел).

10. Найти НОД двух натуральных чисел, НОК которых равно их произведению. Привести обоснование способа решения.

11. ** В магазин привезли меньше 600, но больше 500 тарелок. Когда стали раскладывать их десятками, то не хватило 3 тарелок до полного числа десятков, а когда стали раскладывать дюжинами (по 12 тарелок), то осталось 7 тарелок. Сколько тарелок привезли в магазин ?

Задания для самостоятельной работы

1. НОД(720,216) равен

а) 36; б) 72; в) 18; г) 54; д) 108; е) другой ответ

1. НОК(720,216) равен

а) 2880; б) 4320; в) 2160; г) 1440;

д) 3600; е) другой ответ

1. Обвести верные утверждения:

а) НОК(70,280)=440; б) НОК(135,28)=536;

в) НОК(72,45)=360; г) НОК(27,32)=1368;

д) НОД(70, 280)=140; е) все утверждения неверны

1. Вычислить НОК(18,24,28).

а) 12096; б) 1008; в) 504; г) 126;

д) 432; е) другой ответ

1. Найти НОК(84,140,40).

а) 4; б) 420; в) 840; г) 3360; д) другой ответ

1. Найти НОК(84,160,96).

а) 4; б) 1120; в) 3360; г) 13640; д) другой ответ

1. Найти наибольший общий делитель и наименьшее общее кратное чисел 22 ∙ 3 ∙ 7 и 2 ∙ 32 ∙ 72.

2. Найти частное от деления НОК(154, 220) на НОД тех же чисел.

а) 10; б) 22; в) 70; г) 110;

д) 1540; е) другой ответ

1. Найти частное от деления НОК(24, 2004) на НОД тех же чисел.

а) 12; б) 34; в) 100; г) 334;

д) 4008; е) другой ответ

1. Найти частное от деления НОК(95,3610) на НОД тех же чисел.

а) 95; 6) 361; в) 1805;

г) 19; д) 475; е) другой ответ

1. Отношение НОК (308,264) к НОД (308,264) равно:

а) 21; 6)616; в) 42; г) 66;

д) 3; е) другой ответ

1. Отношение НОК(975, 819) к НОД этих же чисел равно

а) 525; б) 39; в) 20475; г) 552;

д) 38025; е) другой ответ

1. Найти: а) НОД(1512,1260,105) = ______.

б) НОД(11088;5292) =______;

1. Найти: НОК(360;252)=_______.

2. Найти х, если известно, что: НОД (2х, 12)=2,

НОК(Зх, 2)=30. х = ________

1. НОД (а; b)=5; НОК(а; b)=165. Найти хотя бы одну пару чисел а и b. Ответ: _____

2. * Найти а и b, если число 570a8b кратно 45. Ответ: а=___; b=____

3. Будет ли число а кратно b, если а =25341119; b =243419? Разделить число а на b.

а) будет; б) не будет.

Результат деления:____________

1. Выписать все общие делители чисел 444, 555, 666.

2. * Найти: а) НОК(308,264); б) Найти НОК(1998, 8991).

3. Числа 1136 и 513 делили на одно и то же наибольшее натуральное число, при этом получили остатки 11 и 13 соответственно. На какое число делили?

4. * Коля Пузатов раньше съедал булочек на 60 рублей в день. Когда у него совсем не оставалось денег, он шел к любимой мамуле и получал определенную сумму авансом на булочки. Потом Коля Пузатов подрос и стал съедать булочек на 75 рублей в день. Получив ту же сумму от мамы он обнаружил, что сдачи у него опять совсем не остается. Какую наименьшую сумму давала ему мама на булочки авансом?  

5. К новому году Коля Пузатов купил в городе 48 хомяков и 36 кофейников. Фекла Дормидонтова, как самая честная девочка класса, получила задание разделить это имущество на наибольшее возможное число подарочных наборов для учителей. Какое число наборов получилось?

6. Мальчик хочет купить несколько порций мороженого по 33 пенса каждое, у него есть только монеты по 15 пенсов, а у продавца нет сдачи. Каково наименьшее число порций мороженого, которое сможет купить мальчик?

7. Три велосипедиста стартуют из одной точки и движутся по круговому велотреку. Первый проезжает круг за 40 секунд, второй за 50 секунд, а третий за 45 секунд. Через какое время они снова окажутся вместе на точке старта? 

8. У Васи в коллекции есть 380 марок с изображением цветов, а также 399 марок с изображением животных и насекомых. Он купил для них два альбома, все страницы которых вмещают одинаковое количество марок. Сколько марок вмещает каждая страница этих альбомов, если на любой из них помещается более 16 марок? 

9. Найдите все пары натуральных чисел, наименьшее общее кратное которых равно 78, а наибольший общий делитель равен 13.

10. Найдите все пары натуральных чисел, разность которых 66, а наименьшее общее кратное равно 360.

11. Натуральные числа a,b и с таковы, что НОК(a,b) = 60, НОК(a,c) = 270 (НОК(x,y) - наименьшее общее кратное чисел х и у). Найдите НОК(b,с).

12. * Каким может быть наибольший общий делитель натуральных чисел m и n, если при увеличении числа m на 6 он увеличивается в четыре раза?

13. Если натуральное число делится на а и на в, то оно делится и на произведение ав. Каким свойством должны обладать натуральные числа а и в, чтобы это утверждение было верным? Для каких натуральных чисел а и в это утверждение неверно?

14. Определите, может ли сумма двух взаимно простых чисел иметь с одним из этих чисел наибольший общий делитель, больший единицы.

15. * Найдите наименьшее натуральное число, которое кратно 2, 3, 4, 5, 6, 7, 8, 9, 10.

16. Если из некоторого трехзначного числа вычесть 7, то полученная разность будет делиться на 7, если вычесть 8, то разность будет делиться на 8, если вычесть 9, то разность будет делиться на 9. Найдите наименьшее такое число.

17. а) НОД(а, в) = а. Найдите НОК(а, в).

б) НОК(а, в) = в. Найдите НОД(а, в).

1. * Наименьшее общее кратное двух чисел равно 120. Найдите эти числа, если частные от их деления на их наибольший общий делитель соответственно равны 4 и 5.

2. Даны числа а, в и с, причем а делится на в и в делится на с. Найдите НОД(а, в, с) и НОК(а, в, с).

3. Витя раскладывал орехи кучками. Если он раскладывает в кучки по 3, 5 и 7 штук, то получается натуральное число полных кучек. Какое минимальное число орехов может быть у Вити?

Ответы

29