Класс: 9 Урок №__ Четверть: 2 Дата: _________
Тема: степенная функция с натуральным показателем и её график.
Цели:
-Изучить свойства и график степенной функции; формировать умение строить и различать графики степенных функций с четными и нечетными показателями.
-Расширять пространственные представления и аналитические способности мышления.
- Воспитывать внимательность и уверенность при работе у доски и в тетради.
Оборудование: учебник, презентация с чертежами и таблицей для устной работы и объяснения новой темы; текст самостоятельной работы на карточках.
Ход урока
I. Организационный момент.
II. Проверка д/з: № 131,132 (фронтально).
III. Устная работа.
По графику функции у = ах2 + bх + с определите знаки коэффициентов а, b и с:
а)  б)
б) 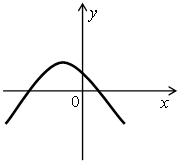
IV. Объяснение нового материала.
Учитель создает условия для самостоятельной работы учащихся, предложив им сделать основные выводы и перечислить свойства новой функции.
1. Предложить учащимся построить в одной системе координат графики функций у = х2, у = х4 и у = х6, заполнив таблицы значений этих функций.
| х | –2 | –1,5 | –1 | –0,5 | 0 | 0,5 | 1 | 1,5 | 2 |
| у |
|
|
|
|
|
|
|
|
|
В о п р о с ы:
– В чем состоит сходство построенных графиков?
– Чем отличаются графики функций?
– Как будут выглядеть графики функций у = х8 и у = х10?
– Может ли функция у = х18 принимать отрицательные значения?
2. Построить в одной системе координат графики функций у = х3 и у = х5.
Во п р о с ы:
– В чем состоит сходство построенных графиков?
– Чем отличаются графики функций?
– Как будет выглядеть график функции у = х7?
– Может ли функция у = х9 принимать отрицательные значения?
3. -Функции, графики которых строили, называются степенными функциями с натуральным показателем и записываются в общем виде:
Чтение определения в учебнике, запись определения в тетрадь.
В о п р о с : на какие две группы можно разбить все степенные функции? Перечислите свойства каждой из выделенных групп.
| у = х2п | у = х2п + 1 |
| 1) D (у) = R; 2) Е (у): [0; +∞); 3) у = 0 при х = 0; 4) если х ≠ 0, то у 0; 5)  : [0; +∞), : [0; +∞),  : (–∞; 0]. : (–∞; 0]. 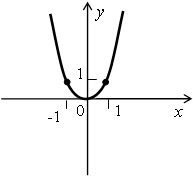 | 1) D (у) = R; 2) Е (у) = R; 3) у = 0 при х = 0; 4) у 0, если х  (0; +∞), (0; +∞), у х  (–∞; 0); (–∞; 0); 5) Функция возрастающая. 
|
V. Формирование умений и навыков.
1. Определите, график какой функции изображен на рисунке?
| а) 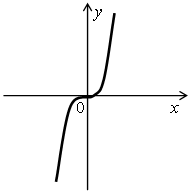 | у = х16 у = –2х10 у = х11 у = х2 + 2х |
| б)  | у = х2 – 4х у = х3 у = х9 у = х12 |
2. № 142.
3. № 146.
4. № 136, № 137.
5-6. Самостоятельно (первичный контроль знаний и умений):
5. Функция задана формулой f (х) = х32. Сравните:
а) f (1,7) и f (4); в) f (–5) и f  ;
;
б) f (–2,1) и f  ; г) f (20) и f (–17).
; г) f (20) и f (–17).
6. Функция задана формулой g (х) = х37. Сравните:
а) f (3,6) и f (4,7); в) f (50) и f (–40);
б) f  и f (–2); г) f (25) и f (–25).
и f (–2); г) f (25) и f (–25).
7. Проверка выполнения с/р. Коррекция знаний.
VI. Итог урока.
В о п р о с ы у ч а щ и м с я:
– Какая функция называется степенной функцией с натуральным показателем?
– На какие две группы можно разделить степенные функции?
– Перечислите свойства степенной функции с четным показателем.
– Перечислите свойства степенной функции с нечетным показателем.
Общая оценка работы на уроке. Сообщение индивидуальных отметок.
VII. Домашнее задание: 139,141
| Самостоятельная работа 1.Функция задана формулой f (х) = х32. Сравните: а) f (1,7) и f (4); в) f (–5) и f  ; ; б) f (–2,1) и f  ; г) f (20) и f (–17). ; г) f (20) и f (–17).
2. Функция задана формулой g (х) = х37. Сравните: а) f (3,6) и f (4,7); в) f (50) и f (–40); б) f  и f (–2); г) f (25) и f (–25). и f (–2); г) f (25) и f (–25).
|







 б)
б) 














