Р
АЗДЕЛ 2. ИНФОРМАЦИЯ И ИНФОРМАЦИОННЫЕ ПРОЦЕССЫ
Тема 2.3. Представление информации в системах счисления
2.3.1. Общие положения о системах счисления Для обмена информацией с другими людьми человек использует естественные языки. В основе языка лежит алфавит - набор символов (знаков), которые человек различает по их начертанию. В основе русского языка лежит кириллица, содержащая 33 знака, английский язык использует латиницу (26 знаков), китайский язык использует алфавит из десятков тысяч знаков (иероглифов).
Последовательности символов алфавита, в соответствии с правилами грамматики, образуют основные объекты языка - слова. Правила, согласно которым образуются предложения из слов данного языка, называются синтаксисом.
Формальные языки имеют жестко зафиксированный алфавит и строгие правила (без исключений) грамматики и синтаксиса.
Представление информации может осуществляться с помощью языков, которые являются знаковыми системами. Каждая знаковая система строится на основе определенного алфавита и правил выполнения операций над знаками.
Система счисления (СС) - это знаковая система, в которой числа записываются по определенным правилам с помощью символов некоторого алфавита, называемых цифрами.
Все системы счисления делятся на две группы: позиционные и непозиционные. В позиционных системах счисления значение цифры зависит от ее положения в числе, а в непозиционных - не зависит. Самой распространенной из непозиционных систем счисления является римская. В качестве цифр в римской системе используются: I(1), V(5), X(10), L(50), С(100), D(500), М(1000). Значение цифры не зависит от ее положения в числе.
Пример, в числе XXX(30) цифра X встречается трижды и, в каждом случае, обозначает одну и ту же величину - число 10, три раза по 10 в сумме дают 30.
Величина числа в римской системе счисления определяется как сумма или разность цифр в числе. Если меньшая цифра стоит слева от большей, то она вычитается, если справа - прибавляется.
Например, запись десятичного числа 1998 в римской системе счисления будет выглядеть следующим образом: MCMXCVIII = 1000 + (1000 - 100) + (100 - 10) + 5 + 1 + 1 + 1.
Первая позиционная система счисления была придумана еще в древнем Вавилоне, причем вавилонская нумерация была шестидесятеричной. До сих пор при измерении времени мы используем основание, равное 60 (в 1 минуте содержится 60 секунд, а в 1 часе - 60 минут).
В девятнадцатом веке довольно широкое распространение получила двенадцатеричная система счисления. До сих пор мы часто употребляем дюжину (число 12): в сутках две дюжины часов, круг содержит тридцать дюжин градусов и т.д.
В позиционных системах счисления количественное значение цифры зависит от ее позиции в числе.
Каждая позиционная система имеет алфавит цифр и основание. Основание системы счисления равно количеству цифр (знаков в ее алфавите) и определяет, во сколько раз различаются значения цифр соседних разрядов числа.
Таблица 1 - Позиционные системы счисления
| Система счисления | Основание | Алфавит |
| Десятичная | 10 | 0,1,2,3,4,5,6,7,8,9 |
| Двоичная | 2 | 0,1 |
| Восьмеричная | 8 | 0,1,2,3,4,5,6,7 |
| Шестнадцатиричная | 16 | 0,1,2,3,4,5,6,7,8,9, А(10),В(11),С(12),D(13),E(14),F(15) |
q-ричная СС определяется натуральным числом q1, называемым основанием системы счисления. Для представления числа х в q-ричной системе счисления его представляют в виде линейной комбинации степеней числа q:
| 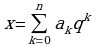
| (1) |
где ak – целые, 0≤ ak≤q
При одновременной работе с несколькими системами счисления для их различения основание системы обычно указывается в виде нижнего индекса: 235, 55510.
Рассмотрим десятичное число 73510. (пять единиц, три десятка, семь сотен).
Позиция цифры в числе называется разрядом. Разряд числа возрастает справа налево, от младших разрядов к старшим.
Число 73510 записано в свернутой форме.
В развернутой форме запись числа 73510 будет выглядеть следующим образом: 73510=7∙102 + 3∙101 + 5∙100
Число в позиционных системах счисления записывается в виде суммы числового ряда степеней основания (в данном случае 10), в качестве коэффициентов которых выступают цифры данного числа.
Для записи десятичных дробей используются разряды с отрицательными значениями степеней основания.
Например, число 235,1510 в развернутой форме будет записываться следующим образом:
235,1510 = 2∙102 + 3∙101 + 5∙100 + 1∙10-1 + 5∙10-2
В общем случае в десятичной системе запись числа А10, которое содержит n целых разрядов числа и m дробных разрядов числа, производится следующим образом:
А10=аn-1∙10n-1 +…+ a0∙100 + a-1∙10-1+ …+ a-m∙10-m
Коэффициенты аi в этой записи являются цифрами десятичного числа, которое в свернутой форме записывается следующим образом:
А10 = аn-1…a0a-1…a-m
Умножение (деление) десятичного числа на величину основания (10) приводит к перемещению запятой, отделяющей целую часть от дробной на один разряд вправо или влево.
Например,
555,5510∙10=5555,510 555,5510:10=55,55510
В двоичной системе счисления основание равно 2, алфавит состоит из двух цифр (0 и 1). Следовательно, числа в двоичной системе в развернутой форме записываются в виде суммы ряда степеней основания 2 с коэффициентами, в качестве которых выступают цифры 0 или 1.
Например, в свернутой форме запись двоичного числа выглядит следующим образом:
А2=101,012,
а развернутая:
А2 = 1∙22 + 0∙21 + 1∙20 + 0∙2-1 + 1∙2-2
В общем случае в двоичной системе запись числа А2, которое содержит n целых разрядов числа и m дробных разрядов числа, производится следующим образом:
А2=аn-1∙2n-1 +…+ a0∙20 + a-1∙2-1 + …+ a-m∙2-m
Коэффициенты аi в этой записи являются цифрами (0 или 1) двоичного числа, которое в свернутой форме записывается следующим образом:
А2=аn-1…a0a-1…a-m
Умножение или деление двоичного числа на 2 (величину основания) приводит к перемещению запятой, отделяющей целую часть от дробной на один разряд вправо или влево.
Например,
101,012 2=1010,12 101,012:2=10,1012
В системах счисления с основанием q (q-ная система счисления) числа в развернутой форме записываются в виде суммы ряда степеней основания q с коэффициентами, в качестве которых выступают цифры 0, 1, q-1.
В развернутой форме число в системе счисления с основанием q записывается следующим образом:
Аq=аn-1∙qn-1 +…+ a0∙q0 + a-1∙q-1 + …+ a-m∙q-m
Коэффициенты аi в этой записи являются цифрами числа, записанного в q–ной системе счисления.
Так, в восьмеричной системе основание равно восьми (q=8), тогда записанное в свернутой форме восьмеричное число А8=673,28 в развернутой форме будет иметь вид:
А8=6∙82 + 7∙81 + 3∙80 + 2∙8-1.
В шестнадцатеричной системе счисления записанное в свернутой форме шестнадцатеричное число А16=8A,F16 в развернутой форме будет иметь вид:
А16=8∙161 + А∙160 + F∙16-1 =8∙161 + 10∙160 + 15∙16-1
2.3.2. Кодирование чисел в различных системах счисления Преобразование чисел, представленных в двоичной, восьмеричной и шестнадцатеричной системах счисления, в десятичную СС выполняют, записывая число в развернутой форме и вычисляя его значение.
Например;
Запишем число 10,112 в развернутой форме и произведем вычисления:
10,112=1∙21+0∙20+1∙2-1+1∙2-2=1∙2+0∙1+1∙(1/2)+1∙(1/4)=2,7510
Алгоритм перевода целого десятичного числа в двоичное: последовательно выполняется деление исходного целого десятичного числа и получаемых целых частных на основание системы (2) до тех пор, пока не будет получено частное меньше делителя, то есть меньше 2. Записать полученные остатки в обратной последовательности.
Например; перевод десятичного числа 16410 в двоичную систему можно представить в табличной форме:
| Десятичное число | Делитель (основание системы) | Остаток | Цифры двоичного числа |
| 164 | 2 | 0 | a0 |
| 82 | 2 | 0 | a1 |
| 41 | 2 | 1 | a2 |
| 20 | 2 | 0 | a3 |
| 10 | 2 | 0 | a4 |
| 5 | 2 | 1 | a5 |
| 2 | 2 | 0 | a6 |
| 1 | 2 | 1 | a7 |
Таким образом, 16410=а7а6а5а4а3а2а1а0=101001002 16410=101001002
Алгоритм перевода десятичной дроби в двоичную: последовательно выполнять умножение исходной десятичной дроби и получаемых дробей на основание системы (на 2) до тех пор, пока не будет получена нулевая дробная часть или не будет достигнута требуемая точность вычислений. Получить искомую двоичную дробь, записав полученные целые части произведений в прямой последовательности.
Например; перевод десятичного числа 712,2510 в двоичную систему можно представить в виде двух таблиц:
1. Перевод целой части (71210):
| Десятичное число | Делитель (основание системы) | Остаток | Цифры двоичного числа |
| 712 | 2 | 0 | a0 |
| 356 | 2 | 0 | a1 |
| 178 | 2 | 0 | a2 |
| 89 | 2 | 1 | a3 |
| 44 | 2 | 0 | a4 |
| 22 | 2 | 0 | a5 |
| 11 | 2 | 1 | a6 |
| 5 | 2 | 1 | a7 |
| 2 | 2 | 0 | a8 |
| 1 | 2 | 1 | a9 |
Таким образом, 71210=а9а8а7а6а5а4а3а2а1а0=10110010002
2. Перевод десятичной дроби (0,2510)
| Десятичная дробь/дробная часть произведения | Множитель (основание системы) | Целая часть произведения | Цифры двоичного числа |
| 0,25 | 2 | 0 | a-1 |
| 0,50 | 2 | 1 | a-2 |
| 0,00 | 2 |
|
|
|
|
|
|
|
Таким образом, 0,2510=а-1а-2=0,012 712,2510=1011001000,012
Перевод чисел из позиционной системы с произвольным основанием p в систему с основанием q, производится по алгоритму рассмотренному выше.
Например; перевод десятичного числа 16410 в восьмеричную систему:
| Десятичное число | Делитель (основание системы) | Остаток | Цифры восьмеричного числа |
| 164 | 8 | 4 | a0 |
| 20 | 8 | 4 | a1 |
| 2 | 8 | 2 | a2 |
|
|
|
|
|
Таким образом, 16410=а2а1а0= 2448 16410=2448
Например; перевод десятичного числа 712,2510 в восьмеричную систему:
1. Перевод целой части (712):
| Десятичное число | Делитель (основание системы) | Остаток | Цифры восьмеричного числа |
| 712 | 8 | 0 | a0 |
| 89 | 8 | 1 | a1 |
| 11 | 8 | 3 | a2 |
| 1 | 8 | 1 | a3 |
|
|
|
|
|
Таким образом, 71210=а3а2а1а0=13108
2. Перевод десятичной дроби (0,25)
| Десятичная дробь/дробная часть произведения | Множитель (основание системы) | Целая часть произведения | Цифры восьмеричного числа |
| 0,25 | 8 | 2 | a-1 |
| 0,00 | 8 |
|
|
|
|
|
|
|
Таким образом, 0,2510=а-1=0,28 712,2510=1310,28
Например; перевод десятичного числа 16410 в шестнадцатиричную систему:
| Десятичное число | Делитель (основание системы) | Остаток | Цифры шестадцатиричного числа |
| 164 | 16 | 4 | a0 |
| 10 | 16 | 10(А) | a1 |
Таким образом, 16410=а1а0=А416 16410=А416
Например; перевод десятичного числа 670,2510 в шестнадцатиричную систему:
1. Перевод десятичного числа 67010:
| Десятичное число | Делитель (основание системы) | Остаток | Цифры шестадцатиричного числа |
| 670 | 16 | 14(E) | a0 |
| 41 | 16 | 9 | a1 |
| 2 | 16 | 2 | a2 |
|
|
|
|
|
Таким образом, 67010=а2а1а0=29E16
2. Перевод десятичной дроби 0,2510:
| Десятичная дробь/дробная часть произведения | Множитель (основание системы) | Целая часть произведения | Цифры шестадцатиричного числа |
| 0,25 | 16 | 4 | a-1 |
| 0,00 | 16 |
|
|
|
|
|
|
|
Таким образом, 0,2510=а-1=0,416 670,2510=29E,416
Перевод чисел из двоичной системы счисления в восьмеричную и шестнадцатеричную. Перевод чисел между системами счисления, основания которых являются степенями числа 2 (q=2n), может производиться по более простым алгоритмам. Такие алгоритмы могут применяться для перевода чисел между двоичной (q=21), восьмеричной (q=23) и шестнадцатеричной (q=24) системами счисления.
Для записи двоичных чисел используются две цифры, т.е. в каждом разряде числа возможны два варианта записи.
Решаем показательное уравнение:
2=2I , т.к. 2=21, то I=1бит. Каждый разряд двоичного числа содержит 1 бит.
Для записи восьмеричных чисел используются восемь цифр, т.е. в каждом разряде числа возможны восемь вариантов записи. Решаем показательное уравнение: 8=2I , т.к. 8=23, то I=3бит. Каждый разряд восьмеричного числа содержит 3 бита.
Алгоритм перевода двоичного числа в восьмеричное: двоичное число нужно разбить на группы по три цифры, справа налево, а затем преобразовать каждую группу в восьмеричную цифру. Если в последней левой группе окажется меньше, чем три разряда, то необходимо ее дополнить слева нулями.
Например, переведем таким способом двоичное число 1010012 в восьмеричное:
101 0012 = 1∙22+0∙21+1∙20 0∙22+0∙21+1∙20
5 1 =518
Для упрощения перевода можно заранее подготовить таблицу преобразования двоичных триад (или треплет - групп по 3 цифры) в восьмеричные цифры.
Таблица 2.3 - Таблица преобразования двоичных триад в восьмеричные цифры
| Двоичные триплеты | 000 | 001 | 010 | 011 | 100 | 101 | 110 | 111 |
| Восьмеричные цифры | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Алгоритм перевода двоичной дроби в восьмеричную: необходимо разбить дробное двоичное число на триады (триплеты) слева направо и, если в последней правой группе окажется меньше разрядов, дополнить ее справа нулями. Далее, необходимо триады заменить на восьмеричные числа.
Например, преобразуем дробное двоичное число А2=0,1101012 в восьмеричную систему счисления:
| Двоичные триады | 110 | 101 |
| Восьмеричные цифры | 6 | 5 |
Таким образом, А8=0,658 0,1101012=0,658
Для записи шестнадцатеричных чисел используются шестнадцать цифр, т.е. в каждом разряде числа возможны шестнадцать вариантов записи. Решаем показательное уравнение: 16=2I , т.к. 16=24, то I=4бит.
Каждый разряд шестнадцатеричного числа содержит 4 бита.
Алгоритм перевода целого двоичного числа в шестнадцатеричное: целлон двоичное число нужно разбить на группы по четыре цифры (квартеты), начиная справа, и, если в последней левой группе окажется меньше разрядов, дополнить ее слева нулями.
Для перевода дробного двоичного числа в шестнадцатеричное необходимо разбить его на квартеты слева направо и, если в последней правой группе окажется меньше, чем четыре разряда, то необходимо ее дополнить справа нулями.
Затем необходимо преобразовать каждую группу в шестнадцатеричную цифру, воспользовавшись для этого предварительно составленной таблицей соответствия двоичных квартетов и шестнадцатеричных цифр (самостоятельно).
Например, переведем целое двоичное число А2=1010012 в шестнадцатеричную СС:
| Двоичные квартеты: | 0010 | 1001 |
| Шестнадцатиричные цифры: | 2 | 9 |
В результате имеем, А16=2916 1010012=2916
Для того, чтобы преобразовать дробное двоичное число в шестнадцатеричную систему счисления, необходимо произвести преобразования по рассмотренным выше алгоритмам отдельно для его целой и дробной частей.
Например, переведем А2=0,1101012 в шестнадцатеричную систему счисления:
| Двоичные квартеты | 1101 | 0100 |
| Шестнадцатиричные цифры | 14(D) | 4 |
В результате имеем, А16=0,D416 0,1101012=0,D416
Алгортим перевода чисел из восьмеричной и шестнадцатеричной систем счисления в двоичную: необходимо цифры числа преобразовать в группы двоичных чисел. Для перевода из восьмеричной системы в двоичную каждую цифру числа надо преобразовать в группу из трех двоичных разрядов (треплет), а при преобразовании шестнадцатеричного числа - в группу из четырех разрядов (квартет).
Например, преобразуем дробное восьмеричное число А8=0,478 в двоичную систему счисления:
| Восьмеричные цифры: | 4 | 7 |
| Двоичные триады: | 100 | 111 |
В результате имеем, А2=0,1001112 0,478=0,1001112
Переведем целое шестнадцатеричное число А16=АВ16 в двоичную систему счисления:
| Шестнадцатиричные цифры: | 10(А) | 11(В) |
| Двоичные тетрады: | 1010 | 1011 |
В результате имеем, А2=101010112 АВ16=101010112
Задания:
Записать десятичные числа 199910, 19,9910 в развернутой форме.
Записать числа 10102, 10102, 6458, 64,58 в развернутой форме.
Записать шестнадцатиричные числа 39F16, 39,F16 в развернутой форме.
Какое основание может иметь система счисления, если в ней записаны числа 23 и 67?
Записать число 1999 в римской системе счисления.
Перевести в десятичную систему следующие числа: 1012, 1112; 118, 228
Перевести в десятичную систему следующие числа: 1А16, BF16, 9C16.
Перевести в восьмеричную и шестнадцатеричную системы счисления: 11112, 0,011112.
Перевести в двоичную систему счисления следующие числа:46,278, ЕF,1216
Сравнить числа:11012 и D16, 111112 и 228.
Автор-разработчик: Киборт А.Н. преподаватель кафедры ООД