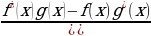209 законспектировать и выполнить задания! Прислать на почту: [email protected]
Тема: Определение производной. Формулы и правила дифференцирования
Цели урока:
ввести понятие производной;
рассмотреть формулы и правила производных
Теоретический материал (законспектировать)
Понятие производной
 Пусть
Пусть  – некоторая функция, определенная на промежутке (a; b) и
– некоторая функция, определенная на промежутке (a; b) и 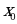 - некоторая фиксированная точка этого промежутка. Возьмем произвольное значение x из промежутка (a; b) и составим разность x -
- некоторая фиксированная точка этого промежутка. Возьмем произвольное значение x из промежутка (a; b) и составим разность x -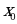 . Разность x -
. Разность x -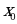 называют приращением независимой переменной (или приращением аргумента) функции
называют приращением независимой переменной (или приращением аргумента) функции  в точке
в точке 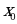 и обозначают
и обозначают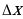 :
:
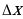 = x -
= x -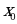 (1)
(1)
Приращением функции  в точке
в точке 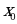 называют разность между значением функции в точке
называют разность между значением функции в точке 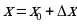 и значением функции в точке
и значением функции в точке 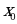 и обозначают
и обозначают  :
:
 =
= 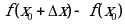 (2)
(2)
Т.к. точка 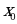 считается фиксированной, приращением функции
считается фиксированной, приращением функции 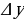 является функцией приращения аргумента
является функцией приращения аргумента 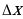 .
.
Составим отношение
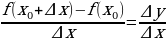 ,
,
которое также будет функцией приращения аргумента 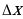 ; и рассмотрим предел этого выражения при
; и рассмотрим предел этого выражения при 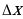 , стремящемся к нулю:
, стремящемся к нулю:
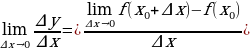 .
.
Если этот предел существует, то говорят, что функция  имеет производную в точке
имеет производную в точке 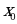 , и пишут:
, и пишут:
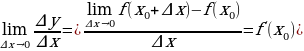 (3)
(3)
Читают: f /(x0) – (эф штрих от х0).
Число  называется производной функции в точке
называется производной функции в точке 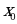 .
.
Нахождение производной называется дифференцированием функции.
Если существует предел (3), также говорят, что функция  дифференцируема в точке
дифференцируема в точке 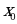 .
.
Если функция  дифференцируема в каждой точке промежутка (a; b), то говорят, что она дифференцируема в промежутке (a; b).
дифференцируема в каждой точке промежутка (a; b), то говорят, что она дифференцируема в промежутке (a; b).
Производная функции  , дифференцируемой в промежутке (a; b), сама является функцией x.
, дифференцируемой в промежутке (a; b), сама является функцией x.
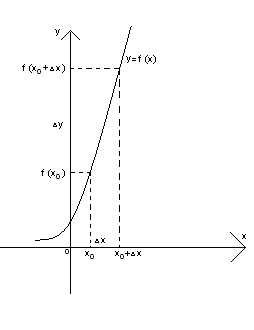
Алгоритм отыскания производной функции y = f ( x )
Чтобы вычислить производную функции  в точке
в точке 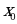 нужно:
нужно:
найти приращение функции: 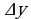 = f ( x0 +
= f ( x0 + 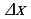 ) - f ( x0 ).
) - f ( x0 ).
найти отношение 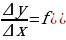 .
.
вычислить предел этого отношения: 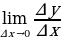 . Этот предел и есть f / ( x ).
. Этот предел и есть f / ( x ).
Производная – это «новая» функция, произведенная от данной функции по указанному правилу.
Определим производные следующих функций:
а) линейной функции 
б) квадратичной функции 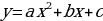
в) кубической функции 
Решение:
а). 
1. 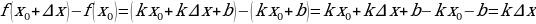
2. 
3. 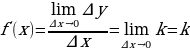 . Значит,
. Значит, 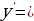
б). 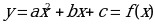
1. 
2. 
3.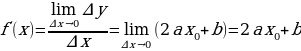 . Значит,
. Значит, 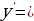
в). 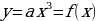
1. 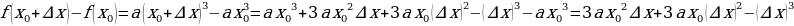 .
.
2. 
3. 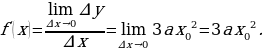 Значит,
Значит, 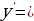
Для аргумента в первой, во второй и в третьей степени мы можем получить следующее:
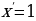


Применяя метод математической индукции, формула производной степенной функции будет выглядеть следующим образом:
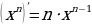
Приняв 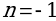 и
и 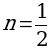 , получаются следующие формулы:
, получаются следующие формулы:
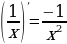 и
и 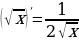
Производные элементарных функций
1.  производная постоянной величины равна нулю.
производная постоянной величины равна нулю.
2.
 , где p-любое число, в частности
, где p-любое число, в частности 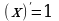 ,
,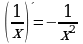 ,
, 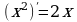 ,
,

3. 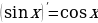 , в частности
, в частности 
4.
 , в частности
, в частности 
5.  6.
6.  7.
7. 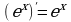 в частности,
в частности, 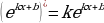 8.
8. 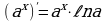 9.
9.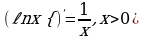 10.
10. 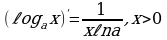 11.
11.  12.
12. 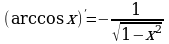 13.
13.  14.
14. 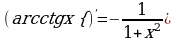
Пример: Используя формулу  найдите производные:
найдите производные:
a)
б) 
в)  ;
;
г)  ;
;
д)  ;
;
е) 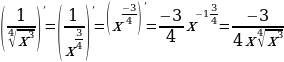 .
.
Правила дифференцирования
Практическое задание:
Дифференцирование функций (выполнить самостоятельно)
| Учебные элементы | Задания обучающей самостоятельной работы | Рекомендации к выполнению заданий |
Производная степенной функции
2. Правила дифференцирования
3. Значение производной функции в точке
4. Уравнения и неравенства | Найдите производную функции: 1. а) х6 ; б) х13 2. а) х-3 ; б) х-7 3. а)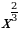 ; б) ; б) 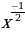 4. а) 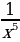 ; б) ; б) 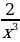 5. а) 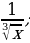 б) б) 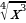
Найдите производные функций: 6. а)3х5; б)7х; в)3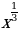 ; г) ; г) . . 7. а)5sin x; б)4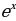 ; в)3 ; в)3  x; г)7ctg x. x; г)7ctg x.
8. а) y = 5х3 - 3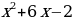 ; ; б) y = -7х-3 + 8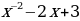 . .
9. y = x3 + 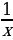 + + 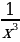 . . 10. у = 2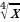 - - 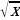 . . 11. y = 2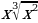 + + 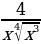 ; ; 12. a) y = 6 ; ; б) у = 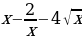 + 3. + 3.
13. а) у =x5 ln x; б) у =  . . 14. у = 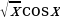 . . 15. у = (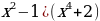 . . 16. у = 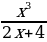 . . 17. у =  . . 18. у = 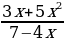 . .
Найдите значение производной функции в точке х0: 19. у = x3 – 3x + 2; х0 = -1. 20. у =  ; х0 = 9. ; х0 = 9. 21. у = 2ctg x; х0 = 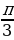 . . 22. у =  - 2x); х0 = - 2x); х0 =  . .
23. Найдите значения х, при которых значение производной функции f(x) = 2x3 – x2 равно нулю; положительно; отрицательно.
24. При каких значениях х выполняется равенство f/(x) = 2, если известно, что f(x) = 2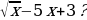 | Используйте формулу (хp)/ = p∙xp-1
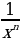 = = 

Постоянный множитель можно вынести за знак производной (с∙f(x))/ = c∙f/(x)
Производная суммы равна сумме производных
Представьте слагаемые в виде степени. (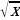 )/ = )/ = 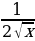 ; ;  )/ = - )/ = -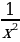
Производная произведения: (f(x)g(x))/=f/(x)g(x)+f(x)g/(x)
Производная частного:  / = / = 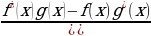
Алгоритм решения: 1.Найдите производную данной функции. 2. Подставьте в производную значение х0.
Алгоритм решения: 1. Найдите производную. 2. Разложите производную на множители. 3. Методом интервалов определите знаки производной.
|






 Пусть
Пусть  – некоторая функция, определенная на промежутке (a; b) и
– некоторая функция, определенная на промежутке (a; b) и 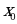 - некоторая фиксированная точка этого промежутка. Возьмем произвольное значение x из промежутка (a; b) и составим разность x -
- некоторая фиксированная точка этого промежутка. Возьмем произвольное значение x из промежутка (a; b) и составим разность x -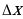 :
: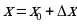 и значением функции в точке
и значением функции в точке  :
: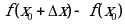 (2)
(2)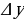 является функцией приращения аргумента
является функцией приращения аргумента 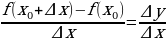 ,
,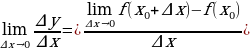 .
. 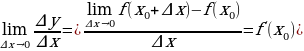 (3)
(3) называется производной функции в точке
называется производной функции в точке 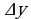 = f ( x0 +
= f ( x0 + 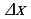 ) - f ( x0 ).
) - f ( x0 ).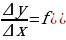 .
.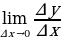 . Этот предел и есть f / ( x ).
. Этот предел и есть f / ( x ).
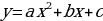


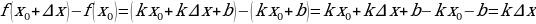

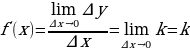 . Значит,
. Значит, 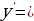
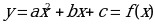

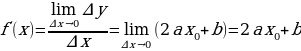 . Значит,
. Значит, 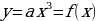
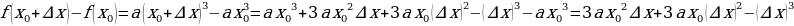 .
. 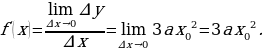 Значит,
Значит, 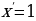

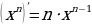
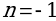 и
и 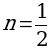 , получаются следующие формулы:
, получаются следующие формулы: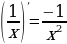 и
и 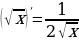
 производная постоянной величины равна нулю.
производная постоянной величины равна нулю.
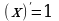 ,
,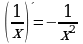 ,
, 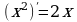 ,
, 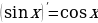 , в частности
, в частности 
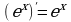 в частности,
в частности, 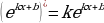 8.
8. 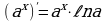 9.
9.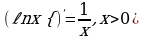 10.
10. 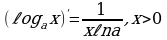 11.
11.  12.
12. 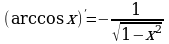 13.
13.  14.
14. 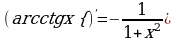
 ;
;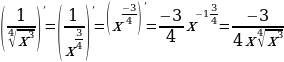 .
.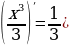
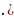
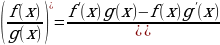

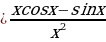
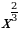 ; б)
; б) 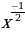
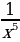 ; б)
; б) 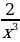
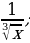 б)
б) 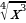
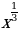 ; г)
; г) .
. 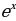 ; в)3
; в)3  x; г)7ctg x.
x; г)7ctg x. 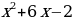 ;
; 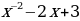 .
.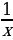 +
+ 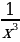 .
. 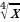 -
- 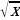 .
.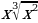 +
+ 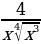 ;
; ;
;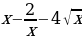 + 3.
+ 3. .
.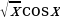 .
.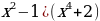 .
.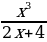 .
. .
.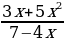 .
. ; х0 = 9.
; х0 = 9.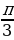 .
. - 2x); х0 =
- 2x); х0 =  .
.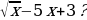
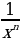 =
= 

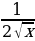 ;
; 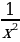
 / =
/ =