Аксиомы стереометрии и их простейшие следствия

Аксиомы стереометрии и их простейшие следствия

Урок - общественный смотр знаний по геометрии в 10 классе

Учитель математики Н.В. Руцынска я

Знания надо не только иметь, но и надо уметь ими пользоваться и уметь их показывать.

План проведения смотра знаний по геометрии в 10 классе:

• Конкурс  «Аукцион знаний»
• Конкурс «Решение заданий»
• Конкурс «Ералаш»

Первый конкурс  «Аукцион знаний»

ГЕОМЕТРИЯ

(от греч. слова geо – «Земля» и metreo – «измеряю» ) - часть математики, изучающая пространственные отношения и формы.

Впервые этот термин появился в 5 веке до н.э. в Египте и Вавилоне.

ПЛАНИМЕТРИЯ

СТЕРЕОМЕТРИЯ

(от лат.  planum  - «плоскость », др.-греч. metreo  - «измеряю» ) - раздел геометрии, в котором изучаются свойства фигур, лежащих в плоскости. Впервые этот термин встречается у древнегреческого ученого Евклида (4 век до н.э.)

(от греч. слова stereos – «объемный» и metreo – «измеряю») – раздел геометрии, в котором изучаются пространственные фигуры и их свойства

5

ГЕОМЕТРИЯ

«ЗЕМЛЕМЕРИЕ»

Т

m

М

Основные понятия стереометрии

• точка,
• прямая,
• плоскость.

А

Р

С

К



 = ( РКС)

A   , KC   , P   .

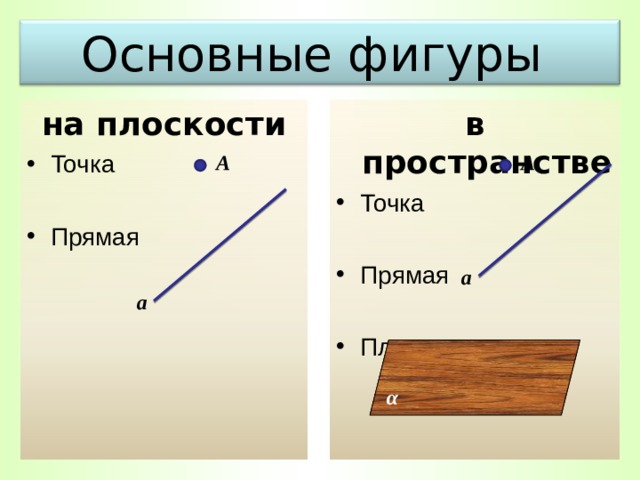
Основные фигуры

на плоскости

в пространстве

• Точка

• Точка
• Прямая
• Плоскость

• Прямая

A

A

a

a

α

  Фигура (от лат. figura – «внешний вид», «образ»). Данный термин применяется к разнообразным множествам точек.

в пространстве

на плоскости

Сведения из истории геометрии

точка – это то, что не имеет длины и ширины.

прямая – это то, что имеет длину, но не имеет ширины.

плоскость – это то, что имеет длину и ширину, но не имеет толщины.

Евклид ( III в до н.э.)

древнегреческий ученый

Аксиома

(от греч. слова axios – « ценный » ; axioma – « принятие положения » , « почет » , « уважение » , « авторитет » ) - это основное положение, самоочевидный принцип.

Впервые термин встречается у Аристотеля, использовался в « Началах » Евклида, в работах древнегреческого ученого Архимеда.

В русском языке термин появился

с Петровских времен.

Теорема

(греч. слово tereo – «исследую ») - это математическое утверждение, истинность которого устанавливается путем доказательства.

Термин употреблялся

еще Архимедом.

Сведения из истории геометрии

Гением и революционером в науке геометрии оказался великий русский математик Николай Иванович Лобачевский.

Построивший логически непротиворечивую геометрию, существенно отличную от евклидовой.

Лобачевский Н.И.

(1792-1856)

русский математик

Второй конкурс  « Решение заданий »

Аксиомы стереометрии

С 1

Какова бы ни была плоскость, существуют точки, принадлежащие этой плоскости, и точки, не принадлежащие ей.

В

(•) А   ,

(•) В и (•) С  .

А



α

С

m

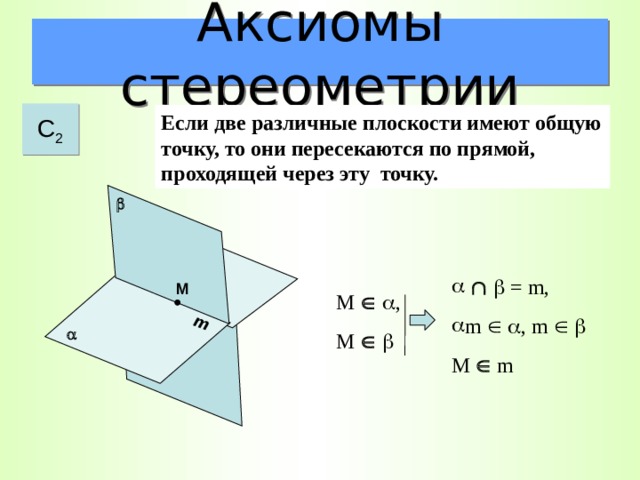
Аксиомы стереометрии

С 2

Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.



•   = m ,
• m   , m  

М  m

М

М   ,

М  



Е

Аксиомы стереометрии

С 3

Если две различные прямые имеют общую точку, то через них можно провести плоскость, и притом только одну.

a  b = O

O

α

a

b

α

m

Е

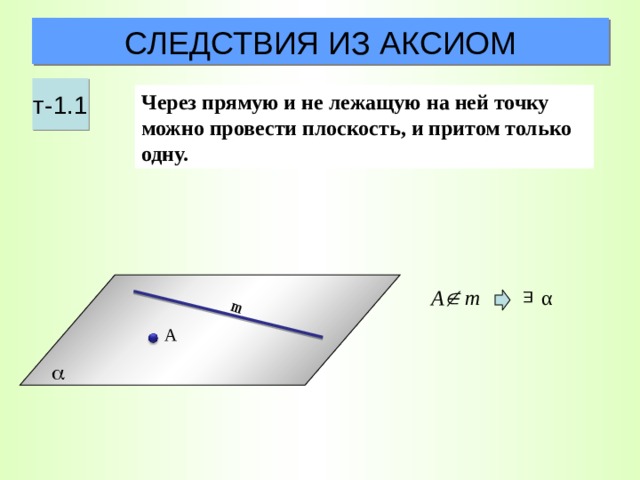
СЛЕДСТВИЯ ИЗ АКСИОМ

т-1.1

Через прямую и не лежащую на ней точку можно провести плоскость, и притом только одну.

α

А  m

А



m

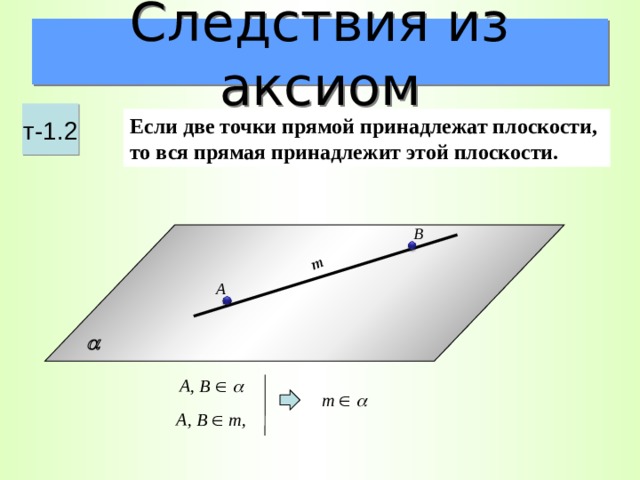
Следствия из аксиом

т-1.2

Если две точки прямой принадлежат плоскости, то вся прямая принадлежит этой плоскости.

В

А



А, В  

m  

А, В  m ,

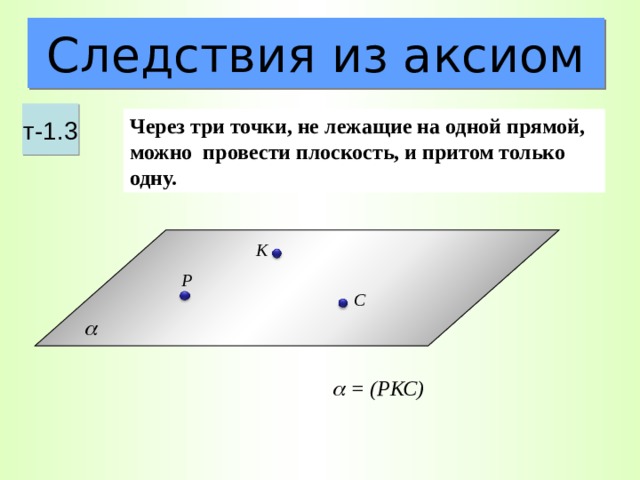
Следствия из аксиом

т-1.3

Через три точки, не лежащие на одной прямой, можно провести плоскость, и притом только одну.

К

Р

С



 = ( РКС)

I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I IIII I

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

Линейку прикладывают краем к плоской поверхности стола. Если край линейки ровный, то он всеми своими точками прилегает к поверхности стола. Если край неровный, то в каких-то местах между ним и поверхностью стола образуется просвет.

Геометрия: Учеб. Для 10-11 кл. общеобразова. учреждений / Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев и др.

23

Устойчивость - это способность сопротивляться опрокидыванию при неблагоприятных условиях эксплуатации.

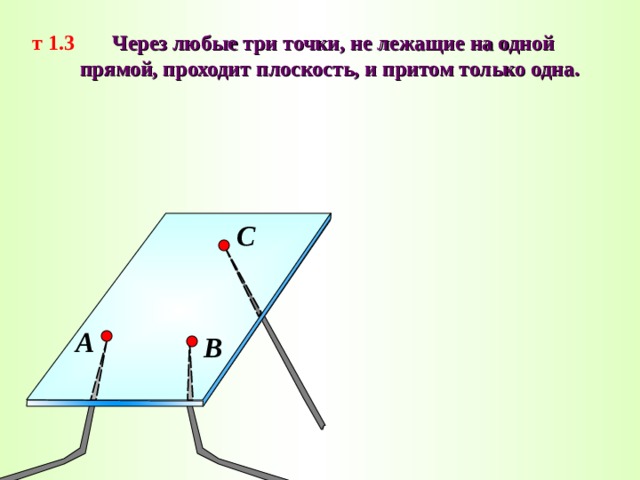
т 1.3 Через любые три точки, не лежащие на одной

прямой, проходит плоскость, и притом только одна.

С

На кнопку « i » можно нажать несколько раз.

А

В

25

Качественная фотография получится, если фотоаппарат не двигается в руках фотографа; поэтому его закрепляют на треноге – штативе.

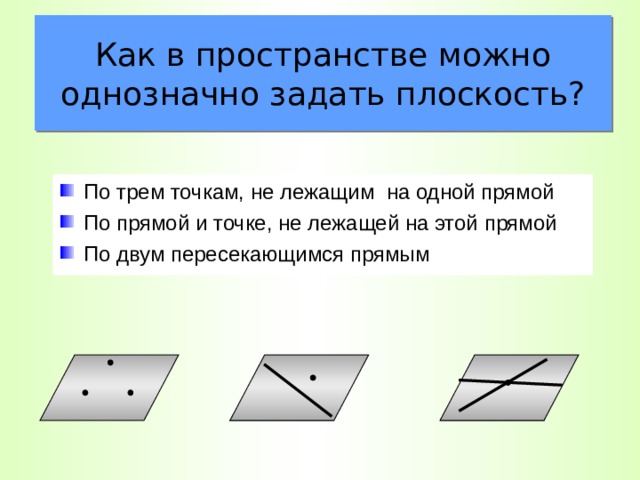
Как в пространстве можно однозначно задать плоскость?

• По трем точкам, не лежащим на одной прямой
• По прямой и точке, не лежащей на этой прямой
• По двум пересекающимся прямым