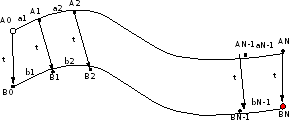Дз 15. Динамическое программирование-2. Повторение.

Динамическое программирование-2. Повторение.

1. 22-65. Исполнитель Июнь15 преобразует число на экране. У исполнителя есть две команды, которым присвоены номера:

1. Прибавить 1

2. Прибавить 5

Первая команда увеличивает число на экране на 1, вторая увеличивает его на 5. Программа для исполнителя Июнь15 – это последовательность команд. Сколько существует программ, для которых при исходном числе 2 результатом является число 26 и при этом траектория вычислений содержит число 15 и не содержит число 10?

1. 22-67. Исполнитель Июнь15 преобразует число на экране. У исполнителя есть две команды, которым присвоены номера:

1. Прибавить 1

2. Прибавить 3

Первая команда увеличивает число на экране на 1, вторая увеличивает его на 3. Программа для исполнителя Июнь15 – это последовательность команд. Сколько существует программ, для которых при исходном числе 5 результатом является число 25 и при этом траектория вычислений содержит число 15 и не содержит число 12?

1. 22-73. Исполнитель Июнь16 преобразует число на экране. У исполнителя есть три команды, которым присвоены номера:

1. Прибавить 1

2. Прибавить 2

3. Умножить на 2

Сколько существует программ, для которых при исходном числе 2 результатом является число 12 и при этом траектория вычислений содержит число 10?

1. 22-50. Исполнитель Калькулятор преобразует целое число, записанное на экране. У исполнителя две команды, каждой команде присвоен номер:

1. Прибавь 1

2. Умножь на 2

Первая команда увеличивает число на экране на 1, вторая увеличивает это число в 2 раза. Сколько существует программ, которые число 3 преобразуют в число 20 и в которых предпоследняя команда 1?

1. Запись числа 234 в системе счисления с основанием N содержит 3 цифры и оканчивается на 6. Чему равно основание системы счисления?

2. Укажите наименьшее четырёхзначное шестнадцатеричное число, двоичная запись которого содержит ровно 7 нулей. В ответе запишите только само шестнадцатеричное число, основание системы счисления указывать не нужно.

3. 9-41. У Кати есть доступ в Интернет по высокоскоростному одностороннему радиоканалу, обеспечивающему скорость получения информации 2²⁰ бит в секунду. У Сергея нет скоростного доступа в Интернет, но есть возможность получать информацию от Кати по телефонному каналу со средней скоростью 2¹³ бит в секунду. Сергей договорился с Катей, что она скачает для него данные объёмом 9 Мбайт по высокоскоростному каналу и ретранслирует их Сергею по низкоскоростному каналу. Компьютер Кати может начать ретрансляцию данных не раньше, чем им будут получены первые 1024 Кбайт этих данных. Каков минимально возможный промежуток времени (в секундах) с момента начала скачивания Катей данных до полного их получения Сергеем? В ответе укажите только число, слово «секунд» или букву «с» добавлять не нужно.

4. Рисунок размером 256 на 128 пикселей занимает в памяти 12 Кбайт (без учёта сжатия). Найдите максимально возможное количество цветов в палитре изображения.

5. 9-2-81. Производится двухканальная (стерео) звукозапись с частотой дискретизации 32 кГц и 32-битным разрешением. Результаты записи записываются в файл, сжатие данных не производится; размер полученного файла – 45 Мбайт. Определите приблизительно время записи (в минутах). В качестве ответа укажите ближайшее к времени записи целое число.

6. 6-1-100. Автомат получает на вход пятизначное число. По этому числу строится новое число по следующим правилам.

1. Складываются отдельно первая, третья и пятая цифры, а также вторая и четвёртая цифры.

2. Полученные два числа записываются друг за другом в порядке неубывания без разделителей.

Пример. Исходное число: 63 179. Суммы: 6 + 1 + 9 = 16; 3 + 7 = 10. Результат: 1016.

Укажите наименьшее число, при обработке которого автомат выдаёт результат 723.

1. Придумать алгоритм решения, используя динамическое программирование, и написать программу

Гоночная трасса состоит из двух основных дорог и нескольких переездов, позволяющих перейти с одной дороги на другую.

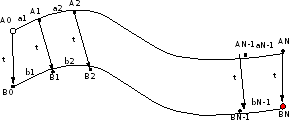
На всех участках, включая переезды, движение разрешено только в одну сторону, поэтому переезд возможен только с дороги A на дорогу B. Гонщик стартует в точке A₀ и должен финишировать в точке B_N. Он знает, за какое время сможет пройти каждый участок пути по каждой дороге, то есть время прохождения участков A₀A₁, A₁A₂, ..., A_N-1A_N, B₀B₁, B₁B₂, ..., B_N-1B_N. Время прохождения всех переездов A₀B₀, A₁B₁, ..., A_NB_N одинаково и известно гонщику. Необходимо определить, за какое минимальное время гонщик сможет пройти трассу.

Напишите эффективную, в том числе по используемой памяти, программу для решения этой задачи. Перед текстом программы кратко опишите алгоритм решения и укажите язык программирования и его версию.

Входные данные

В первой строке задаётся количество участков трассы N. Во второй строке задаётся целое число t – время (в секундах) прохождения каждого из переездов A₀B₀, A₁B₁, …, A_NB_N. В каждой из последующих N строк записано два целых числа a_i и b_i, задающих время (в секундах) прохождения очередного участка на каждой из дорог. В первой из этих строк указывается время прохождения участков A₀A₁ и B₀B₁, во второй – A₁A₂ и B₁B₂ и т. д.

Пример входных данных

3

20

320 150

200 440

300 210

Выходные данные

Программа должна напечатать одно целое число: минимально возможное

время прохождения трассы (в секундах).

Пример выходных данных для приведённого выше примера входных данных

750