Сердюкова Елена Николаевна
МБОУ «Октябрьская средняя школа № 2»
Электронная почта: [email protected]
Телефон:8 917 831 75 81.
Графический приём введения понятия «процент» в 5 классе.
В статье рассматривается графический прием введения понятия «процент». Основной целью, которой является отработка умения соотносить дробь с процентами, используя графическое изображение.
У учителя может возникнуть вопрос: а как ввести понятия «процент» так, чтобы его усвоил каждый ребенок? Что ж, если таких задач учитель не найдет, то ему придется самому сочинить их. По нашему мнению, в таких случаях целесообразно использовать графический прием введения данного понятия.
Введение процентов опирается на предметно практическую деятельность школьников, на геометрическую наглядность и геометрическое моделирование. С самого начала освоения понятия учащиеся выполняют много заданий, в которых требуется заштриховать, закрасить, начертить, вырезать часть фигуры. Широко используются рисунки и чертежи, помогающие разобраться в задаче и увидеть путь решения.
Предлагаем графические задачи как одного из средств организации деятельностного подхода на уроках математики.
Начинаю обсуждение с учащимся нового понятия.
- Знают ли, что такое процент?
- Где в практической деятельности встречались с понятием «процент»?
Запись в тетради: Один процент (%) - это одна сотая часть.
Кроме того, при сдаче ОГЭ требуются знания, связанные с процентами, а среди заданий экзамена есть задачи на процентные вычисления.
Понятие «процент» в 5 классе вводится после темы «обыкновенные дроби». Дети владеют навыками выделения части из целого с помощью рисунка. Поэтому без труда изображают квадрат со стороной 10 клеток на 10 и выделяют 1/100 часть квадрата по просьбе учителя. Остается сформулировать и озвучить, что 1\100 часть называют «процентом».
Следующей задачей становиться изображение 2% (дети закрашивают 2 клеточки) и отвечают на вопросы учителя: - 2% это какая часть целого? (2/100) т.д.
Затем детям предлагается изобразить такой же квадрат и разделить его на две равные части и закрасить одну. После чего на доске дети показывают различные варианты деления квадрата на пополам. Какая дробь соответствует закрашенной части квадрата? (1/2)
Посчитайте, сколько клеток в 1 части. (50) Какой вывод вы можете сделать, согласно первой задачи?
Представление о понятии « процент», формирую с помощью графических изображений. Приведу примеры графических задач по введению понятия «Процент».
Изобразите квадрат со стороной 10 клеток на 10.
Сколько всего клеток внутри квадрата? (100)
Закрасьте 1 клетку.
Какая часть квадрата закрашена? (Одна сотая часть)
Запишите эту дробь в виде обыкновенной дроби. (1/100)
1/100 по латыни «про центум» и обозначается 1%.
Закрасьте 10 клеточек в данном квадрате.
Какую часть составляет закрашенная часть ? 10/100
Сколько это процентов? 10%
Начертите такой же квадрат. Разделите его на две равные части.




Дети предлагают различные варианты деления квадрата на две части.
Закрасьте ½ часть.
Посчитайте, сколько клеток содержится в ½ части? 50
Сколько процентов составляет закрашенная часть? 50%
Что вы можете сказать об ½ и 50%? Что они равны.
Разделите квадрат на 4 равные части , выделите ¼ часть.
Сколько процентов составляет дробь ¼? 25%
Сколько частей осталось незакрашено? ¾
Сколько % соствавляет дробь ¾? 75%
С помощь вашего квадрата определите 5% это …, 20%=
Закрепление .
Записать проценты в виде обыкновенной дроби, затем в виде десятичной.
Пример. 12%=12/100=0,12
Обратное задание: десятичную дробь записать в виде процентов.
Приведем примеры нескольких таких задач.
В результате еще до решения основных задач на проценты, учащиеся прочно овладевают достаточно большим набором фактов, которые помогают им в дальнейшем при изучении как темы проценты, так и математики в целом. Так, они усваивают некоторые «эквиваленты»:
25 % величины – это 1/4 этой величины;
половина некоторой величины – это ее 50 %;
30 % величины втрое больше, чем ее 10 % и т.п.
Ребята учатся сравнивать доли величины, заданные разными способами:
При изучении этого материала нужно сначала объяснить учащимся, что такое сотая часть числа (например, сотая часть метра – это сантиметр, сотая часть рубля - копейка, сотая часть центнера – килограмм) надо отметить, что к этому времени учащиеся уже прошли деление и дроби и у них не возникнет проблем.
Также можно предложить учащимся задание на перевод обыкновенных и десятичных дробей в проценты, так как это часто вызывает трудности.
Задача №1.2
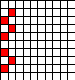
Даны квадраты (см. рис. 1), ответить на вопросы.
Какая часть квадрата заштрихована?
Выразите заштрихованную часть десятичной дробью.
Сколько процентов квадрата заштриховано?
Сколько процентов квадрата не заштриховано?



№1 Один процент числа – это его сотая часть. Например, один процент числа 300 равен сотой части числа 300, т.е. 300:100=3. Чему равен один процент числа 4800?
№2 Напоминаем: один процент числа – это его сотая часть. Чему равен один процент числа 72000?
№3 Вспомни: один процент числа равен его сотой части. Один процент обозначается так: 1%. Чему равен 1% числа 400?
№4 Чему равен 1% от 6700? Чему равны 2% от 6700?
№5 Что больше, 1% числа 200 или 5% числа 100?
№6 Прибор стоил 120 рублей. Он подешевел на 10 %. На сколько рублей подешевел прибор? Сколько рублей он теперь стоит?
№7 1% числа равен 20. Чему равно все число?
Это можно узнать так: 20 × 100 = 2000 (ведь если 20 – это сотая часть числа, то само это число в 100 раз больше, чем 20).
1% числа равен 30. Чему равно все число?
№8 1% числа равен 75. Чему равно все число?
№9 2% числа равны 40. Чему равно все число?
Решая такие графические задачи в течение продолжительного времени, учащиеся научатся решать эти задачи и привыкнут к понятию процента, им легче будет усвоить и решение трех основных задач на проценты.
Многолетний опыт применения предлагаемой методики свидетельствует, что ученики не испытывают страха перед задачами, связанные с понятием «процент», свободно и легко овладевают приемами составления и решения связок и в конечном итоге поднимаются на качественно новую ступень видения темы в целом.






















