
Иоганн Бернулли

Цели урока:
- общеобразовательные: обеспечить повторение, обобщение и систематизацию знаний по теме «Графики функций, содержащие знак модуля»; создать условия контроля усвоения знаний и умений.
- развивающие: способствовать формированию умений применять приёмы обобщения, сравнения, выделения главного; развитию математического кругозора, мышления, речи, внимания, памяти.
- воспитательные: содействовать воспитанию интереса к математике, активности, организованности, формировать положительную мотивацию учения, развивать учебно-познавательную деятельность, коммуникативность.


- Область определения функции y= ( x² + 3x – 4) × | x – 7 |
x – 7
a) x ≥ 0 ; б) х – любое число; в) х ≠ -7; х ≠ 7; г) х ≠ 7.

- Область определения функции y= ( x² + 3x – 4) × | x – 7 |
x – 7
a) x ≥ 0 ; б) х – любое число; в) х ≠ -7; х ≠ 7; г) х ≠ 7.

- Область определения функции y= ( x² + 3x – 4) × | x – 7 |
x – 7
a) x ≥ 0 ; б) х – любое число; в) х ≠ -7; х ≠ 7; г) х ≠ 7.
2. Функция y = x² - 10x +21 имеет нули
а) 7; 3 б) -7; 3 в) 7; -3 г) -7; -3.

- Область определения функции y= ( x² + 3x – 4) × | x – 7 |
x – 7
a) x ≥ 0 ; б) х – любое число; в) х ≠ -7; х ≠ 7; г) х ≠ 7.
2. Функция y = x² - 10x +21 имеет нули
а) 7; 3 б) -7; 3 в) 7; -3 г) -7; -3.

- Область определения функции y= ( x² + 3x – 4) × | x – 7 |
x – 7
a) x ≥ 0 ; б) х – любое число; в) х ≠ -7; х ≠ 7; г) х ≠ 7.
2. Функция y = x² - 10x +21 имеет нули
а) 7; 3 б) -7; 3 в) 7; -3 г) -7; -3.
- Вершиной параболы y= x² - 4x – 5 является точка
а) (2; 9) б) ( -2; 9) в) ( 2; -9) г) ( -2; -9).

- Область определения функции y= ( x² + 3x – 4) × | x – 7 |
x – 7
a) x ≥ 0 ; б) х – любое число; в) х ≠ -7; х ≠ 7; г) х ≠ 7.
2. Функция y = x² - 10x +21 имеет нули
а) 7; 3 б) -7; 3 в) 7; -3 г) -7; -3.
- Вершиной параболы y= x² - 4x – 5 является точка
а) (2; 9) б) ( -2; 9) в) ( 2; -9) г) ( -2; -9).
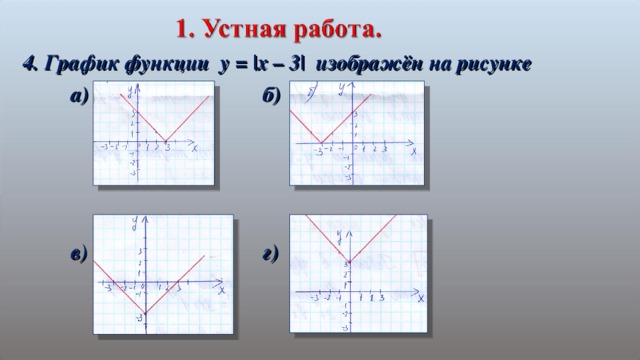
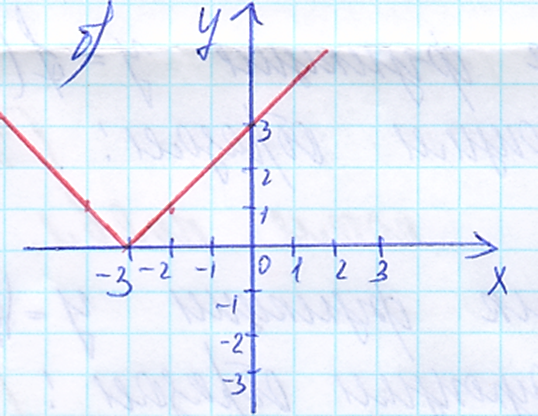
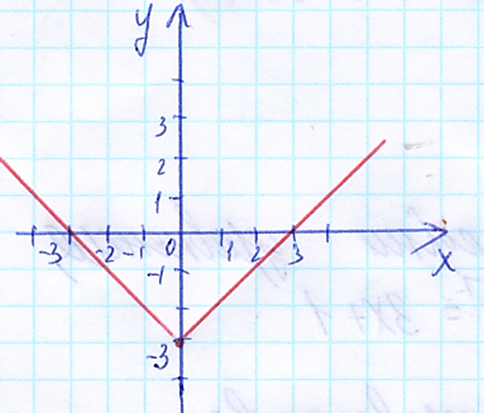
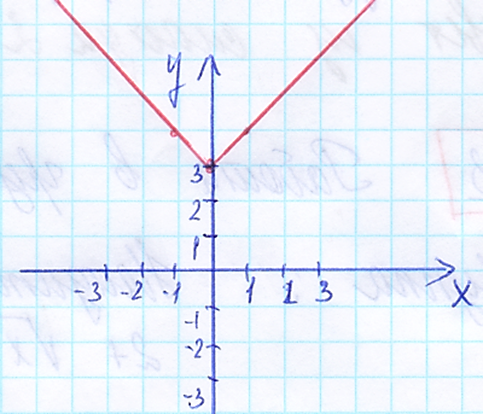
4. График функции y = |x – 3| изображён на рисунке
а) б)
в) г)
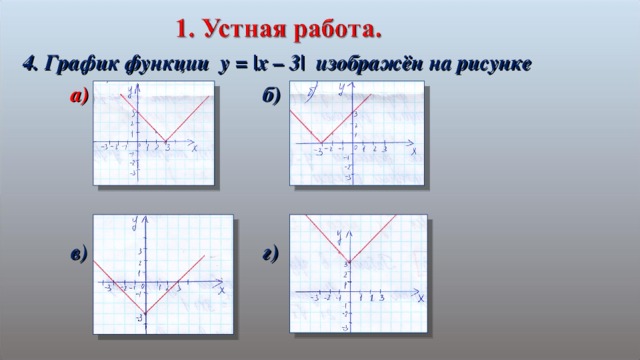
4. График функции y = |x – 3| изображён на рисунке
а) б)
в) г)

5. Упростить выражение √ х² + 8х + 16
а) упростить нельзя; б) √ (х + 4)² ; в) х + 4 г) | x + 4 | .

5. Упростить выражение √ х² + 8х + 16
а) упростить нельзя; б) √ (х + 4)² ; в) х + 4 г) | x + 4 | .

5. Упростить выражение √ х² + 8х + 16
а) упростить нельзя; б) √ (х + 4)² ; в) х + 4 г) | x + 4 | .
6. Нулями подмодульных выражений для функции
y= |3x-6| + 2|x+1| - ½ |7x+21| являются числа
а) 3; -1; 2 б) -3; -1; 2 в) -2; -½; 3 г) -3; -½; 2.

1. Устная работа.
5. Упростить выражение √ х² + 8х + 16
а) упростить нельзя; б) √ (х + 4)² ; в) х + 4 г) | x + 4 | .
6. Нулями подмодульных выражений для функции
y= |3x-6| + 2|x+1| - ½ |7x+21| являются числа
а) 3; -1; 2 б) -3; -1; 2 в) -2; -½; 3 г) -3; -½; 2.

5. Упростить выражение √ х² + 8х + 16
а) упростить нельзя; б) √ (х + 4)² ; в) х + 4 г) | x + 4 | .
6. Нулями подмодульных выражений для функции
y= |3x-6| + 2|x+1| - ½ |7x+21| являются числа
а) 3; -1; 2 б) -3; -1; 2 в) -2; -½; 3 г) -3; -½; 2.
7. Сколько точек пересечения имеют графики функций
y= x²+4x-3 и y= 9 .
а) 1; б) 3; в) ни одной; г) 2.

5. Упростить выражение √ х² + 8х + 16
а) упростить нельзя; б) √ (х + 4)² ; в) х + 4 г) | x + 4 | .
6. Нулями подмодульных выражений для функции
y= |3x-6| + 2|x+1| - ½ |7x+21| являются числа
а) 3; -1; 2 б) -3; -1; 2 в) -2; -½; 3 г) -3; -½; 2.
7. Сколько точек пересечения имеют графики функций
y= x²+4x-3 и y= 9 .
а) 1; б) 3; в) ни одной; г) 2.
![5. Упростить выражение √ х² + 8х + 16 а) упростить нельзя; б) √ (х + 4)² ; в) х + 4 г) | x + 4 | . 6. Нулями подмодульных выражений для функции y= |3x-6| + 2|x+1| - ½ |7x+21| являются числа а) 3; -1; 2 б) -3; -1; 2 в) -2; -½; 3 г) -3; -½; 2. 7. Сколько точек пересечения имеют графики функций y= x²+4x-3 и y= 9 . а) 1; б) 3; в) ни одной; г) 2. 8. Множество значений функции y= 8-x² . а) (- ∞ ; 8 ] б) (8; +∞) в) ( - ∞; 8) г) [ 8; + ∞).](https://fhd.multiurok.ru/f/e/2/fe2ce08bf78c5e991518eb50dec7ba18a1547f78/img_phpLriBs3_Elektivnyj-kurs-modul_0_17.jpg)
5. Упростить выражение √ х² + 8х + 16
а) упростить нельзя; б) √ (х + 4)² ; в) х + 4 г) | x + 4 | .
6. Нулями подмодульных выражений для функции
y= |3x-6| + 2|x+1| - ½ |7x+21| являются числа
а) 3; -1; 2 б) -3; -1; 2 в) -2; -½; 3 г) -3; -½; 2.
7. Сколько точек пересечения имеют графики функций
y= x²+4x-3 и y= 9 .
а) 1; б) 3; в) ни одной; г) 2.
8. Множество значений функции y= 8-x² .
а) (- ∞ ; 8 ] б) (8; +∞) в) ( - ∞; 8) г) [ 8; + ∞).
![5. Упростить выражение √ х² + 8х + 16 а) упростить нельзя; б) √ (х + 4)² ; в) х + 4 г) | x + 4 | . 6. Нулями подмодульных выражений для функции y= |3x-6| + 2|x+1| - ½ |7x+21| являются числа а) 3; -1; 2 б) -3; -1; 2 в) -2; -½; 3 г) -3; -½; 2. 7. Сколько точек пересечения имеют графики функций y= x²+4x-3 и y= 9 . а) 1; б) 3; в) ни одной; г) 2. 8. Множество значений функции y= 8-x² . а) (- ∞ ; 8 ] б) (8; +∞) в) ( - ∞; 8) г) [ 8; + ∞).](https://fhd.multiurok.ru/f/e/2/fe2ce08bf78c5e991518eb50dec7ba18a1547f78/img_phpLriBs3_Elektivnyj-kurs-modul_0_18.jpg)
5. Упростить выражение √ х² + 8х + 16
а) упростить нельзя; б) √ (х + 4)² ; в) х + 4 г) | x + 4 | .
6. Нулями подмодульных выражений для функции
y= |3x-6| + 2|x+1| - ½ |7x+21| являются числа
а) 3; -1; 2 б) -3; -1; 2 в) -2; -½; 3 г) -3; -½; 2.
7. Сколько точек пересечения имеют графики функций
y= x²+4x-3 и y= 9 .
а) 1; б) 3; в) ни одной; г) 2.
8. Множество значений функции y= 8-x² .
а) (- ∞ ; 8 ] б) (8; +∞) в) ( - ∞; 8) г) [ 8; + ∞).

9. График функции y = f (|x|) получен из y = f (x)
а) при х ≥ 0 график остаётся без изменений;
б) при х ˂ 0 полученная часть графика отображается симметрично относительно оси 0 Y .
10. График функций y = |f(x)| получен из y = f(x) c ледующим образом
а) часть графика, лежащая выше оси ОХ сохраняется;
б) часть графика, лежащая ниже оси ОХ симметрично отображается относительно оси О X .




Леонард Эйлер

Найдите корень уравнения. 2 + √ х² +2х + 1 = 3х + 1
1. Свернуть подкоренное выражение по формулам сокращённого умножения.
2. Используя свойство √ а² = | a | , преобразовать уравнение.
3. Привести уравнение к виду | f(x) | = g (x).
4 . В одной системе координат построить графики функций
y=|f (x)|, y= g(x).
5 . Найти абсциссу точки пересечения графиков.

Николай Иванович Лобачевский

X € ( -2; 4)
Y=4
при х € [ 2; +∞)

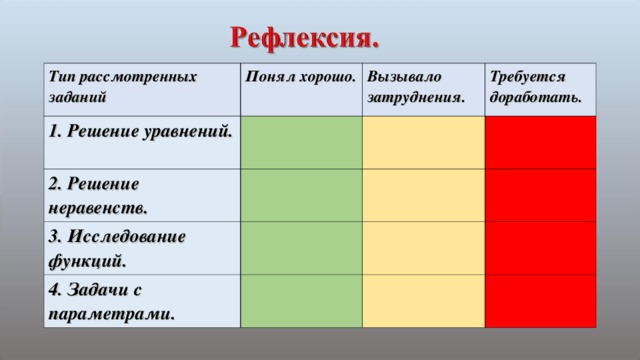
Тип рассмотренных заданий
Понял хорошо.
1. Решение уравнений.
Вызывало затруднения.
2. Решение неравенств.
Требуется доработать.
3. Исследование функций.
4. Задачи с параметрами.







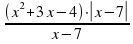
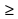
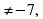 х
х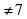 ; г) х
; г) х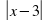 изображен на рисунке
изображен на рисунке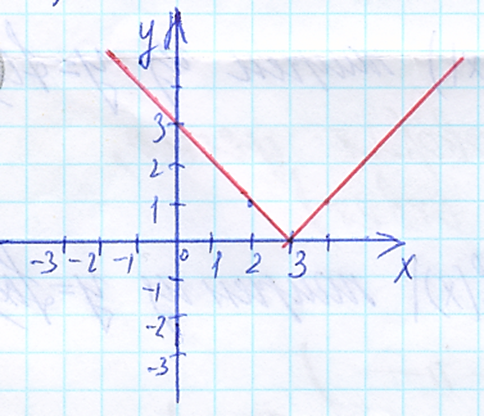
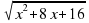
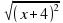 ; в) х+4; г)
; в) х+4; г) 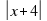
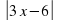 +
+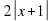 -
-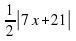 являются числа а) 3; -1; 2 б) -3; -1; 2 в) -2; -
являются числа а) 3; -1; 2 б) -3; -1; 2 в) -2; -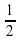 ; 3 г)-3; -
; 3 г)-3; -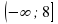 б)
б) 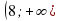 в)
в)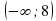 г)
г)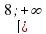
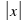 ) получен из
) получен из 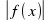 получен из
получен из 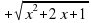 =3х+1
=3х+1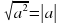 , преобразовать уравнение;
, преобразовать уравнение;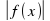 =
= 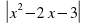
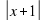 +
+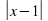 -2
-2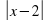
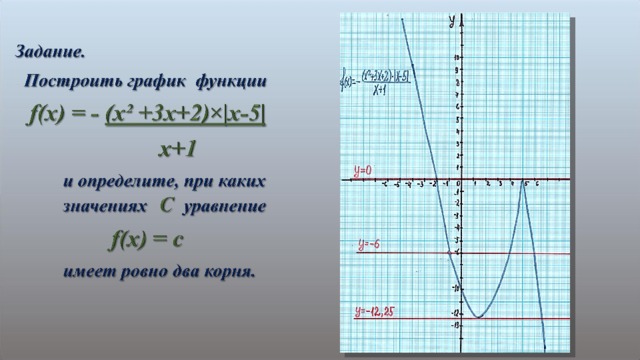
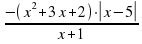 и определите, при каких значениях параметра с уравнение f(x)=c имеет ровно два корня.
и определите, при каких значениях параметра с уравнение f(x)=c имеет ровно два корня.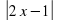
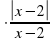 =0
=0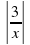 -2
-2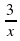 +
+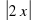 и определите, при каких значениях а этот график имеет ровно одну общую точку с прямой
и определите, при каких значениях а этот график имеет ровно одну общую точку с прямой 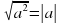 , преобразовать уравнение;
, преобразовать уравнение;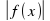 =
= 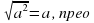 бразовать уравнение;
бразовать уравнение;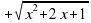 =3х+1
=3х+1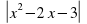
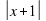 +
+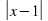 -2
-2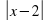
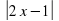
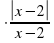 =0
=0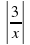 -2
-2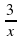 +
+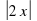 и определите, при каких значениях а этот график имеет ровно одну
и определите, при каких значениях а этот график имеет ровно одну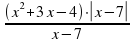
 х
х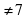 ; г) х
; г) х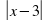 изображен на рисунке (слайд)
изображен на рисунке (слайд)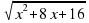
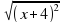 ; в)х+4; г)
; в)х+4; г) 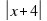
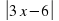 +
+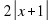 -
-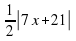 являются числа а) 3; -1; 2 б) -3; -1; 2 в) -2; -
являются числа а) 3; -1; 2 б) -3; -1; 2 в) -2; -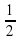 ; 3 г)-3; -
; 3 г)-3; -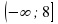 б)
б) 
















![5. Упростить выражение √ х² + 8х + 16 а) упростить нельзя; б) √ (х + 4)² ; в) х + 4 г) | x + 4 | . 6. Нулями подмодульных выражений для функции y= |3x-6| + 2|x+1| - ½ |7x+21| являются числа а) 3; -1; 2 б) -3; -1; 2 в) -2; -½; 3 г) -3; -½; 2. 7. Сколько точек пересечения имеют графики функций y= x²+4x-3 и y= 9 . а) 1; б) 3; в) ни одной; г) 2. 8. Множество значений функции y= 8-x² . а) (- ∞ ; 8 ] б) (8; +∞) в) ( - ∞; 8) г) [ 8; + ∞).](https://fhd.multiurok.ru/f/e/2/fe2ce08bf78c5e991518eb50dec7ba18a1547f78/img_phpLriBs3_Elektivnyj-kurs-modul_0_17.jpg)
![5. Упростить выражение √ х² + 8х + 16 а) упростить нельзя; б) √ (х + 4)² ; в) х + 4 г) | x + 4 | . 6. Нулями подмодульных выражений для функции y= |3x-6| + 2|x+1| - ½ |7x+21| являются числа а) 3; -1; 2 б) -3; -1; 2 в) -2; -½; 3 г) -3; -½; 2. 7. Сколько точек пересечения имеют графики функций y= x²+4x-3 и y= 9 . а) 1; б) 3; в) ни одной; г) 2. 8. Множество значений функции y= 8-x² . а) (- ∞ ; 8 ] б) (8; +∞) в) ( - ∞; 8) г) [ 8; + ∞).](https://fhd.multiurok.ru/f/e/2/fe2ce08bf78c5e991518eb50dec7ba18a1547f78/img_phpLriBs3_Elektivnyj-kurs-modul_0_18.jpg)























