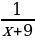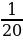Конспект урока алгебры на тему «Решение задач на совместную работу»
Тип урока: урок усвоения новых знаний.
Цели урока: Создать условия для изучения темы «Решение задач на совместную работу»; для формирования умений и навыков в составлении дробно-рациональных уравнений к этому типу задач; для развития математического мышления.
УУД: личностные – внимательно слушают, вступать в диалог; проявляют уважительное отношение к чужому мнению;
метапредметные – изучают и применяют алгоритм решения подобных задач на совместную работу;
предметные – приобретают практические навыки решения задач на совместную работу.
Актуализация. Беседа с классом:
- Какие типы задач мы уже можем решать с помощью дробных рациональных уравнений? (на движение по суше, движение по воде)
– Какую известную из курса физики формулу применяют при решении задач на движение? (S=v·t)
– Какие величины обозначены буквами S, v , t? (путь, скорость, время)
– Как зная пройденный путь и скорость найти время движения? ( t=s/v)
– Как зная пройденный путь и время найти скорость движения? (v=s/t)
- Как найти среднюю скорость при движении на нескольких участках? ((vср.=sобщ./tобщ.)
- Составить уравнение к задаче
Первую половину пути автомобиль проехал со скоростью 90 км/ ч, а вторую- со скоростью- 110 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. (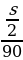 +
+ 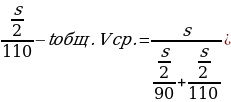
Изучение нового материала.
Внимательно прочитайте тексты задач.
| ОГЭ В-29 №21 Первая труба пропускает на 16 литров воды в минуту меньше, чем вторая труба. Сколько литров воды в минуту пропускает первая труба, если резервуар объёмом 105 литров она заполняет на 4 минуты дольше, чем вторая труба? |
Две трубы наполняют бассейн за 8 часов 45 минут. Если бы только первая труба наполняла бассейн, то он наполнился бы за 21 час. За сколько часов наполняет бассейн вторая труба? |
А) Составим таблицу для решения 1 задачи
|
| Объём работы (л) | Скорость заполнения (л/мин) | Время заполнения (мин) | Дополнительное условие |
| Первая труба | 105 | Х | 105/Х | Заполняет на 4 минуты дольше |
| Вторая труба | 105 | Х+16 | 105/Х+16 |
|
Составим уравнение к первой задачи : 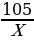 -
- 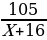 = 4 – это задача на производственную тему.
= 4 – это задача на производственную тему.
Б) Составим таблицу для решения 2задачи. Эта задача на совместную работу. Поэтому введём следующие обозначения.
А – работа, t – время выполнения работы, р –производительность труда (количество работы за некоторое количество времени). Р общ = 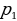 +
+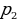 , Р = А / t =
, Р = А / t =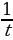
|
| Совместное время работы, ч | Раздельное время работы, ч | Вся работа | Производительность раздельная | Производительность совместная |
| I |
8 часов 45 минут =8,75 | 21 | 1 | 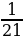
|
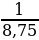
|
| II | Х | 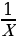
|
Р общ = 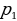 +
+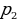 , тогда
, тогда 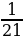 +
+ 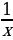 =
= 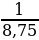 , откуда х = 15 ч.
, откуда х = 15 ч.
Итак, обратим внимание на различие в подходах к решению этих задач.
Закрепление материала.
Работа в парах. Решите задачу.
Двое рабочих, работая вместе, могут выполнить производственное задание за 20 дней. За сколько дней может выполнить задание каждый из них, работая самостоятельно, если одному из них для этого надо на 9 дней больше, чем другому?
Проверим:
|
| Совместное время работы, ч | Раздельное время работы, ч | Вся работа | Производительность раздельная | Производительность совместная |
| I |
20 | Х+9 |
1 | 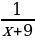
|
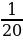
|
| II | Х | 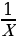
|
Ответ: 36 и 45 дней
Домашнее задание и подведение итогов урока.
- Как различить задачи на производственную тему и на совместную работу?
– Как решать задачи на совместную работу?
– По какой формуле можно найти время совместной работы?
– Что было саамы легким?
– Что было самым трудным?
Дома: Учебник № 941, 966 решить задачи .ОГЭ В-29 №6-7, 9-11







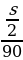 +
+ 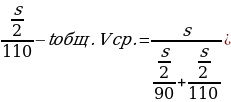
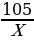 -
- 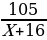 = 4 – это задача на производственную тему.
= 4 – это задача на производственную тему.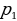 +
+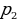 , Р = А / t =
, Р = А / t =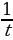
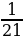
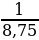
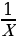
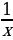 =
=