Трофимова Ирина Николаевна, учитель математики,
МБОУ СОШ с.Первомайское Михайловского района Приморского края.
Работа представляет собой конспект открытого урока по математике в 9 классе по теме: «Определение арифметической прогрессии. Формула n-го члена арифметической прогрессии.» по учебнику Ю.Н.Макарычева и др.
Урок направлен на изучение нового материала через включение учащихся в активную деятельность. Начало урока - это повторение и закрепление пройденного материала. Ознакомление с легендой о шахматной доске подводит учащихся к ознакомлению с новым материалом. Они узнают определение арифметической прогрессии, разности прогрессии, выводят формулу n-го члена арифметической прогрессии и учатся ее применять. Материал представлен в подробном виде: с решениями, ответами, что позволяет учителю сэкономить время для подготовки к уроку по данной теме, распланировать этапы урока, применить различные виды деятельности. Учит грамотно оформлять решение задач. Использованные на уроке четверостишия, написанные самим учителем, концентрируют внимание учащихся и вносят оживление в процесс деятельности. Работа будет полезна для начинающих педагогов.
АЛГЕБРА 9 класс
Тема: Определение арифметической прогрессии. Формула n- го члена арифметической прогрессии.
Среди чисел существует
Такое совершенство и согласие,
Что нам надо размышлять
Дни и ночи
Над их удивительной закономерностью. /
/Стевин /
I. Сообщение темы и цели урока.
Сегодня на уроке мы познакомимся с новым понятием:
«Арифметическая прогрессия».
Цель урока:
1- Ввести определение арифметической прогрессии;
2- Уметь находить разность арифметической прогрессии и знать, как она обозначается;
3- Получить формулу n -го члена арифметической прогрессии, уметь ее применять.
II. Повторение и закрепление пройденного материала.
1.Устная фронтальная работа с классом.
1) Какой член последовательности (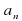 ) следует за:
) следует за:
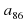 ;
; 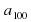 ;
; 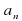 ;
; 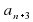 ;
;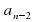 ;
; 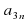
2) Какой член последовательности (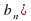 предшествует:
предшествует:
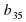 ;
; 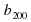 ;
; 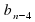 ;
; 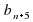 ;
; 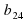
3) Назовите члены последовательности ( ), расположенные между:
), расположенные между:
а) 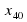 и
и 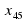 б)
б)  и
и 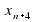 в)
в) 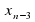 и
и 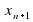
(Задания для устного счета написаны на карточках)
2. У доски во время устного счета работают 3 ученика:
(выполняют задания на повторение к экзаменам из домашней работы)
1) упростить выражение: ( 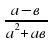 ─
─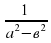 ∙
∙ 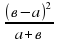 ) :
) : 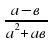
Решение. 1)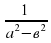 ∙
∙ 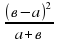 =
=  ; 2)
; 2) 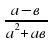 ─
─  =
= ; 3)
; 3)  :
: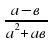 =
= 
Ответ:  .
.
2) решить биквадратное уравнение. 4 5х² + 1 = 0
5х² + 1 = 0
Решение. Введем новую переменную у = х². Получим квадратное уравнение: 4у²─5у +1= 0.
Его корни у = 1 и у = .Тогда х² = 1 (
.Тогда х² = 1 ( = 1,
= 1,  = ─1) и х² =
= ─1) и х² = (
( =
= ,
,  = ─
= ─  ).
).
Ответ : -1; ─ ;
;  ;1.
;1.
3) разгадывание кроссворда на повторение.
Кроссворд.
1.Уравнение четвертой степени (биквадратные).
2. График функции обратной пропорциональности (гипербола).
3. Формула, выражающая любой член последовательности, начиная с некоторого, через предыдущие (рекуррентная).
4. Название функции, графиком которой является парабола (квадратичная).
5.Число слагаемых при раскрытии квадрата разности (три).
6. График, для построения которого достаточно двух точек (прямая).
7. Число корней квадратного уравнения, если дискриминант равен нулю (один).
8. Значение переменной, которое обращает уравнение в верное равенство (корень).
9. Что находят по формуле b²- 4ас ? (дискриминант).
| 6П |
|
|
|
|
|
|
| 1 |
|
|
|
|
| Р |
|
|
|
|
|
|
| 7О |
|
|
|
|
| 2Г |
|
|
|
|
|
|
|
|
|
| 5 | Р |
|
|
|
|
| 8 |
|
| Е |
|
|
|
|
| С |
|
| 9 |
| С |
|
|
|
|
|
|
|
|
|
| 4 |
|
|
|
|
|
| И |
|
|
|
|
|
|
| 3 |
|
|
|
|
|
|
|
|
|
| Я |
|
|
3. Контроль усвоения материала (письменный опрос).
Вариант I.
1) Определение возрастающей последовательности
Ответ: Последовательность  называется возрастающей, если каждый ее член, начиная со второго, больше предыдущего, т.е.
называется возрастающей, если каждый ее член, начиная со второго, больше предыдущего, т.е. 
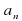 , где n
, где n 1.
1.
2) Последовательность  задана формулой
задана формулой 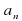 =
= . Найти
. Найти ;
;  ;
;  ;
;
Ответ: = 1;
= 1;  = 2,2;
= 2,2;  = 3,25.
= 3,25.
3) Последовательность задана формулой
задана формулой  = 3─2
= 3─2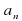 , где
, где = 2 и n
= 2 и n 1. Найти первые четыре члена последовательности.
1. Найти первые четыре члена последовательности.
Ответ: :  = 2;
= 2;  = ─1;
= ─1;  = 5;
= 5;  = ─7.
= ─7.
Вариант II.
1) Определение убывающей последовательности
Ответ: Последовательность  называется убывающей, если каждый ее член, начиная
называется убывающей, если каждый ее член, начиная
со второго, меньше предыдущего, т.е.  , где n
, где n 1.
1.
2) Последовательность задана формулой
задана формулой 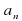 =
= . Найти
. Найти ;
;  ;
;  ;
;
Ответ:  =
=  ;
;  = ─ 0,6;
= ─ 0,6;  = ─1
= ─1 .
.
3) Последовательность задана формулой
задана формулой  = 3
= 3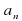 ─2, где
─2, где  = 2 и n
= 2 и n 1. Найти первые четыре члена последовательности.
1. Найти первые четыре члена последовательности.
Ответ: :  = 2;
= 2;  = 4;
= 4;  =10;
=10;  =28.
=28.
После сдачи работ провели предварительную проверку по готовым ответам.
4. Проверка заданий, работавших у доски.
В разгаданном кроссворде получили ключевое слово – прогрессия.
III. Изучение нового материала.
В данной главе нами будут рассмотрены две прогрессии: арифметическая и геометрическая.
Сначала рассмотрим арифметическую прогрессию.
1) Сообщение ученика: «Легенда о шахматной доске». ( Я.И.Перельман «Живая математика») - творческое задание.
Чтобы понять легенду, не нужно вовсе уметь играть в шахматы: достаточно знать, что игра происходит на доске, разграфленной на 64 клетки (попеременно черные и белые).
Шахматная игра была придумана в Индии, и когда индусский царь Шерам познакомился с нею, он был восхищен ее остроумием и разнообразием возможных в ней положений.
Узнав, что игра изобретена одним из его подданных, царь приказал его позвать, чтобы лично наградить за удачную выдумку. Изобретатель, его звали Сета, явился к трону повелителя. Это был скромно одетый ученый, получавший средства к жизни от своих учеников.
-- Я желаю достойно вознаградить тебя, Сета, за прекрасную игру, которую ты придумал, -- сказал царь. Мудрец поклонился.
-- Я достаточно богат, чтобы исполнить самое смелое твое пожелание, -- продолжал царь. –Назови награду, которая тебя удовлетворит, и ты получишь ее.
-- Велика доброта твоя, повелитель. Но дай срок обдумать ответ. Завтра, по зрелом размышлении, я сообщу тебе мою просьбу.
Когда на другой день Сета снова явился к ступеням трона, он удивил царя беспримерной скромностью своей просьбы.
--Повелитель, -- сказал Сета, -- прикажи выдать мне за первую клетку шахматной доски одно пшеничное зерно, за вторую —2 зерна, за третью — 4, за четвертую—8, за пятую – 16, за шестую –32…
-- Довольно, -- с раздражением прервал его царь, -- Ты получишь свои зерна за все 64 клетки доски, согласно твоему желанию: за каждую вдвое больше против предыдущей. Но знай, что просьба твоя недостойна моей щедрости. Ступай. Слуги мои вынесут тебе твой мешок с пшеницей. Сета улыбнулся, покинул залу и стал дожидаться у ворот дворца. За обедом царь поинтересовался, унес ли Сета свою жалкую награду. На что слуги ответили, что придворные математики исчисляют число следуемых зерен. Вечером отходя ко сну, царь еще раз осведомился, давно ли Сета ушел со своим мешком. Но узнал, что требуемое число зерен настолько велико, что во всех амбарах царя нет такого количества зерен. Не найдется такого числа зерен и на всем пространстве Земли.
Такова легенда.
2). Вернемся к шахматной доске. Речь в этой легенде идет о числе зерен, выданных за каждую клетку доски. Если все эти числа записать одно за другим, то получим последовательность чисел: 1; 2; 4; 8; …
Облегчим работу придворным математикам. Будем выдавать за каждую клетку доски число зерен на 2 больше, чем за предыдущую.
Получим последовательность (ребята помогают составлять последовательность)
1; 3; 5; 7; 9; 11;…
Эта последовательность называется арифметической прогрессией.
Что же такое арифметическая прогрессия?
Учащиеся пытаются сформулировать определение сами, а учитель задает им наводящие вопросы и корректирует ответы.
Учитель вместе с учащимися дает определение арифметической прогрессии, затем обращает ребят к определению в учебнике. Читают по учебнику еще раз.
Определение. Арифметической прогрессией называется последовательность, каждый член которой , начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом.
Запишем с помощью формулы данное определение.
Из определения следует:  =
= , где d–некоторое число.
, где d–некоторое число.
Выразим число d из данной формулы.
d =  ─
─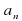 .
.
С помощью какого арифметического действия нашли число d ? (вычитания).
Значит, d─ разность арифметической прогрессии.
(Учитель читает стихотворение )
Разность прогрессии-
Это число.
Как же найти его?
Очень легко.
Нужно в прогрессии
Член последующий взять
И из него предыдущий отнять.
Ну и, конечно,
Потом посчитать.
IV. Решение примеров на доске (учитель показывает, как правильно оформлять решение в постоянном диалоге с учащимися).
Пример1.
Последовательность – арифметическая прогрессия, первые члены которой задаются числами: 2; 7; 12; 17; 22; 27…Найти разность арифметической прогрессии.
– арифметическая прогрессия, первые члены которой задаются числами: 2; 7; 12; 17; 22; 27…Найти разность арифметической прогрессии.
Оформление решения.
Дано: – арифметическая прогрессия
– арифметическая прогрессия
 : 2; 7; 12; 17; 22; 27…
: 2; 7; 12; 17; 22; 27…
Найти: d
Решение: d = ─
─ 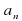
d = 7─2 = 5. Ответ: d = 5.
Как еще можно было вычислить число d?
(учащиеся дают ответы: 12─7; 17─12; 22─17; и т.д.)
Пример 2.
Найти первые пять членов арифметической прогрессии если
если  = 2 ,d = 3
= 2 ,d = 3
Оформление решения.
Дано: – арифметическая прогрессия
– арифметическая прогрессия
 = 2, d = 3
= 2, d = 3
Найти : ;
; ;
; ;
; .
.
Решение.
Из определения арифметической прогрессии  =
= 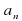 +d получаем:
+d получаем:
при n=1,  =
=  + d = 2 + 3 = 5 ;
+ d = 2 + 3 = 5 ;
при n=2,  =
=  + d = 5 + 3 = 8;
+ d = 5 + 3 = 8;
при n=3,  =
=  + d = 8 + 3 = 11;
+ d = 8 + 3 = 11;
при n=4,  =
= + d =11 + 3 = 14. Ответ: 2; 5; 8; 11; 14.
+ d =11 + 3 = 14. Ответ: 2; 5; 8; 11; 14.
(У доски работает ученик, а учитель только корректирует работу и призывает при необходимости к помощи класс. Учащиеся записывают в тетрадях.)
- Как называется формула, которой мы пользовались в этом задании? (рекуррентная).
- Что она позволяет найти? (она позволяет найти следующие члены последовательности, если известны один или несколько предыдущих членов).
V. Получим формулу n-го члена арифметической прогрессии.
(Учитель читает стихотворение)
Если разность прогрессии знать,
И знать число 
Можно прогрессии члены так
Один за другим получить.
Но долго так сидеть считать
Надо формулу лишь знать.
Все подставить , уточнить
И в ответе получить
Член прогрессии любой.
Если хочешь, 102-й.
(Учитель объясняет вывод формулы на доске в постоянном общении с классом. Ребята записывают в тетрадь.)
Из определения арифметической прогрессии  =
=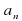 +d
+d
Как получить  =
=  + d
+ d
-  =
=  + d = (
+ d = ( + d )+d =
+ d )+d =  +2d
+2d
-  =
=  + d = (
+ d = ( + 2d )+d =
+ 2d )+d =  +3 d
+3 d
-  =
=  + d = (
+ d = ( + 3d )+d =
+ 3d )+d =  +4 d
+4 d
По аналогии получим 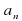
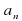 =
=  + d(n ─ 1)
+ d(n ─ 1)
Таким образом получена важнейшая формула - формула n-го члена арифметической прогрессии.
VI. Применение формулы n-го члена арифметической прогрессии.
Пример 3.
Последовательность ( )─ арифметическая прогрессия. Найдите
)─ арифметическая прогрессия. Найдите ;
; ;
; , если
, если  = 20, d = 3
= 20, d = 3
Оформление решения.
Дано: ( ) – арифметическая прогрессия
) – арифметическая прогрессия
 = 20, d = 3
= 20, d = 3
Найти : ;
; ;
; ,
,
Решение.
Используем формулу n-го члена арифметической прогрессии.
 =
=  +7d,
+7d,  = 20 +7∙3 = 41
= 20 +7∙3 = 41
 =
=  +10d,
+10d,  = 20+10∙3 = 50
= 20+10∙3 = 50
 =
=  +41d,
+41d,  = 20+41∙3= 143 Ответ:
= 20+41∙3= 143 Ответ:  =41,
=41,  =50,
=50,  =143.
=143.
(Один ученик пишет на доске, остальные в тетрадях.)
VII. Закрепление изученного материала.
(Учащиеся разбиты на группы. В каждой группе есть ученик –консультант, который помогает остальным членам группы)
№575(а,в)
– Какие элементы даны? ( и d )
и d )
- Как найти ? (к
? (к  прибавить d )
прибавить d )
- Как найти  ? (к
? (к прибавить d )
прибавить d )
Выполните задание ( смотреть разобранный пример 1)
Решение.
а)  =
=  + d = 10 + 4 = 14
+ d = 10 + 4 = 14
 =
=  + d = 14 + 4 = 18
+ d = 14 + 4 = 18
 =
=  + d = 18 + 4 = 22
+ d = 18 + 4 = 22
 =
=  + d = 22 + 4 = 26 Ответ:
+ d = 22 + 4 = 26 Ответ:  = 10,
= 10,  = 14,
= 14,  = 18,
= 18,  = 22,
= 22,  = 26.
= 26.
в)  =
=  + d = 1,7+(─0,2) =1,5
+ d = 1,7+(─0,2) =1,5
 =
=  + d = 1,5 +(─0,2) = 1,3
+ d = 1,5 +(─0,2) = 1,3
 =
=  + d = 1,3 +(─0,2) = 1,1
+ d = 1,3 +(─0,2) = 1,1
 =
=  + d =1,1 +(─0,2) = 0,9 Ответ:
+ d =1,1 +(─0,2) = 0,9 Ответ:  = 1,7,
= 1,7,  = 1,5,
= 1,5,  = 1,3,
= 1,3,  = 1,1,
= 1,1,  = 0,9
= 0,9
Провели проверку.
№576(а,в,д)
- Какой формулой нужно воспользоваться? (Формулой n-го члена арифметической прогрессии). Запишите формулу. Выразите а) , в)
, в) , д)
, д) 
Решение.
а)  =
=  +6d, в)
+6d, в)  =
=  +230d, д)
+230d, д)  =
=  + d(к+5─1)=
+ d(к+5─1)=  +d(к+4)
+d(к+4)
Провели проверку.
№577(б)
Решение.
 =
=  +20d,
+20d,  =5,8 +20 ∙ (─1,5) = 5,8 ─30 = ─24,2.
=5,8 +20 ∙ (─1,5) = 5,8 ─30 = ─24,2.
Ответ:  =─24,2.
=─24,2.
№580(а)
Чтобы найти n-й член арифметической прогрессии, что нужно знать? ( и d). Где взять
и d). Где взять ?
?
( Он на первом месте в записи прогрессии). Чему он равен? ( = ─8). А есть ли у вас d? (Нет, но можно найти). Как найти d? (из последующего члена прогрессии вычесть предыдущий, т.е. из
= ─8). А есть ли у вас d? (Нет, но можно найти). Как найти d? (из последующего члена прогрессии вычесть предыдущий, т.е. из  вычесть
вычесть ). Найдите d.
). Найдите d.
 = ─8,
= ─8,  = ─ 6,5, тогда d =
= ─ 6,5, тогда d =  ─
─  = ─ 6,5 – (─8) = 1,5
= ─ 6,5 – (─8) = 1,5
Найдите  и
и 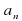
1)  =
=  +22d,
+22d,  = ─8 + 22 ∙ 1,5 = ─8 + 33 = 25
= ─8 + 22 ∙ 1,5 = ─8 + 33 = 25
2) 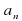 =
=  + d(n ─ 1),
+ d(n ─ 1), 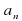 = ─ 8+1,5(n ─ 1) = ─ 8 +1,5n ─1,5 =─9,5 +1,5n
= ─ 8+1,5(n ─ 1) = ─ 8 +1,5n ─1,5 =─9,5 +1,5n
Ответ:  = 25,
= 25, 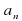 = ─9,5+1,5n
= ─9,5+1,5n
№584(б).
Если дан 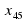 , можно ли его выразить с помощью формулы? (да, можно).
, можно ли его выразить с помощью формулы? (да, можно). 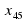 =
=  + 44d
+ 44d
Подставьте в формулу все данные. ─208 =  + 44∙(─7).Что получили? (уравнение). Решите его и найдите
+ 44∙(─7).Что получили? (уравнение). Решите его и найдите . Ответ
. Ответ  =100.
=100.
VIII. Контрольные вопросы:
1) С какой последовательностью мы познакомились на уроке?
2) Что такое d и как его найти?
3) Назовите формулу n -го члена.
4) Что нужно знать, чтобы найти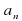 ?
?
IX. Домашнее задание.
1) Теория. §9 п.25
2) №575(б,г), №576(б,г,е), №578(а), №580(б), №584(а).
X. Подведение итогов урока.
Тему с вами разобрали
И задачки порешали
Подошел к концу урок
Подводить пора итог.
Литература:
1. Учебник Алгебра 9 класс Ю.Н.Макарычев и др. М.Просвещение 2014.
2. Поурочные разработки по алгебре 9 класс к учебнику Ю.Н.Макарычева А.Н.Рурукин, С.А.Полякова М. «ВАКО»,2015.
3. «Живая математика» И.Я.Перельман М, издательство «Наука» 1970.







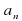 ) следует за:
) следует за: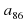 ;
; 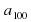 ;
; 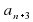 ;
;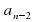 ;
; 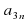
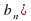 предшествует:
предшествует: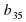 ;
; 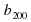 ;
; 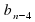 ;
; 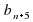 ;
; 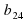
 ), расположенные между:
), расположенные между: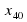 и
и 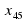 б)
б) 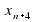 в)
в) 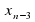 и
и 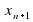
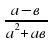 ─
─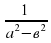 ∙
∙ 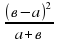 ) :
) : 









