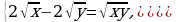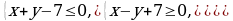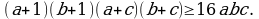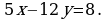Критерии и нормы оценки знаний, умений и навыков обучающихся. 1. Оценка письменных контрольных работ обучающихся.
Ответ оценивается отметкой «5», если:
работа выполнена полностью;
в логических рассуждениях и обосновании решения нет пробелов и ошибок;
в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).
Отметка «4» ставится в следующих случаях:
работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).
Отметка «3» ставится, если:
допущено более одной ошибки или более двух – трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.
Отметка «2» ставится, если:
допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.
Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.
2. Оценка устных ответов обучающихся.
Ответ оценивается отметкой «5», если ученик:
полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;
изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;
правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;
продемонстрировал знание теории ранее изученных сопутствующих тем, сформированность и устойчивость используемых при ответе умений и навыков;
отвечал самостоятельно, без наводящих вопросов учителя;
возможны одна – две неточности при освещении второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.
Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:
в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;
допущены один – два недочета при освещении основного содержания ответа, исправленные после замечания учителя;
допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.
Отметка «3» ставится в следующих случаях:
неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала;
имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.
Отметка «2» ставится в следующих случаях:
не раскрыто основное содержание учебного материала;
обнаружено незнание учеником большей или наиболее важной части учебного материала;
допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.
3 Грубыми считаются ошибки:
незнание определения основных понятий, законов, правил, основных положений теории, незнание формул, общепринятых символов обозначений величин, единиц их измерения;
незнание наименований единиц измерения;
неумение выделить в ответе главное;
неумение применять знания, алгоритмы для решения задач;
неумение делать выводы и обобщения;
неумение читать и строить графики;
неумение пользоваться первоисточниками, учебником и справочниками;
потеря корня или сохранение постороннего корня;
отбрасывание без объяснений одного из них;
равнозначные им ошибки;
вычислительные ошибки, если они не являются опиской;
логические ошибки.
3.2. К негрубым ошибкам следует отнести:
неточность формулировок, определений, понятий, теорий, вызванная неполнотой охвата основных признаков определяемого понятия или заменой одного - двух из этих признаков второстепенными;
неточность графика;
нерациональный метод решения задачи или недостаточно продуманный план ответа (нарушение логики, подмена отдельных основных вопросов второстепенными);
нерациональные методы работы со справочной и другой литературой;
неумение решать задачи, выполнять задания в общем виде.
3.3. Недочетами являются:
- небрежное выполнение записей, чертежей, схем, графиков
Контрольные работы по алгебре
Контрольная работа №1 (1 час)
Вариант 1
Дан многочлен 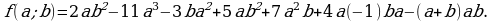
а) Приведите данный многочлен к стандартному виду.
б) Установите, является ли данный многочлен однородным.
в) Если многочлен является однородным, то определите его степень.
Разложите многочлен на множители:
а) 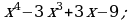 б)
б) 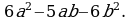
Решите уравнение: 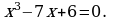
Докажите, что выражение 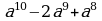 делится на
делится на 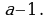
При каких значениях параметров 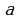 и
и 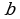 многочлен
многочлен 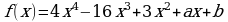 делится без остатка на многочлен
делится без остатка на многочлен 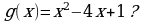
Контрольная работа №1 (1 час)
Вариант 2
Дан многочлен 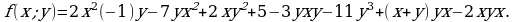
а) Приведите данный многочлен к стандартному виду.
б) Установите, является ли данный многочлен однородным.
в) Если многочлен является однородным, то определите его степень.
Разложите многочлен на множители:
а) 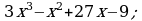 б)
б) 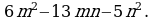
Решите уравнение: 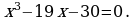
Докажите, что выражение 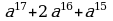 делится на
делится на 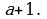
При каких значениях параметров 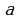 и
и 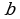 многочлен
многочлен 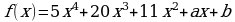 делится без остатка на многочлен
делится без остатка на многочлен 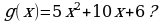
Контрольная работа №2 (2 часа)
Вариант 1
Вычислите: а) 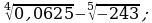 б)
б) 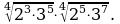
Решите уравнение: а) 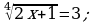 б)
б) 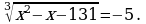
Постройте график функции: 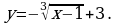
Найдите область определения функции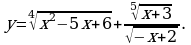
Упростите выражение 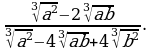
Расположите в порядке убывания следующие числа: 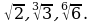
Упростите выражение 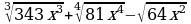 , найдите его значение при
, найдите его значение при 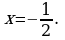
Решите неравенство 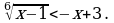
Решите уравнение: 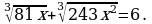
Контрольная работа №2 (2 часа)
Вариант 2
Вычислите: а) 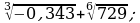 б)
б) 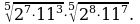
Решите уравнение: а) 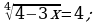 б)
б) 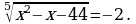
Постройте график функции: 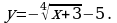
Найдите область определения функции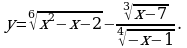
Упростите выражение 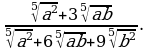
Расположите в порядке убывания следующие числа: 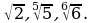
Упростите выражение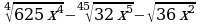 ,найдите его значение при
,найдите его значение при 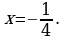
Решите неравенство 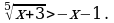
Решите уравнение: 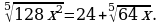
Контрольная работа №3 (1 час)
Вариант 1
Вычислите: а) 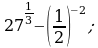 б)
б) 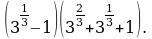
Упростите выражение: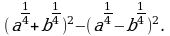
Решите уравнение: 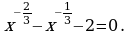
Составьте уравнение касательной к графику функции 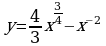 в точке х=1.
в точке х=1.
Решите неравенство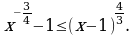
Решите уравнение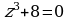 на множестве комплексных чисел.
на множестве комплексных чисел.
Контрольная работа №3 (1 час)
Вариант 2
Вычислите: а) 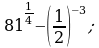 б)
б) 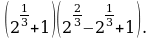
Упростите выражение: 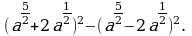
Решите уравнение: 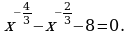
Составьте уравнение касательной к графику функции 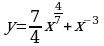 в точке х=1.
в точке х=1.
Решите неравенство 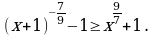
Решите уравнение 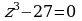 на множестве комплексных чисел.
на множестве комплексных чисел.
Контрольная работа №4 (2 часа)
Вариант 1
Постройте график функции: а) 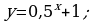 б)
б) 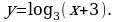
Решите уравнение: а) 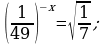 б)
б) 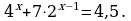
Решите неравенство: 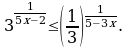
Вычислите: 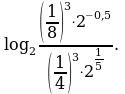
Сравните числа a и b, если: а) 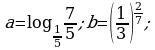 б)
б) 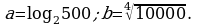
Решите неравенство: 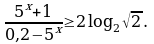
Решите неравенство: 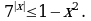
Контрольная работа №4 (2 часа)
Вариант 2
Постройте график функции: а) 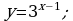 б)
б) 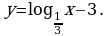
Решите уравнение: а) 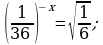 б)
б) 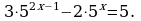
Решите неравенство: 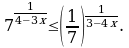
Вычислите: 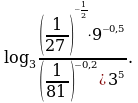
Сравните числа a и b, если: а) 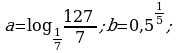 б)
б) 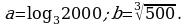
Решите неравенство: 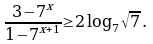
Решите неравенство: 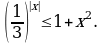
Контрольная работа № 5 (2 часа)
Вариант 1
Вычислите 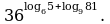
Решите уравнение: а) 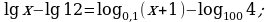
б) 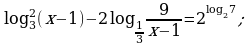
в) 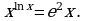
Решите неравенство: а) 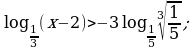 б)
б) 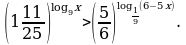
Исследуйте функцию 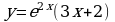 на монотонность и экстремумы.
на монотонность и экстремумы.
К графику функции 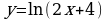 проведена касательная, параллельная прямой
проведена касательная, параллельная прямой 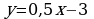 . Найдите точку пересечения этой касательной с осью х.
. Найдите точку пересечения этой касательной с осью х.
Решите неравенство: 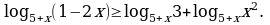
Решите систему уравнений 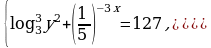
Контрольная работа № 5 (2 часа)
Вариант 2
Вычислите 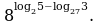
Решите уравнение: а) 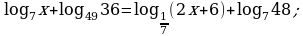
б) 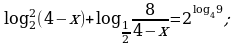
в) 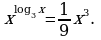
Решите неравенство: а) 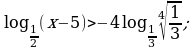 б)
б) 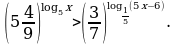
Исследуйте функцию 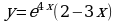 на монотонность и экстремумы.
на монотонность и экстремумы.
К графику функции 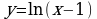 проведена касательная, параллельная биссектрисе первой координатной четверти. Найдите площадь треугольника, образованного этой касательной и осями координат.
проведена касательная, параллельная биссектрисе первой координатной четверти. Найдите площадь треугольника, образованного этой касательной и осями координат.
Решите неравенство: 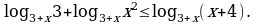
Решите систему уравнений 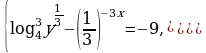
Контрольная работа №6 (1 час)
Вариант 1
Докажите, что функция 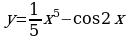 является первообразной для функции
является первообразной для функции 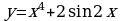 .
.
Для функции 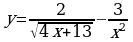 найдите ту первообразную, график которой проходит через заданную А (-3;-2).
найдите ту первообразную, график которой проходит через заданную А (-3;-2).
Вычислите определённый интеграл: а) 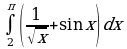 ; б)
; б) 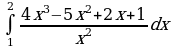 .
.
Найдите площадь фигуры, ограниченной линиями 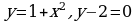 .
.
Известно, что функция 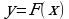 – первообразная для функции
– первообразная для функции 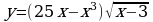 . Исследуйте функцию
. Исследуйте функцию 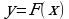 на монотонность и экстремумы.
на монотонность и экстремумы.
При каких значениях параметра а выполняется неравенство 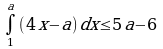 ?
?
Контрольная работа №6 (1 час)
Вариант 2
Докажите, что функция 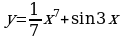 является первообразной для функции
является первообразной для функции 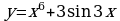 .
.
Для функции 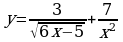 найдите ту первообразную, график которой проходит через заданную А (1;-5).
найдите ту первообразную, график которой проходит через заданную А (1;-5).
Вычислите определённый интеграл: а) 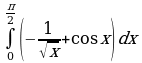 ; б)
; б) 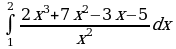 .
.
Найдите площадь фигуры, ограниченной линиями 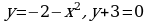 .
.
Известно, что функция 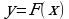 – первообразная для функции
– первообразная для функции 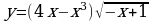 . Исследуйте функцию
. Исследуйте функцию 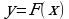 на монотонность и экстремумы.
на монотонность и экстремумы.
При каких значениях параметра b выполняется неравенство 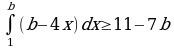 ?
?
Контрольная работа №7 (2 часа)
Вариант 1
Решите уравнение: а) 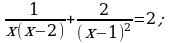
б) 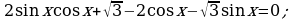
в) 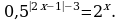
Решите неравенство: а) 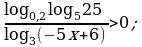 б)
б) 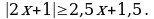
Решите уравнение 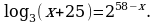
Решите уравнение 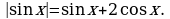
Внутри равнобедренного прямоугольного треугольника случайным образом выбрана точка. Какова вероятность того, что она расположена ближе к вершине прямого угла, чем к вершинам острых углов треугольника?
Решите уравнение: 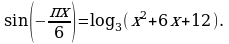
Контрольная работа №7 (2 часа)
Вариант 2
Решите уравнение: а) 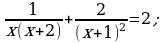
б) 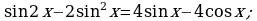
в) 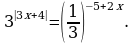
Решите неравенство: а) 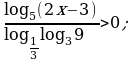 б)
б) 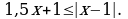
Решите уравнение 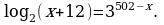
Решите уравнение 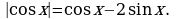
Внутри квадрата случайным образом выбрана точка. Какова вероятность того, что она расположена внутри вписанного в него круга?
Решите уравнение: 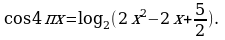
Контрольная работа №8 (2 часа)
Вариант 1
Решите уравнение: а) 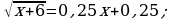 б)
б) 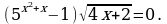
Решите неравенство: а) 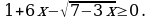
Решите систему уравнений: а)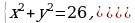 б)
б) 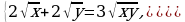
Найдите площадь фигуры, заданной системой неравенств 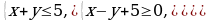
Докажите, что для любых неотрицательных чисел a и b выполняется неравенство 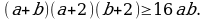
Решите уравнение в целых числах 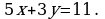
Три данных числа образуют арифметическую прогрессию. Если третий член прогрессии уменьшить на 3, то полученные три числа составят геометрическую прогрессию. Если второй член этой геометрической прогрессии уменьшить на 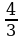 , то полученные три числа вновь составят геометрическую прогрессию. Найдите данные числа.
, то полученные три числа вновь составят геометрическую прогрессию. Найдите данные числа.
Контрольная работа №8 (2 часа)
Вариант 2
Решите уравнение: а) 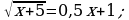 б)
б) 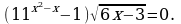
Решите неравенство: а) 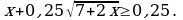
Решите систему уравнений: а)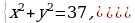 б)
б) 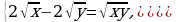
Найдите площадь фигуры, заданной системой неравенств 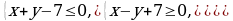
Докажите, что для любых неотрицательных чисел a, b и с выполняется неравенство 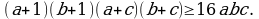
Решите уравнение в целых числах 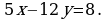
Три данных числа образуют геометрическую прогрессию. Если второй член прогрессии увеличить на 2, то полученные числа составят арифметическую прогрессию. Если третий член новой прогрессии увеличить на 9, то полученные три числа составят геометрическую прогрессию. Найдите данные числа.
Контрольные работы по геометрии
Контрольная работа № 5.1
Вариант 1
1. Вычислите скалярное произведение векторов 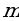 и
и 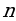 , если
, если 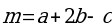 ,
, 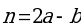 ,
, 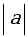 = 2,
= 2, 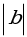 = 3,
= 3, 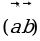 = 60°,
= 60°, 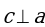 ,
, 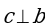 .
.
2. Дан куб ABCDA1B1C1D1. Найдите угол между прямыми AD1 и BM, где M – середина ребра DD1.
3. При движении прямая а отображается на прямую а1, а плоскость α – на плоскость α1. Докажите, что если и а || α, то а₁||α₁.
Контрольная работа № 5.1
Вариант 2
1. Вычислите скалярное произведение векторов 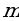 и
и 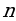 , если
, если 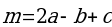 ,
, 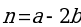 ,
, 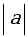 = 3,
= 3, 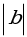 = 2,
= 2, 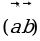 = 60°,
= 60°, 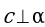 ,
, 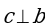 .
.
2. Дан куб ABCDA1B1C1D1. Найдите угол между прямыми AC и DC1.
При движении прямая a отображается на прямую a1, плоскость α – на плоскость α1, . Докажите, что если 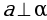 , то
, то 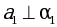 .
.
Контрольная работа № 6.1
Вариант 1
1. Осевое сечение цилиндра – квадрат, площадь основания цилиндра равна 16π см2. Найдите площадь поверхности цилиндра.
2. Высота конуса равна 6 см, угол при вершине осевого сечения равен 120°. Найдите:
а) площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми 30°;
б) площадь боковой поверхности конуса.
3. Диаметр шара равен 2m. Через конец диаметра проведена плоскость под углом 45° к нему. Найдите длину линии пересечения сферы с этой плоскостью.
Контрольная работа № 6.1
Вариант 2
1. Осевое сечение цилиндра – квадрат, диагональ которого 4 см. Найдите площадь поверхности цилиндра.
2. Радиус основания конуса равен 6 см, а образующая наклонена к плоскости основания под углом 30°. Найдите:
а) площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми 60°;
б) площадь боковой поверхности конуса.
3. Диаметр шара равен 4m. Через конец диаметра проведена плоскость под углом 30° к нему. Найдите площадь сечения шара этой плоскостью.
Контрольная работа № 7.1
Вариант 1
1. Диаметр шара равен высоте конуса, образующая которого составляет с плоскостью основания угол в 60°. Найдите отношение объемов конуса и шара.
2. Объем цилиндра равен 96π см3, площадь его осевого сечения 48 см2. Найдите площадь сферы, описанной около цилиндра.
Контрольная работа № 7.1
Вариант 2
1. В конус, осевое сечение которого есть правильный треугольник, вписан шар. Найдите отношение площади сферы к площади боковой поверхности конуса.
2. Диаметр шара равен высоте цилиндра, осевое сечение которого есть квадрат. Найдите отношение объемов цилиндра и шара.







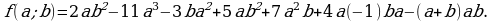
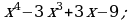 б)
б) 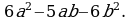
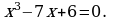
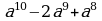 делится на
делится на 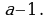
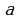 и
и 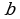 многочлен
многочлен 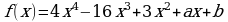 делится без остатка на многочлен
делится без остатка на многочлен 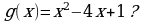
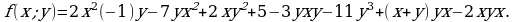
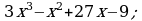 б)
б) 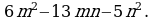
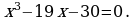
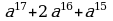 делится на
делится на 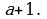
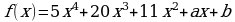 делится без остатка на многочлен
делится без остатка на многочлен 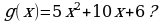
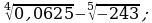 б)
б) 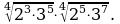
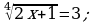 б)
б) 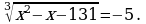
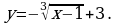
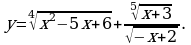
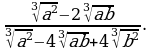
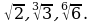
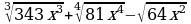 , найдите его значение при
, найдите его значение при 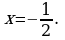
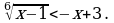
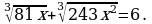
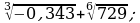 б)
б) 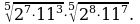
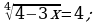 б)
б) 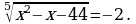
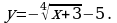
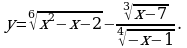
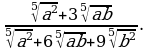
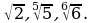
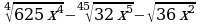 ,найдите его значение при
,найдите его значение при 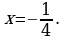
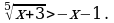
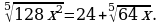
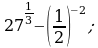 б)
б) 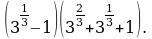
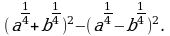
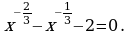
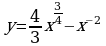 в точке х=1.
в точке х=1.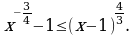
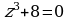 на множестве комплексных чисел.
на множестве комплексных чисел.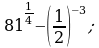 б)
б) 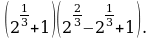
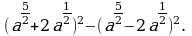
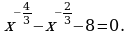
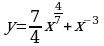 в точке х=1.
в точке х=1.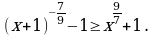
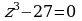 на множестве комплексных чисел.
на множестве комплексных чисел.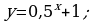 б)
б) 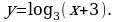
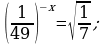 б)
б) 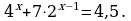
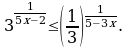
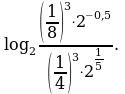
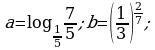 б)
б) 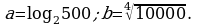
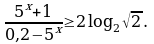
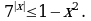
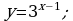 б)
б) 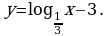
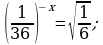 б)
б) 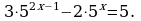
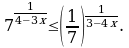
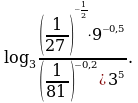
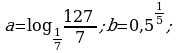 б)
б) 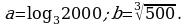
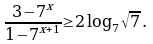
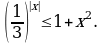
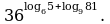
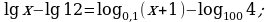
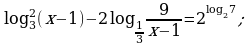
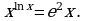
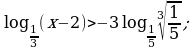 б)
б) 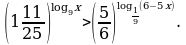
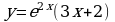 на монотонность и экстремумы.
на монотонность и экстремумы.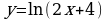 проведена касательная, параллельная прямой
проведена касательная, параллельная прямой 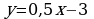 . Найдите точку пересечения этой касательной с осью х.
. Найдите точку пересечения этой касательной с осью х.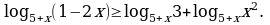
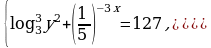
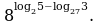
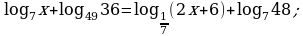
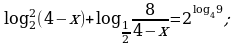
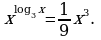
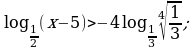 б)
б) 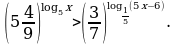
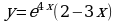 на монотонность и экстремумы.
на монотонность и экстремумы.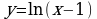 проведена касательная, параллельная биссектрисе первой координатной четверти. Найдите площадь треугольника, образованного этой касательной и осями координат.
проведена касательная, параллельная биссектрисе первой координатной четверти. Найдите площадь треугольника, образованного этой касательной и осями координат.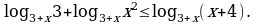
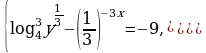
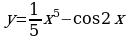 является первообразной для функции
является первообразной для функции 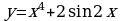 .
.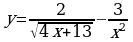 найдите ту первообразную, график которой проходит через заданную А (-3;-2).
найдите ту первообразную, график которой проходит через заданную А (-3;-2).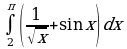 ; б)
; б) 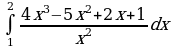 .
.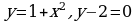 .
.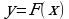 – первообразная для функции
– первообразная для функции 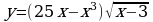 . Исследуйте функцию
. Исследуйте функцию 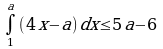 ?
?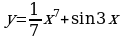 является первообразной для функции
является первообразной для функции 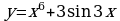 .
.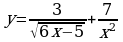 найдите ту первообразную, график которой проходит через заданную А (1;-5).
найдите ту первообразную, график которой проходит через заданную А (1;-5).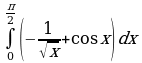 ; б)
; б) 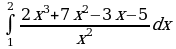 .
.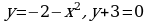 .
.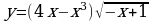 . Исследуйте функцию
. Исследуйте функцию 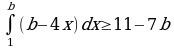 ?
?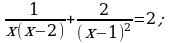
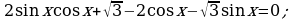
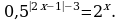
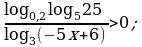 б)
б) 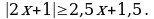
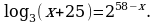
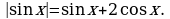
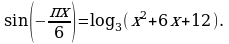
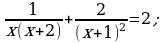
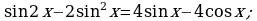
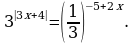
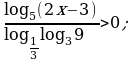 б)
б) 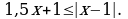
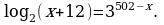
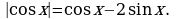
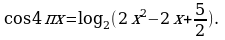
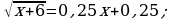 б)
б) 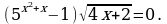
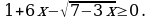
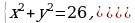 б)
б) 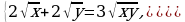
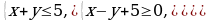
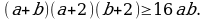
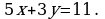
 , то полученные три числа вновь составят геометрическую прогрессию. Найдите данные числа.
, то полученные три числа вновь составят геометрическую прогрессию. Найдите данные числа. б)
б) 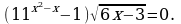
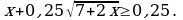
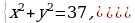 б)
б)