Если радиус и высота конуса соответственно равны 2см и 3/π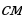 , то объем конуса равен…
, то объем конуса равен…
Если радиус шара равен 3см, то его объем равен…
Если шар радиуса r вписан в цилиндр, то площадь боковой поверхности цилиндра равна…
Если в конус, высота и радиус основания которого соответственно равны 3см и 4см, вписана правильная треугольная пирамида, то ее боковое ребро равно…
В основании прямой призмы лежит равнобедренный треугольник с боковой стороной 17см и высотой, проведенной к основанию, равной 15см. Диагональ боковой грани, содержащей основание треугольника, образует с плоскостью основания угол 30®. Найти объем призмы.
В основании цилиндра проведена хорда, стягивающая дугу 60°. Отрезок, соединяющий центр другого основания с серединой этой хорды, равен 6 см и образует с плоскостью основания угол 45°. Найти объем цилиндра
Из центра основания конуса к образующей проведен перпендикуляр, составляющий с высотой угол β. Образующая конуса равна с. Найти объем конуса.
Если радиус и высота цилиндра соответственно равны 2см и 3/π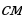 , то объем цилиндра равен…
, то объем цилиндра равен…
Если объем шара равен 36π см3, то его радиус равен…
Если шар радиуса r вписан в цилиндр, то объем цилиндра равен…
Если в правильную четырехугольную пирамиду, высота и сторона основания которой равны 4 и
В основании прямой призмы лежит ромб с диагоналями 12см и 16см. Диагональ боковой грани образует с плоскостью основания угол 45®. Найти объем призмы.
В основании цилиндра проведена хорда, которую видно из центра основания под углом 120°. Отрезок, соединяющий центр одного основания с точкой окружности другого основания, образует с плоскостью основания угол 45°. Расстояние от центра до хорды равно 3см. Найти объем цилиндра.
Хорда основания конуса равна а и стягивает дугу α. Отрезок, соединяющий вершину конуса с серединой хорды, наклонен к основанию под углом β. Найти объем конуса.







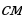 , то объем конуса равен…
, то объем конуса равен…









