Презентация к уроку геометрии 8 класс " Теорема Пифагора"

ТЕОРЕМА ПИФАГОРА

Урок геометрии в 8 классе

учитель математики: Громова Н. В.

МБОУ « Ужурская СОШ№1 им. А. К. Харченко»

2013-2014 уч.год

Содержание:

1). Организационный момент

2). Актуализация знаний

3). Историческая справка

4). Теорема Пифагора

5). Первичное закрепление теоремы

6). Старинная задача

7). Итог урока

ВОПРОСЫ:

1. Какой четырехугольник называется квадратом ?

2. Как найти площадь квадрата?

3. Какой треугольник называют прямоугольным?

4. Как называются стороны прямоугольного треугольника?

5. Как найти площадь прямоугольного треугольника?

18

ЗАДАЧА №1 НАЙДИТЕ ПЛОЩАДЬ ТРЕУГОЛЬНИКА АВС, ЕСЛИ ∠ А=60°, АВ = 18 СМ, ВС = 6 СМ.

А

60°

В

С

6

Ответ: 27

18

ЗАДАЧА №2 НАЙДИТЕ ПЛОЩАДЬ ТРЕУГОЛЬНИКА АВС, ЕСЛИ АВ = 13 СМ, ВС = 5 СМ.

А

В

С

6

?

Пифагор Самосский (ок. 580 — ок. 500 до н. э.) — древнегреческий философ, религиозный и политический деятель, основатель пифагореизма, математик. Пифагору приписывается изучение свойств целых чисел и пропорций, доказательство теоремы Пифагора и др.

Школа Пифагора, или, как ее еще называют, пифагорейский союз, была одновременно и философской школой, и политической партией, и религиозным братством.

Рафаэль. Пифагор в окружении учеников.

Предание гласит, что когда Пифагор пришёл к теореме, носящей его имя, он принёс богам 100 быков. В пятисотых годах до нашей эры Пифагор был убит в уличной схватке во время народного восстания.

В настоящее время известно около 200 доказательств теоремы Пифагора.

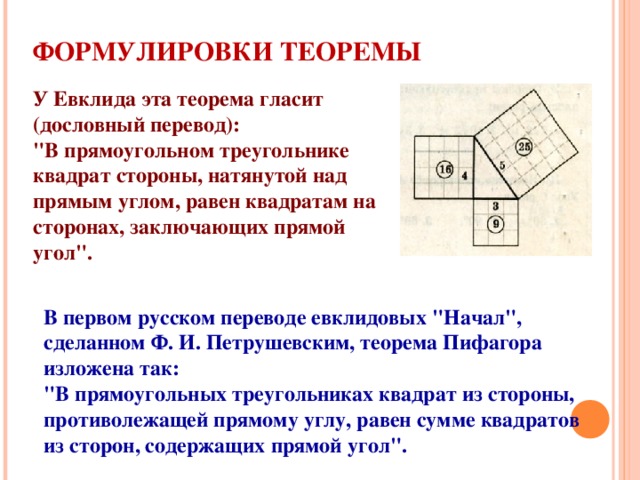
ФОРМУЛИРОВКИ ТЕОРЕМЫ

У Евклида эта теорема гласит (дословный перевод):

"В прямоугольном треугольнике квадрат стороны, натянутой над прямым углом, равен квадратам на сторонах, заключающих прямой угол".

В первом русском переводе евклидовых "Начал", сделанном Ф. И. Петрушевским, теорема Пифагора изложена так:

"В прямоугольных треугольниках квадрат из стороны, противолежащей прямому углу, равен сумме квадратов из сторон, содержащих прямой угол".

В прямоугольном треугольнике квадрат

гипотенузы равен сумме квадратов катетов

Дано: прямоугольный треугольник

а, в – катеты, с – гипотенуза

Доказать:

c

а

Доказательство:

b

- площадь квадрата

- теорема доказана .

Вариант 1

№ 483(а)

Вариант 2

№ 484(а)

10

5

С ПОМОЩЬЮ ТЕОРЕМЫ ПИФАГОРА МОЖНО РЕШАТЬ ДВА ВИДА ЗАДАЧ:

1. Найти гипотенузу прямоугольного треугольника, если известны катеты .

.

2. Найти катет, если известна гипотенуза и другой катет.

Старинная задача

Случися некоему человеку к стене

лестницу прибрати, стены тоя же

высота есть 117 стоп. И обрете лестницу

долютою 125 стоп.

И ведати хочет, колико стоп сея лестницы

нижней конец от стены отстояти имать .

125

117

?

«Делай лишь то, что впоследствии не огорчит тебя и не принудит раскаиваться.»

цитата Пифагора

Пифагор Самосский (римская копия)

ИТОГ УРОКА

Что нового вы узнали сегодня на уроке?

Для каких треугольников применяется теорема Пифагора?

В чём заключается теорема Пифагора?

ДОМАШНЕЕ ЗАДАНИЕ:

П. 54, № 487

Исследовательская работа:

найти в интернете другие доказательства теоремы

Литература :

• Л. С. Атанасян , «Геометрия 7-9» М,: Просвещение, 2009г.
• Энциклопедический словарь юного математика
• http://ru/wikipedia.org/wik
• http://festival.1september.ru/articles
• http://moyoifahor.narod.ruluse.htm