Пояснительная записка
Рабочая программа по математике составлена на основе федерального компонента государственного стандарта основного общего образования.
Данная рабочая программа ориентирована на учащихся 8 класса и реализуется на основе следующих документов:
Примерные программы по учебным предметам. Математика. 5—9 классы: проект. — 3-е изд., перераб. М.: Просвещение, 2011. 64 с. — (Стандарты второго поколения).
Общая характеристика учебного предмета.
Математическое образование является обязательной и неотъемлемой частью общего образования на всех ступенях школы. Обучение математике в основной школе направлено на достижение следующих целей:
1) в направлении личностного развития:
формирование представлений о математике как части общечеловеческой культуры, о значимости математики в развитии цивилизации и современного общества;
развитие логического и критического мышления, культуры речи, способности к умственному эксперименту;
формирование интеллектуальной честности и объективности, способности к преодолению мыслительных стереотипов, вытекающих из обыденного опыта;
воспитание качеств личности, обеспечивающих социальную мобильность, способность принимать самостоятельные решения;
формирование качеств мышления, необходимых для адаптации в современном информационном обществе;
. • развитие интереса к математическому творчеству и математических способностей;
в метапредметном направлении:
развитие представлений о математике как форме описания и методе познания действительности, создание условий для приобретения первоначального опыта математического моделирования;
формирование общих способов интеллектуальной деятельности характерных для математики и являющихся основой познавательной культуры, значимой для различных сфер человеческой деятельности;
в предметном направлении:
овладение математическими знаниями и умениями, необходимыми для продолжения образования, изучения смежных дисциплин, применения в повседневной жизни,
создание фундамента для математического развития, формирования механизмов мышления, характерных для математической деятельности.
Описание места учебного предмета в учебном плане
Базисный учебный (образовательный) план на изучение математики в основной школе отводит
5 учебных часов в неделю. Учебное время увеличено до 6 уроков в неделю за счет часов школьного компонента, всего 210 уроков.
Согласно проекту Базисного учебного (образовательного) плана, в 8 классе изучаются предметы «Алгебра» и «Геометрия».
Описание ценностных ориентиров содержания учебного предмета
Математическое образование играет важную роль как в практической, так и в духовной жизни общества. Практическая сторона математического образования связана с формированием способов деятельности, духовная — с интеллектуальным развитием человека, формированием характера и общей культуры.
Практическая полезность математики обусловлена тем, что ее предметом являются фундаментальные структуры реального мира: пространственные формы и количественные отношения — от простейших, усваиваемых в непосредственном опыте, до достаточно сложных, необходимых для развития научных и технологических идей. Без конкретных математических знаний затруднено понимание принципов устройства и использования современной техники, восприятие и интерпретация разнообразной социальной, экономической, политической информации, малоэффективна повседневная практическая деятельность. Каждому человеку в своей жизни приходится выполнять достаточно сложные расчеты, находить в справочниках нужные формулы и применять их, владеть практическими приемами геометрических измерений и построений, читать информацию, представленную в виду таблиц, диаграмм, графиков, понимать вероятностный характер случайных событий, составлять несложные алгоритмы и др.
Без базовой математической подготовки невозможно стать образованным современным человеком. В школе математика служит опорным предметом для изучения смежных дисциплин. В послешкольной жизни реальной необходимостью в наши дни является непрерывное образование, что требует полноценной базовой общеобразовательной подготовки, в том числе и математической. И наконец, все больше специальностей, где необходим высокий уровень образования, связано с непосредственным применением математики (экономика, бизнес, финансы, физика, химия, техника, информатика, биология, психология и др.). Таким образом, расширяется круг школьников, для которых математика становится значимым предметом.
Для жизни в современном обществе важным является формирование математического стиля мышления, проявляющегося в определенных умственных навыках. В процессе математическом деятельности в арсенал приемов и методов человеческого мышления естественным образом включаются индукция и дедукция, обобщение и конкретизация, анализ и синтез, классификация и систематизация, абстрагирование и аналогия. Объекты математических умозаключений и правила их конструирования вскрывают механизм логических построений, вырабатывают умения формулировать, обосновывать и доказывать суждения, тем самым развивают логическое мышление. Ведущая роль принадлежит математике в формировании алгоритмического мышления и воспитании умений действовать по заданному алгоритму и конструировать новые. В ходе решения задач — основной учебной деятельности на уроках математики — развиваются творческая и прикладная стороны мышления.
Обучение математике дает возможность развивать у учащихся точную, экономную и информативную речь, умение отбирать наиболее подходящие языковые (в частности, символические, графические) средства.
Математическое образование вносит свой вклад в формирование общей культуры человека. Необходимым компонентом общей культуры в современном толковании является общее знакомство с методами познания действительности, представление о предмете и методе математики, его отличия от методов естественных и гуманитарных наук, об особенностях применения математики для решения научных и прикладных задач.
Изучение математики способствует эстетическому воспитанию человека, пониманию красоты и изящества математических рассуждений, восприятию геометрических форм, усвоению идеи симметрии.
История развития математического знания дает возможность пополнить запас историко-научных знаний школьников, сформировать у них представления о математике как части общечеловеческой культуры. Знакомство с основными историческими вехами возникновения и развития математической науки, с историей великих открытий, именами людей, творивших науку, должно войти в интеллектуальный багаж каждого культурного человека.
Содержание учебного предмета
1. Рациональные дроби (25 ч).
Рациональная дробь. Основное свойство дроби, сокращение дробей. Тождественные преобразования рациональных выражений. Функция 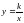 и ее график.
и ее график.
Основная цель: выработать умение выполнять тождественные преобразования рациональных выражений.
Главное место в данной теме занимают алгоритмы действий с дробями. Учащиеся должны понимать, что сумму, разность, произведение и частное дробей всегда можно представить в виде дроби. Приобретаемые в данной теме умения выполнять сложение, вычитание, умножение и деление дробей являются опорными в преобразованиях дробных выражений. Поэтому им следует уделить особое внимание. Нецелесообразно переходить к комбинированным заданиям на все действия с дробями прежде, чем будут усвоены основные алгоритмы. При нахождении значений дробей даются задания на вычисления с помощью калькулятора. В данной теме расширяются сведения о статистических характеристиках. Вводится понятие среднего гармонического ряда положительных чисел. Изучение темы завершается рассмотрением свойств графика функции 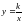 .
.
2. Четырёхугольники (20 ч).
Определение четырехугольника. Параллелограмм и его свойства Признаки параллелограмма. Прямоугольник, ромб, квадрат и их свойства. Теорема Фалеса. Средняя линия треугольника. Трапеция. Средняя линия трапеции. Пропорциональные отрезки.
Основная цель: дать учащимся систематизированные сведения о четырехугольниках и их свойствах.
Вводимые при изучении темы сведения о различных видах четырехугольников и их свойствах играют важную роль в изучении последующего материала. Основное внимание следует направить на решения задач, в ходе которых отрабатываются практические умения применять свойства и признаки параллелограмма и его частных видов, необходимые для распознавания конкретных видов четырехугольников и вычисления их элементов.
Рассматриваемая в теме теорема Фалеса (теорема о пропорциональных отрезках) играет вспомогательную роль в построении курса. Воспроизведения ее доказательства необязательно требовать от учащихся. Примером применения теоремы Фалеса является доказательство теоремы о средней линии треугольника. Теорема о пропорциональных отрезках используется в доказательстве теоремы о косинусе угла прямоугольного треугольника.
3. Квадратные корни (22 ч).
Понятие об иррациональных числах. Общие сведения о действительных числах. Квадратный корень. Понятие о нахождении приближенного значения квадратного корня. Свойства квадратных корней. Преобразования выражений, содержащих квадратные корни. Функция 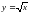 ее свойства и график.
ее свойства и график.
Основная цель: систематизировать сведения о рациональных числах и дать представление об иррациональных числах, расширив тем самым понятие о числе; выработать умение выполнять преобразования выражений, содержащих квадратные корни.
В данной теме учащиеся получают начальное представление о понятии действительного числа. С этой целью обобщаются известные учащимся сведения о рациональных числах. При введении понятия корня полезно ознакомить учащихся с нахождением корней с помощью калькулятора.
Основное внимание уделяется понятию арифметического квадратного корня и свойствам арифметических квадратных корней. Доказываются теоремы о корне из произведения и дроби, а также тождество 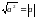 , которые получают применение в преобразованиях выражений, содержащих квадратные корни. Специальное внимание уделяется освобождению от иррациональности в знаменателе дроби в выражениях вида
, которые получают применение в преобразованиях выражений, содержащих квадратные корни. Специальное внимание уделяется освобождению от иррациональности в знаменателе дроби в выражениях вида 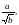
 . Умение преобразовывать выражения, содержащие корни, часто используется как в самом курсе алгебры, так и в курсах геометрии, алгебры и начал анализа.
. Умение преобразовывать выражения, содержащие корни, часто используется как в самом курсе алгебры, так и в курсах геометрии, алгебры и начал анализа.
Продолжается работа по развитию функциональных представлений учащихся. Рассматриваются функция 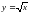 , ее свойства и график. При изучении функции
, ее свойства и график. При изучении функции 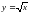 показывается ее взаимосвязь с функцией
показывается ее взаимосвязь с функцией 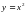 , где x ≥ 0.
, где x ≥ 0.
4. Теорема Пифагора (16 ч).
Синус, косинус и тангенс острого угла прямоугольного треугольника. Теорема Пифагора. Неравенство треугольника. Перпендикуляр и наклонная. Соотношение между сторонами и углами в прямоугольном треугольнике. Значения синуса, косинуса и тангенса некоторых углов.
Основная цель: сформировать аппарат решения прямоугольных треугольников, необходимый для вычисления элементов геометрических фигур на плоскости и в пространстве.
Изучение теоремы Пифагора позволяет существенно расширить круг геометрических задач, давая вместе с признаками равенства треугольников достаточно мощный аппарат решения задач.
Большое внимание в данной теме уделяется вопросам, связанным с решением прямоугольных треугольников. Для этого необходимо прочное усвоение определений синуса, косинуса и тангенса острого угла.В ходе решения задач усваиваются основные алгоритмы решения прямоугольных треугольников, при проведении практических вычислений вырабатываются навыки нахождения с помощью таблиц или калькуляторов значений синуса, косинуса и тангенса угла, а в ряде задач используются значения синуса, косинуса и тангенса углов 30°, 45 , 60°.
Соответствующие умения являются опорными для решения вычислительных задач и доказательств ряда теорем в курсе планиметрии и стереометрии. Кроме того, они используются и в курсе физики. Поэтому необходимо добиться прочных навыков практического применения этих фактов в решении вычислительных задач. При изучении данной темы широко используются и получают дальнейшее развитие такие навыки и алгебраические умения учащихся, как решение квадратных уравнений, извлечение квадратных корней, преобразования алгебраических уравнений.
В конце темы рассматривается теорема о неравенстве треугольника. Тем самым пополняются знания учащихся о свойствах расстояний между точками.
5. Квадратные уравнения ( 23 ч).
Квадратное уравнение. Формула корней квадратного уравнения. Решение рациональных уравнений. Решение задач, приводящих к квадратным уравнениям и простейшим рациональным уравнениям.
Основная цель: выработать умения решать квадратные уравнения и простейшие рациональные уравнения и применять их к решению задач.
В начале темы приводятся примеры решения неполных квадратных уравнений. Этот материал систематизируется. Рассматриваются алгоритмы решения неполных квадратных уравнений различного вида.
Основное внимание следует уделить решению уравнений вида ах2 + bх + с = 0, где а ≠ 0, с использованием формулы корней. В данной теме учащиеся знакомятся с формулами Виета, выражающими связь между корнями квадратного уравнения и его коэффициентами. Они используются в дальнейшем при доказательстве теоремы о разложении квадратного трехчлена на линейные множители.
Учащиеся овладевают способом решения дробных рациональных уравнений, который состоит в том, что решение таких уравнений сводится к решению соответствующих целых уравнений с последующим исключением посторонних корней.
Изучение данной темы позволяет существенно расширить аппарат уравнений, используемых для решения текстовых задач.
6. Декартовы координаты на плоскости (14 ч).
Прямоугольная система координат на плоскости. Координаты середины отрезка. Расстояние между точками. Уравнения прямой и окружности. Координаты точки пересечения прямых. График линейной функции. Пересечение прямой с окружностью. Синус, косинус и тангенс углов от 0° до 180°.
Основная цель: обобщить и систематизировать представления учащихся о декартовых координатах; развить умение применять алгебраический аппарат при решении геометрических задач.
В начале темы вводится определение декартовых координат, выводятся формулы для нахождения координаты середины отрезка и расстояния между точками. Рассматриваются уравнения окружности и прямой и способы нахождения с их помощью координат точки пересечения прямых, прямой с окружностью. В данной теме демонстрируется эффективность применения формул для координат середины отрезка, расстояния между точками, уравнений окружности и прямой в конкретных геометрических задачах, тем самым дается представление об изучении геометрических фигур с помощью методов алгебры.
7. Неравенства (19 ч).
Числовые неравенства и их свойства. Почленное сложение и умножение числовых неравенств. Погрешность и точность приближения. Линейные неравенства с одной переменной и их системы.
Основная цель: ознакомить учащихся с применением неравенств для оценки значений выражений, выработать умение решать линейные неравенства с одной переменной и их системы.
Свойства числовых неравенств составляют ту базу, на которой основано решение линейных неравенств с одной переменной. Теоремы о почленном сложении и умножении неравенств находят применение при выполнении простейших упражнений на оценку выражений по методу границ. Вводятся понятия абсолютной погрешности и точности приближения, относительной погрешности.
В связи с решением линейных неравенств с одной переменной дается понятие о числовых промежутках, вводятся соответствующие названия и обозначения. Рассмотрению систем неравенств с одной переменной предшествует ознакомление учащихся с понятиями пересечения и объединения множеств. При решении неравенств используются свойства равносильных неравенств, которые разъясняются на конкретных примерах. Особое внимание следует уделить отработке умения решать простейшие неравенства вида ахb, ахb, остановившись специально на случае, когда а0.
В этой теме рассматривается также решение систем двух линейных неравенств с одной переменной, в частности таких, которые записаны в виде двойных неравенств.
8. Движение (9 ч).
Движение и его свойства. Симметрия относительно точки и прямой. Поворот. Параллельный перенос и его свойства. Понятие о равенстве фигур.
Основная цель: познакомить учащихся с примерами геометрических преобразований.
Поскольку в дальнейшем движения не применяются в качестве аппарата для решения задач и изложения теории, можно рекомендовать изучение материала в ознакомительном порядке, т.е. не требовать от учащихся воспроизведения доказательств, Однако основные понятия — симметрия относительно точки и прямой, параллельный перенос — учащиеся должны усвоить на уровне практических применений.
9. Степень с целым показателем (10 ч).
Степень с целым показателем и её свойства. Стандартный вид числа. Начальные сведения об организации статистических исследований.
Основная цель: выработать умение применять свойства степени с целым показателем в вычислениях и преобразованиях, сформировать начальные представления о сборе и группировке статистических данных, их наглядной интерпретации.
В этой теме формулируются свойства степени с целым показателем. Метод доказательства этих свойств показывается на примере умножения степеней с одинаковыми основаниями. Дается понятие о записи числа в стандартном виде. Приводятся примеры использования такой записи в физике, технике и других областях знаний.
10. Векторы ( 11 ч).
Вектор. Абсолютная величина и направление вектора. Равенство векторов. Координаты вектора. Сложение векторов и его свойства. Умножение вектора на число. [Коллинеарные векторы.] Скалярное произведение векторов. Угол между векторами. [Проекция на ось. Разложение вектора по координатным осям.]
Основная цель: познакомить учащихся с элементами векторной алгебры и их применением для решения геометрических задач; сформировать умение производить операции над векторами.
Основное внимание следует уделить формированию практических умений учащихся, связанных с вычислением координат вектора, его абсолютной величины, выполнением сложения и вычитания векторов, умножения вектора на число. Наряду с операциями над векторами в координатной форме следует уделить большое внимание операциям в геометрической форме. Действия над векторами в координатной и геометрической формах используются при параллельном изучении курса физики.
11. Элементы статистики (5 ч)
Учащиеся получают начальные представления об организации статистических исследований. Они знакомятся с понятиями генеральной и выборочной совокупности. Приводятся примеры представления статистических данных в виде таблиц частот и относительных частот. Учащимся предлагаются задания на нахождение по таблице частот таких статистических характеристик, как среднее арифметическое, размах и мода. Рассматривается вопрос о наглядной интерпретации статистической информации. Известные учащимся способы наглядного представления статистических данных с помощью столбчатых и круговых диаграмм расширяются за счёт введения таких понятий, как полигон и гистограмма.
12. Повторение ( 32 ч).
Основная цель: повторение, обобщение и систематизация знаний, умений и навыков за курс математики 8 класса.
Календарно-тематическое планирование, 8 класс
|
№ урока | Дата |
РАЗДЕЛ |
ТЕМА УРОКА
|
ВИД КОНТРОЛЯ
|
| По плану | Фактически |
| 1. | 01.09 |
| Повторение материала 7 класса | Степень с натуральным показателем. Одночлен. Многочлены и действия над ними | текущий |
| 2. | 02.09 |
| Формулы сокращенного умножения. | текущей |
| 3. | 03.09 |
| Линейное уравнение с одной переменной. Системы линейных уравнений с двумя переменными | текущий |
| 4. | 03.09 |
| Решение задач на составление уравнения или системы уравнений. | текущий |
| 5. | 04.09 |
| Решение геометрических задач. | текущий |
| 6 | 07.09 |
| Входная контрольная работа | периодический |
| 7 | 08.09 |
| Глава 1. Рациональные дроби и их свойства (25 часов) | Рациональные выражения. | текущий |
| 8 | 09.09 |
| Рациональные выражения. | текущий |
| 9 | 10.09 |
| Основное свойство дроби. | текущий |
| 10 | 10.09 |
| Сокращение дробей. | текущий |
| 11 | 11.09 |
| Сокращение дробей. | предварительный |
| 12 | 14.09 |
| Сложение и вычитание дробей с одинаковыми знаменателями. | текущий |
| 13 | 15.09 |
| Сложение и вычитание дробей с одинаковыми знаменателями. | текущий |
| 14 | 16.09 |
| Сложение и вычитание дробей с одинаковыми знаменателями. | предварительный |
| 15 | 17.09 |
| Сложение и вычитание дробей с разными знаменателями. | текущий |
| 16 | 17.09 |
| Сложение и вычитание дробей с разными знаменателями. | предварительный |
| 17 | 18.09 |
| Сложение и вычитание дробей с разными знаменателями. | текущий |
| 18 | 21.09 |
| К. р. № 1 «Сложение и вычитание дробей» | периодический |
| 19 | 22.09 |
| Умножение дробей. | текущий |
| 20 | 23.09 |
| Возведение дроби в степень. | текущий |
| 21 | 24.09 |
| Возведение дроби в степень | текущий |
| 22 | 24.09 |
| Деление дробей | текущий |
| 23 | 25.09 |
| Деление дробей. | предварительный |
| 24 | 28.09 |
| Преобразование рациональных выражений | текущий |
| 25 | 29.09 |
| Преобразование рациональных выражений | текущий |
| 26 | 30.09 |
| Преобразование рациональных выражений | текущий |
| 27 | 01.10 |
| Преобразование рациональных выражений | предварительный |
| 28 | 01.10 |
| Функция у = k / x и ее график. | текущий |
| 29 | 02.10 |
| Функция у = k / x и ее график. | текущий |
| 30 | 05.10 |
| Функция у = k / x и ее график. | текущий |
| 31 | 06.10 |
| К. р. № 2 «Произведение и частное дробей» | периодический |
| 32 | 07.10 |
| Глава 2. Четырехуголь-ники ( 20 часов) | Определение четырехугольника. | текущий |
| 33 | 08.10 |
| Параллелограмм | текущий |
| 34 | 08.10 |
| Свойство диагоналей параллелограмма. | текущий |
| 35 | 09.10 |
| Свойство противоположных сторон и углов параллелограмма. | предварительный |
| 36 | 12.10 |
| Прямоугольник. | текущий |
| 37 | 13.10 |
| Ромб. | текущий |
| 38 | 14.10 |
| Квадрат. | текущий |
| 39 | 15.10 |
| Решение задач. | текущий |
| 40 | 15.10 |
| Решение задач. | предварительный |
| 41 | 16.10 |
| К. р. № 3 «Четырехугольники» | периодический |
| 42 | 19.10 |
| Теорема Фалеса. | текущий |
| 43 | 20.10 |
| Средняя линия треугольника. | текущий |
| 44 | 21.10 |
| Средняя линия треугольника. | предварительный |
| 45 | 22.10 |
| Трапеция. | текущий |
| 46 | 22.10 |
| Средняя линия трапеции. | текущий |
| 47 | 23.10 |
| Теорема о пропорциональных отрезках. | текущий |
| 48 | 26.10 |
| Построение четвертого пропорционального отрезка | текущий |
| 49 | 27.10 |
| Решение задач. | предварительный |
| 50 | 28.10 |
| Решение задач | предварительный |
| 51 | 29.10 |
| К. р. № 4 «Четырехугольники» | периодический |
| 52 | 29.10 |
| Глава 3. Квадратные корни (22 часа)
| Рациональные и иррациональные числа. | текущий |
| 53 | 30.10 |
| Рациональные и иррациональные числа. | текущий |
| 54 | 09.11 |
| Рациональные и иррациональные числа. | текущий |
| 55 | 10.11 |
| Квадратные корни. | текущий |
| 56 | 11.11 |
| Арифметический квадратный корень. | предварительный |
| 57 | 12.11 |
| Уравнение х2 = а. | текущий |
| 58 | 12.11 |
| Нахождение приближенных значений квадратного корня. | текущий |
| 59 | 13.11 |
| Функция у = √х и ее график | текущий |
| 60 | 16.11 |
| Функция у = √х и ее график | предварительный |
| 61 | 17.11 |
| Квадратный корень из произведения. | текущий |
| 62 | 18.11 |
| Квадратный корень из дроби. | текущий |
| 63 | 19.11 |
| Квадратный корень из степени. | предварительный |
| 64 | 19.11 |
| Квадратный корень из произведения, дроби, степени. | текущий |
| 65 | 20.11 |
| К. р. № 5 «Квадратные корни». | периодический |
| 66 | 23.11 |
| Вынесение множителя из-под знака корня. | текущий |
| 67 | 24.11 |
| Внесение множителя под знак корня | текущий |
| 68 | 25.11 |
| Вынесение и внесение множителя из-под знака корня. | предварительный |
| 69 | 26.11 |
| Преобразование выражений, содержащих квадратные корни | текущий |
| 70 | 26.11 |
| Преобразование выражений, содержащих квадратные корни | текущий |
| 71 | 27.11 |
| Преобразование выражений, содержащих квадратные корни | предварительный |
| 72 | 30.11 |
| Преобразование выражений, содержащих квадратные корни | текущий |
| 73 | 01.12 |
| К. р. № 6 «Применение свойств арифметического квадратного корня» | периодический |
| 74 | 02.12 |
| Глава 4. Теорема Пифагора ( 16 часов) | Косинус угла | текущий |
| 75 | 03.12 |
| Теорема Пифагора. | текущий |
| 76 | 03.12 |
| Египетский треугольник. | текущий |
| 77 | 04.12 |
| Перпендикуляр и наклонная. | предварительный |
| 78 | 07.12 |
| Неравенство треугольника. | текущий |
| 79 | 08.12 |
| Решение задач | текущий |
| 80 | 09.12 |
| К. р. № 7 «Теорема Пифагора» | периодический |
| 81 | 10.12 |
| Соотношения между сторонами и углами в прямоугольном треугольнике. | текущий |
| 82 | 10.12 |
| Соотношения между сторонами и углами в прямоугольном треугольнике. | текущий |
| 83 | 11.12 |
| Основные тригонометрические тождества. | текущий |
| 84 | 14.12 |
| Основные тригонометрические тождества. | предварительный |
| 85 | 15.12 |
| Значения синуса, косинуса, тангенса некоторых углов. | текущий |
| 86 | 16.12 |
| Значения синуса, косинуса, тангенса некоторых углов. | текущий |
| 87 | 17.12 |
| Изменение синуса, косинуса и тангенса при возрастании угла. | текущий |
| 88 | 17.12 |
| Решение задач. | предварительный |
| 89 | 18.12 |
| К. р. № 8 «Соотношения между сторонами и углами треугольника» | периодический |
| 90 | 21.12 |
| Глава 5. Квадратные уравнения (23 часа) | Определение квадратного уравнения | текущий |
| 91 | 22.12 |
| Неполные квадратные уравнения. | текущий |
| 92 | 23.12 |
| Решение квадратных уравнений по формуле | текущий |
| 93 | 24.12 |
| Решение квадратных уравнений по формуле | текущий |
| 94 | 24.12 |
| Решение квадратных уравнений по формуле | предварительный |
| 95 | 25.12 |
| Решение квадратных уравнений по формуле | текущий |
| 96 | 28.12 |
| Решение задач с помощью квадратных уравнений | текущий |
| 97 | 29.12 |
| Решение задач с помощью квадратных уравнений | предварительный |
| 98 | 30.12 |
| Решение задач с помощью квадратных уравнений | текущий |
| 99 | 11.01 |
| Теорема Виета. | текущий |
| 100 | 12.01 |
| Теорема Виета. | текущий |
| 101 | 13.01 |
| К. р. № 9 «Квадратные уравнения» | периодический |
| 102 | 14.01 |
| Решение дробных рациональных уравнений | текущий |
| 103 | 14.01 |
| Решение дробных рациональных уравнений | текущий |
| 104 | 15.01 |
| Решение дробных рациональных уравнений | предварительный |
| 105 | 18.01 |
| Решение дробных рациональных уравнений | текущий |
| 106 | 19.01 |
| Решение задач с помощью рациональных уравнений | текущий |
| 107 | 20.01 |
| Решение задач с помощью рациональных уравнений | текущий |
| 108 | 21.01 |
| Решение задач с помощью рациональных уравнений | текущий |
| 109 | 21.01 |
| Графический способ решения уравнений | текущий |
| 110 | 22.01 |
|
| Графический способ решения уравнений | предварительный |
| 111 | 25.01 |
| Графический способ решения уравнений | текущий |
| 112 | 26.01 |
| К. р. № 10 «Дробные рациональные уравнения» | периодический |
| 113 | 27.01 |
| Глава 6. Декартовы координаты на плоскости (14 часов) | Определение декартовых координат. | текущий |
| 114 | 28.01 |
| Координаты середины отрезка. | текущий |
| 115 | 28.01 |
| Расстояние между точками. | предварительный |
| 116 | 29.01 |
| Уравнение окружности. | текущий |
| 117 | 01.02 |
| Уравнение прямой. | текущий |
| 118 | 02.02 |
| Координаты точки пересечения прямых. | текущий |
| 119 | 03.02 |
| Расположение прямой относительно системы координат. | текущий |
| 120 | 04.02 |
| Угловой коэффициент в уравнении прямой. График линейной функции. | текущий |
| 121 | 04.02 |
| Пересечение прямой с окружностью. | текущий |
| 122 | 05.02 |
| Определение синуса, косинуса, тангенса любого угла от 00до 180 0 | предварительный |
| 123 | 08.02 |
| Определение синуса, косинуса, тангенса любого угла от 00до 180 0. | текущий |
| 124 | 09.02 |
| К. р. № 11 «Декартовы координаты на плоскости» | периодический |
| 125 | 10.02 |
| Глава 7. Неравенства (19 часов) | Числовые неравенства. | текущий |
| 126 | 11.02 |
| Свойства числовых неравенств. | текущий |
| 127 | 11.02 |
| Свойства числовых неравенств. | предварительный |
| 128 | 12.02 |
| Свойства числовых неравенств. | текущий |
| 129 | 15.02 |
| Сложение числовых неравенств. | текущий |
| 130 | 16.02 |
| Умножение числовых неравенств. | предварительный |
| 131 | 17.02 |
| Умножение числовых неравенств. | текущий |
| 132 | 18.02 |
| К. р. № 12 «Числовые неравенства и их свойства» | периодический |
| 133 | 18.02 |
| Числовые промежутки | текущий |
| 134 | 19.02 |
| Числовые промежутки | текущий |
| 135 | 22.02 |
| Решение неравенств с одной переменной | текущий |
| 136 | 23.02 |
| Решение неравенств с одной переменной | текущий |
| 137 | 24.02 |
| Решение неравенств с одной переменной. | текущий |
| 138 | 25.02 |
| Решение неравенств с одной переменной | предварительный |
| 139 | 25.02 |
| Решение неравенств с одной переменной | текущий |
| 140 | 26.02 |
| Решение систем неравенств с одной переменной | текущий |
| 141 | 29.02 |
| Решение систем неравенств с одной переменной | текущий |
| 142 | 01.03 |
| Решение систем неравенств с одной переменной | текущий |
| 143 | 02.03 |
| К. р. № 13 «Неравенства с одной переменной и их системы» | периодический |
| 144 | 03.03 |
| Глава 8. Движения (9 часов)
| Преобразование фигур. Свойства движения. | текущий |
| 145 | 03.03 |
| Симметрия относительно точки. | предварительный |
| 146 | 04.03 |
| Симметрия относительно прямой. | предварительный |
| 147 | 07.03 |
| Поворот | предварительный |
| 148 | 08.03 |
| Параллельный перенос и его свойства. | текущий |
| 149 | 09.03 |
| Существование и единственность параллельного переноса | предварительный |
| 150 | 10.03 |
| Сонаправленность полупрямых. | текущий |
| 151 | 10.03 |
| Геометрические преобразования на практике. Равенство фигур | текущий |
| 152 | 11.03 |
| К. р. № 14 «Движение» | периодический |
| 153 | 14.03 |
| Глава 9. Степень с целым показателем (10 часов) | Определение степени с целым отрицательным показателем. | текущий |
| 154 | 15.03 |
| Определение степени с целым отрицательным показателем. | текущий |
| 155 | 16.03 |
| Свойства степени с целым показателем. | текущий |
| 156 | 17.03 |
| Свойства степени с целым показателем. | текущий |
| 157 | 17.03 |
| Свойства степени с целым показателем. | текущий |
| 158 | 18.03 |
| Свойства степени с целым показателем. | предварительный |
| 159 | 21.03 |
| Стандартный вид числа. | текущий |
| 160 | 22.03 |
| Стандартный вид числа. | текущий |
| 161 | 23.03 |
| Запись приближенных значений | предварительный |
| 162 | 04.04 |
| К. р. № 15 «Степень с целым показателем» | периодический |
| 163 | 05.04 |
| Глава 10. Векторы (11 часов)
| Абсолютная величина и направление вектора. | текущий |
| 164 | 06.04 |
| Равенство векторов. Координаты вектора | текущий |
| 165 | 07.04 |
| Сложение векторов. Вычитание векторов. | текущий |
| 166 | 07.04 |
| Сложение сил. | текущий |
| 167 | 08.04 |
| Умножение вектора на число. | предварительный |
| 168 | 11.04 |
| Разложение вектора по двум неколлинеарным векторам. | предварительный |
| 169 | 12.04 |
| Скалярное произведение векторов. | предварительный |
| 170 | 13.04 |
| Скалярное произведение векторов. | предварительный |
| 171 | 14.04 |
| Разложение вектора по координатным векторам. | текущий |
| 172 | 14.04 |
| Разложение вектора по координатным векторам. | периодический |
| 173 | 15.04 |
| К. р. № 16 «Векторы» | периодический |
| 174 | 18.04 |
| Глава 12. Элементы статистики (5 часов) | Сбор и группировка статистических данных. | текущий |
| 175 | 19.04 |
| Сбор и группировка статистических данных. | текущий |
| 176 | 20.04 |
| Наглядное представление статистической информации | текущий |
| 177 | 21.04 |
| Наглядное представление статистической информации | текущий |
| 178 | 21.04 |
| Наглядное представление статистической информации | текущий |
| 179 | 22.04 |
| Повторение за курс 8 класса (32 часа) | Действия с рациональными дробями |
|
| 180 | 25.04 |
| Действия с рациональными дробями | итоговый |
| 181 | 26.04 |
| Квадратные уравнения и из системы |
|
| 182 | 27.04 |
| Задачи на составление квадратного уравнения или системы |
|
| 183 | 28.04 |
| Задачи на составление квадратного уравнения или системы |
|
| 184 | 28.04 |
| Задачи на составление дробно – рационального уравнения. |
|
| 185 | 29.04 |
| Задачи на составление дробно – рационального уравнения. |
|
| 186 | 02.05 |
| Преобразование выражений, содержащих корни |
|
| 187 | 03.05 |
| Преобразование выражений, содержащих корни |
|
| 188 | 05.05 |
| Преобразование выражений, содержащих корни |
|
| 189 | 06.05 |
| Функции и их графики |
|
| 190 | 06.05 |
| Функции и их графики |
|
| 191 | 09.05 |
| Преобразование выражений, содержащие степень |
|
| 192 | 10.05 |
| Преобразование выражений, содержащие степень |
|
| 193 | 11.05 |
| Преобразование выражений, содержащие степень |
|
| 194 | 12.05 |
| Неравенства, системы неравенств |
|
| 195 | 12.05 |
| Неравенства, системы неравенств |
|
| 196 | 13.05 |
| Неравенства, системы неравенств |
|
| 197 | 16.05 |
| Решение геометрических задач |
|
| 198 | 17.05 |
| Решение геометрических задач |
|
| 199 | 18.05 |
| Итоговая контрольная работа |
|
| 200 | 18.05 |
| Итоговая контрольная работа |
|
| 201 | 19.05 |
| Уравнения, содержащие модуль |
|
| 202 | 20.05 |
| Уравнения, содержащие модуль |
|
| 203 | 23.05 |
| Графики, содержащие модуль |
|
| 204 | 24.05 |
| Графики, содержащие модуль |
|
| 205 | 25.05 |
| Итоговый урок за курс 8 класса |
|
| 206 | 26.05 |
| Резерв |
|
| 207 | 26.05 |
| Резерв |
|
| 208 | 27.05 |
| Резерв |
|
| 209 | 30.05 |
| Резерв |
|
| 210 | 31.05 |
| Резерв |
|
Описание материально-технического обеспечения образовательного процесса.
Алгебра-8: учебник / Ю.Н.Макарычев, Н.Г.Миндюк, К.Н.Нешков –М.: Просвещение, 2014.
Изучение алгебры в 7—9 классах: пособие для учителей / Ю.Н.Макарычев, Н.Г.Миндюк, С.Б.Суворова и др. — М.: Просвещение, 2011.
Уроки алгебры в 8 классе: книга для учителя / В.И.Жохов, Л.Б.Крайнева. — М.: Просвещение, 2011.
Дидактические материалы по алгебре для 8 класса / Л.И.Звавич, Л.В.Кузнецова, С.Б.Суворова. — М.: Просвещение, 2011.
Алгебра. Тематические тесты. 8 класс / Ю.П.Дудницын и др.. — М.: Просвещение, 2011.
Геометрия 7-9: учебник / А.В.Погорелов. — М.: Просвещение, 2013.
Геометрия 7-9: книга для учителя / В.И.Жохов, Г.Д.Карташева, Л.Б.Крайнева. — М.: Просвещение, 2014
Геометрия. Рабочая тетрадь, 8 класс Ю.П.Дудницын. - М.: Просвещение, 2011.
Контрольные работы по геометрии для 7 – 9 классов:книга для учителя / Ю.П.Дудницын, В.Л.Кронгауз. – М.: Просвещение, 2011.
Самостоятельные и контрольные работы по алгебре и геометрии для 8 класса / А.П.Ершова, В.В.Голобородько, А.С.Ершова.— М: Илекса, 2014.
Программы общеобразовательных учреждений. Геометрия. 7 – 9 классы / Т.А. Бурмистрова. – М.: Просвещение, 2011.
Программы общеобразовательных учреждений. Алгебра 7 – 9 классы / Т.А. Бурмистрова– М.: Просвещение, 2011.
13







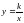 и ее график.
и ее график.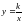 .
.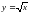 ее свойства и график.
ее свойства и график.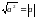 , которые получают применение в преобразованиях выражений, содержащих квадратные корни. Специальное внимание уделяется освобождению от иррациональности в знаменателе дроби в выражениях вида
, которые получают применение в преобразованиях выражений, содержащих квадратные корни. Специальное внимание уделяется освобождению от иррациональности в знаменателе дроби в выражениях вида 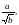
 . Умение преобразовывать выражения, содержащие корни, часто используется как в самом курсе алгебры, так и в курсах геометрии, алгебры и начал анализа.
. Умение преобразовывать выражения, содержащие корни, часто используется как в самом курсе алгебры, так и в курсах геометрии, алгебры и начал анализа.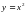 , где x ≥ 0.
, где x ≥ 0.









