Муниципальное бюджетное общеобразовательное учреждение
«Лицей № 6»
Утверждена приказом руководителя
образовательного учреждения
№ ______ от ___________________
Директор МОУ «Лицей № 6»
________________Купцов А.М.
Рабочая программа
учебного курса по математике 10 а, 10 б класс
(7 часов в неделю, всего 245 часов)
Заслушана на ШМО
28.08. 2021г.
Рук. ШМО ____ /Ларькова Т.П./
Согласована
30.08.2021 г.
Председатель МСШ ____ /Подзорова А.А./
Составитель: ШМО учителей математики
Северобайкальск
2021 г
Планируемые результаты освоения учебного предмета
Изучение математики по данной программе способствует формированию у учащихся личностных, метапредметных и предметных результатов обучения, соответствующих требованиям Федерального государственного образовательного стандарта среднего общего образования.
Личностные результаты:
воспитание российской гражданской идентичности: патриотизма, уважения к Отечеству, осознание вклада отечественных учёных в развитие мировой науки;
формирование мировоззрения, соответствующего современному уровню развития науки и общественной практики;
ответственное отношение к обучению, готовность и способность к саморазвитию и самообразованию на протяжении всей жизни; сознательное отношение к непрерывному образованию как условию успешной профессиональной и общественной деятельности;
осознанный выбор будущей профессиональной деятельности на базе ориентировки в мире профессий и профессиональных предпочтений; отношение к профессиональной деятельности как к возможности участия в решении личных, общественных, государственных и общенациональных проблем; формирование уважительного отношения к труду, развитие опыта участия в социально значимом труде;
умение контролировать, оценивать и анализировать процесс и результат учебной и математической деятельности;
умение управлять своей познавательной деятельностью;
умение взаимодействовать с одноклассниками, детьми младшего возраста и взрослыми в образовательной, общественно полезной, учебно-исследовательской, проектной и других видах деятельности;
критичность мышления, инициатива, находчивость, активность при решении математических задач.
Метапредметные результаты:
умение самостоятельно определять цели своей деятельности, ставить и формулировать для себя новые задачи в учёбе;
умение соотносить свои действия с планируемыми результатами, осуществлять контроль своей деятельности в процессе достижения результата, определять способы действий в рамках предложенных условий и требований, корректировать свои действия в соответствии с изменяющейся ситуацией;
умение самостоятельно принимать решения, проводить анализ своей деятельности, применять различные методы познания;
владение навыками познавательной, учебно-исследовательской и проектной деятельности;
формирование понятийного аппарата, умения создавать обобщения, устанавливать аналогии, классифицировать, самостоятельно выбирать основания и критерии для классификации;
умение устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение (индуктивное, дедуктивное и по аналогии) и делать выводы;
формирование компетентности в области использования информационно-коммуникационных технологий;
умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни;
умение самостоятельно осуществлять поиск в различных источниках, отбор, анализ, систематизацию и классификацию информации, необходимой для решения математических проблем, представлять её в понятной форме; принимать решение в условиях неполной или избыточной, точной или вероятностной информации; критически оценивать и интерпретировать информацию, получаемую из различных источников;
умение использовать математические средства наглядности (графики, таблицы, схемы и др.) для иллюстрации, интерпретации, аргументации;
умение выдвигать гипотезы при решении задачи, понимать необходимость их проверки;
понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом.
Предметные результаты:
осознание значения математики в повседневной жизни человека;
представление о математической науке как сфере математической деятельности, об этапах её развития, о её значимости для развития цивилизации;
умение описывать явления реального мира на математическом языке; представление о математических понятиях и математических моделях как о важнейшем инструментарии, позволяющем описывать и изучать разные процессы и явления;
представление об основных понятиях, идеях и методах алгебры и математического анализа;
представление о процессах и явлениях, имеющих вероятностный характер, о статистических закономерностях в реальном мире, об основных понятиях элементарной теории вероятностей; умение находить и оценивать вероятности наступления событий в простейших практических ситуациях и основные характеристики случайных величин;
владение методами доказательств и алгоритмами решения; умение их применять, проводить доказательные рассуждения в ходе решения задач;
практически значимые математические умения и навыки, способность их применения к решению математических и нематематических задач, предполагающие умение:
выполнять вычисления с действительными и комплексными числами;
решать рациональные, иррациональные, показательные, степенные и тригонометрические уравнения, неравенства, системы уравнений и неравенств;
решать текстовые задачи арифметическим способом, с помощью составления и решения уравнений, систем уравнений и неравенств;
использовать алгебраический язык для описания предметов окружающего мира и создания соответствующих математических моделей;
выполнять тождественные преобразования рациональных, иррациональных, показательных, степенных, тригонометрических выражений;
выполнять операции над множествами;
исследовать функции с помощью производной и строить их графики;
вычислять площади фигур и объёмы тел с помощью определённого интеграла;
проводить вычисления статистических характеристик, выполнять приближённые вычисления;
решать комбинаторные задачи;
владение навыками использования компьютерных программ при решении математических задач.
Требования к математической подготовке
Повторение и расширение сведений о функции
Формулировать определения наибольшего и наименьшего значений функции, чётной и нечётной функций. Формулировать теоремы о свойствах графиков чётных и нечётных функций. Находить наибольшее и наименьшее значения функции на множестве по её графику. Исследовать функцию, заданную формулой, на чётность. Строить графики функций, используя чётность или нечётность. Формулировать определение обратимой функции. Распознавать обратимую функцию по её графику. Устанавливать обратимость функции по её возрастанию или убыванию. Формулировать определение взаимно обратных функций. Проверять, являются ли две данные функции взаимно обратными. Находить обратную функцию к данной обратимой функции. По графику данной функции строить график обратной функции. Устанавливать возрастание (убывание) обратной функции по возрастанию (убыванию) данной функции.
Формулировать определения области определения уравнений (неравенств), равносильных уравнений (неравенств), уравнений-следствий (неравенств-следствий), постороннего корня. Формулировать теоремы, описывающие равносильные преобразования уравнений (неравенств).
Выполнять геометрические преобразования графиков функций, связанные с параллельными переносами, растяжениями, сжатиями и симметриями, относительно координатных осей.
Применять метод равносильных преобразований для решения уравнений и неравенств. Находить область определения уравнений и неравенств. При-
менять метод следствий для решения уравнений.
Решать неравенства методом интервалов
Степенная функция
Формулировать определение степенной функции с целым показателем. Описывать свойства степенной функции с целым показателем, выделяя
случаи чётной и нечётной степени, а также натуральной, нулевой и целой отрицательной степени. Строить графики функций на основе графика степенной функции с целым показателем. Находить наибольшее и наименьшее значения степенной
функции с целым показателем на промежутке.
Формулировать определение корня (арифметического корня) n-й степени, а также теоремы о его свойствах, выделяя случаи корней чётной и нечётной степени. Находить области определения выражений, содержащих корни n-й степени. Решать уравнения, сводящиеся к уравнению xn = a. Выполнять тождественные преобразования выражений, содержащих корни n-й степени, в частности, выносить множитель из-под знака корня n-й степени, вносить множитель под знак корня n-й степени, освобождаться от иррациональности в знаменателе дроби. Описывать свойства функции 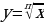 , выделяя случаи корней чётной и нечётной степени. Строить графики функций на основе графика функции
, выделяя случаи корней чётной и нечётной степени. Строить графики функций на основе графика функции 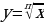
Формулировать определение степени с рациональным показателем, а также теоремы о её свойствах. Выполнять тождественные преобразования выражений, содержащих степени с рациональным показателем.
Распознавать иррациональные уравнения и неравенства. Формулировать теоремы, обосновывающие равносильность уравнений (неравенств) при возведении обеих частей данного уравнения (неравенства) в натуральную степень. Решать иррациональные уравнения методом равносильных преобразований и методом следствий. Решать иррациональные неравенства методом равносильных преобразованийигонометрические функции
Формулировать определение радианной меры угла. Находить радианную меру угла по его градусной мере и градусную меру угла по его радианной мере. Вычислять длины дуг окружностей.
Формулировать определения косинуса, синуса, тангенса и котангенса угла поворота. Выяснять знак значений тригонометрических функций.
Упрощать тригонометрические выражения, используя свойства чётности тригонометрических функций.
Формулировать определения периодической функции, её главного периода. Упрощать тригонометрические выражения, используя свойства периодичности тригонометрических функций.
Описывать свойства тригонометрических функций. Строить графики функций на основе графиков четырёх основных тригонометрических функций.
Преобразовывать тригонометрические выражения на основе соотношений между тригонометрическими функциями одного и того же аргумента.о значениям одной тригонометрической функции находить значения остальных тригонометрических функций того же аргумента.
Преобразовывать тригонометрические выражения на основе формул сложения. Опираясь на формулы сложения, доказывать формулы приведения, формулы двойных углов, формулы суммы и разности синусов (косинусов), формулы преобразования произведения тригонометрических функций в сумму. Преобразовывать тригонометрические выражения на основе формул приведения, формул двойных и половинных углов, формул суммы и разности синусов (косинусов), формул преобразования произведения тригонометрических функций в сумму
Тригонометрические уравнения и неравенства
Формулировать определения арккосинуса, арксинуса, арктангенса, арккотангенса. Находить значения обратных тригонометрических функций в отдельных табличных точках. Используя понятия арккосинуса, арксинуса, арктангенса, арккотангенса, решать простейшие тригонометрические уравнения.
Формулировать свойства обратных тригонометрических функций. Строить графики функций на основе графиков четырёх основных обратных тригонометрических функций. Упрощать выражения, содержащие обратные тригонометрические функции.
Распознавать тригонометрические уравнения и неравенства. Решать тригонометрические уравнения, сводящиеся к алгебраическим уравнениям, в частности, решать однородные тригонометрические уравнения первой и второй степени, а также решать тригонометрические уравнения, применяя метод разложения на множители.
Решать простейшие тригонометрические неравенства
Производная и ее применение.
Устанавливать существование предела функции в точке и находить его на основе графика функции. Различать графики непрерывных и разрывных функций.
Находить приращение аргумента и приращение функции в точке. Вычислять среднюю скорость движения материальной точки по закону её движения.
Формулировать определение производной функции в точке, правила вычисления производных. Находить производные функций, уравнения касательных графика функции, мгновенную скорость движения материальной точки. Использовать механический и геометрический смысл производной в задачах механики и геометрии.
Формулировать признаки постоянства, возрастания и убывания функции. Находить промежутки возрастания и убывания функции, заданной формулой.
Формулировать определения точки максимума и точки минимума, критической точки, теоремы, связывающие точки экстремума с производной. Находить точки экстремума функции, наибольшее и наименьшее значения функции на промежутке.
Исследовать свойства функции с помощью производной и строить график функций
Геометрия.
распознавать на чертежах и моделях пространственные формы; соотносить трехмерные объекты с их описаниями, изображениями;
описывать взаимное расположение прямых и плоскостей в пространстве, аргументировать свои суждения об этом расположении;
анализировать в простейших случаях взаимное расположение объектов в пространстве;
изображать основные многогранники и круглые тела; выполнять чертежи по условиям задач;
строить простейшие сечения куба, призмы, пирамиды;
решать планиметрические и простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей);
использовать при решении стереометрических задач планиметрические факты и методы;
проводить доказательные рассуждения в ходе решения задач;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни.
исследования (моделирования) несложных практических ситуаций на основе изученных формул и свойств фигур.
Содержание учебного курса
Алгебра
Отбор содержания обучения осуществляется на основе следующих дидактических принципов: систематизация знаний, полученных учащимися в основной школе; соответствие обязательному минимуму содержания образования в основной школе; усиление общекультурной направленности материала; учёт психолого-педагогических особенностей, актуальных для этого возрастного периода; создание условий для понимания и осознания воспринимаемого материала. В предлагаемом курсе математики выделяются несколько разделов.
Повторение и расширение сведений о функции (16 ч)
Наибольшее и наименьшее значение функции. Чётные и нечётные функции. Построение графиков функций с помощью геометрических преобразований. Обратная функция. Равносильные уравнения и неравенства. Метод интервалов.
Цель: повторить способ решения неравенств методом интервалов, выработать умение решать и преобразовывать графики функций с помощью геометрических преобразований и применять их при решении задач.
Степенная функция. (25 ч)
Степенная функция с натуральным и целым показателем. Определение корня n-й степени. Функция 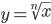 . Свойства корня n-й степени. Определение и свойства степени с рациональным показателем. Иррациональные уравнения. Метод равносильных преобразований для решения иррациональных уравнений. Иррациональные неравенства.
. Свойства корня n-й степени. Определение и свойства степени с рациональным показателем. Иррациональные уравнения. Метод равносильных преобразований для решения иррациональных уравнений. Иррациональные неравенства.
Цель: выработать умение читать и строить графики изучаемых функций; научиться решать иррациональные уравнений и неравенств, а также выполнять тождественные преобразования над выражениями.
Тригонометрическая функция (40 ч)
Радианная мера угла. Тригонометрические функции числового аргумента. Знаки значений тригонометрических функций. Чётность и нечётность тригонометрических функций. Периодичность функции. Свойства и графики функций 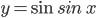 ,
, 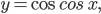
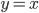 ,
, 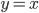 . Основные соотношения между тригонометрическими функциями одного и того же аргумента. Формулы сложения. Формулы приведения. Формулы двойного аргумента и половинного угла. Сумма и разность синусов (косинусов). Формулы преобразования произведения тригонометрических функций в сумму.
. Основные соотношения между тригонометрическими функциями одного и того же аргумента. Формулы сложения. Формулы приведения. Формулы двойного аргумента и половинного угла. Сумма и разность синусов (косинусов). Формулы преобразования произведения тригонометрических функций в сумму.
Цель: ознакомить обучающихся с тригонометрическими функциями и способами их преобразования.
Тригонометрические уравнения и неравенства (30 ч)
Уравнение 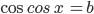 ,
, 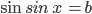 ,
, 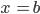 ,
, 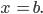 Функции
Функции 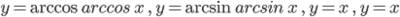 . Тригонометрические уравнения, сводящиеся к алгебраическим. Решение тригонометрических уравнений методом разложения на множители. Решение простейших тригонометрических неравенств.
. Тригонометрические уравнения, сводящиеся к алгебраическим. Решение тригонометрических уравнений методом разложения на множители. Решение простейших тригонометрических неравенств.
Цель: научить решать тригонометрические уравнения нового вида; познакомиться с функциями арксинуса, арккосинуса, арктангенса и араккотангенса и научить применять их при решении задач.
Производная и её применение (40 ч)
Представление о пределе функции в точке и о непрерывности функции в точке. Задачи о мгновенной скорости и касательной к графику функции. Понятие производной. Правила вычисления производных. Уравнение касательной. Признаки возрастания и убывания функции. Точки экстремума функции. Применение Производной при нахождении наибольшего и наименьшего значения функции. Построение графиков функций.
Цели: познакомиться с понятием предела, научиться составлять уравнение касательной и уметь исследовать функцию на монотонность и экстремумы.
Повторение и систематизация учебного материала (24ч)
Повторение и систематизация учебного материала за курс алгебры 10 класса.
Геометрия
§ 1. Аксиомы стереометрии и их простейшие следствия (6 часов)
Аксиомы стереометрии. Существование плоскости, проходящей через данную прямую и данную точку. Пересечение прямой с плоскостью. Существование плоскости, проходящей через три данные точки
§ 2. Параллельность прямых и плоскостей (16 часов)
Параллельные прямые в пространстве. Признак параллельности прямых. Признак параллельности прямой и плоскости. Признак параллельности плоскостей. Существование плоскости, параллельной данной плоскости. Свойства параллельных плоскостей. Параллельное проектирование. Изображение пространственных фигур на плоскости.
§ 3. Перпендикулярность прямых и плоскостей (20 часов)
Перпендикулярность прямых в пространстве. Признак перпендикулярности прямой и плоскости. Построение перпендикулярных прямой и плоскости. Свойства перпендикулярных прямой и плоскости. Перпендикуляр и наклонная. Теорема о трех перпендикулярах. Угол между прямой и плоскостью. Угол между плоскостями. Признак перпендикулярности плоскостей. Площадь ортогональной проекции многоугольника. Расстояние между скрещивающимися прямыми.
Многогранники (18ч).
. Многогранники. Сечения многогранников. Призма. Прямая и правильная призмы. Параллелепипед. Пирамида. Усеченная пирамида. Правильная пирамида. Правильные многогранники.
На материале, связанном с изучением пространственных геометрических фигур, повторяются и систематизируются знания учащихся о взаимном расположении точек, прямых и плоскостей в пространстве, об измерении расстояний и углов в пространстве.
Пространственные представления учащихся развиваются в процессе решения большого числа задач, требующих распознавания различных видов многогранников и форм их сечений, а также построения соответствующих чертежей.
Практическая направленность курса реализуется значительным количеством вычислительных задач.
Повторение и систематизация курса геометрии 10 класса – 8 часов.
Тематическое планирование
Алгебра
| № | Тема | Кол.часов | Дата провед. по плану | Фактич. дата провед. |
|
| Повторение и расширение сведений о функции | 16 |
|
|
| 1-3 | Наибольшее и наименьшее значение функции. Чётные и нечётные функции. | 3 |
|
|
| 4-5 | Построение графиков функций с помощью геометрических преобразований | 2 |
|
|
| 6-8 | Обратная функция | 3 |
|
|
| 9-11 | Равносильные уравнения и неравенства | 3 |
|
|
| 12-14 | Метод интервалов | 3 |
|
|
| 15 | Контрольная работа № 1 | 1 |
|
|
| 16 | Урок анализа контрольной работы | 1 |
|
|
|
| 2. Степенная функция | 25 |
|
|
| 17 | Степенная функция с натуральным показателем | 1 |
|
|
| 18-19 | Степенная функция с целым показателем | 2 |
|
|
| 19-20 | Определение корня n-й степени. Функция 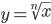 | 2 |
|
|
| 21-25 | Свойства корня n-й степени | 5 |
|
|
| 26- | Контрольная работа № 2 | 1 |
|
|
| 27-28 | Определение и свойства степени с рациональным показателем | 2 |
|
|
| 29-32 | Иррациональные уравнения | 4 |
|
|
| 33-36 | Метод равносильных преобразований для решения иррациональных уравнений | 4 |
|
|
| 37-39 | Иррациональные неравенства | 3 |
|
|
| 40 | Контрольная работа № 3 | 1 |
|
|
| 41 | Урок анализа контрольной работы | 1 |
|
|
|
| 3. Тригонометрические функции | 40 |
|
|
| 42-43 | Радианная мера угла | 2 |
|
|
| 44-46 | Тригонометрические функции числового аргумента | 3 |
|
|
| 47-48 | Знаки значений тригонометрических функций. Чётность и нечётность тригонометрических функций | 2 |
|
|
| 49 | Периодические функции | 1 |
|
|
| 50-52 | Свойства и графики функций 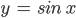 и и 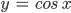 | 3 |
|
|
| 53-54 | Свойства и графики функций 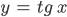 и и 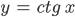 | 2 |
|
|
| 55 | Контрольная работа № 4 | 1 |
|
|
| 56 | Урок анализа контрольной работы | 1 |
|
|
| 57-61 | Основные соотношения между тригонометрическими функциями одного и того же аргумента | 5 |
|
|
| 62-65 | Формулы сложения | 4 |
|
|
| 66-68 | Формулы приведения | 3 |
|
|
| 69-73 | Формулы двойного и половинного углов | 5 |
|
|
| 74-76 | Сумма и разность синусов (косинусов) | 3 |
|
|
| 77-79 | Формулы преобразования произведения тригонометрических функций в сумму | 3 |
|
|
| 80 | Контрольная работа № 5 | 1 |
|
|
| 81 | Урок анализа контрольной работы | 1 |
|
|
|
| 4. Тригонометрические уравнения и неравенства | 30 |
|
|
| 82-85 | Уравнение 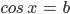 | 4 |
|
|
| 86-89 | Уравнение 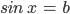 | 4 |
|
|
| 90-93 | Уравнения 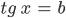 и и 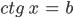 | 4 |
|
|
| 94-97 | Функции 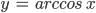 , , 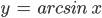 , , 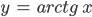 и и 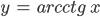
| 4 |
|
|
| 98-101 | Тригонометрические уравнения, сводящиеся к алгебраическим | 4 |
|
|
| 102-105 | Решение тригонометрических уравнений методом разложения на множители | 4 |
|
|
| 106-109 | Решение простейших тригонометрических неравенств | 4 |
|
|
| 110 | Контрольная работа № 6 | 1 |
|
|
| 111 | Урок анализа контрольной работы | 1 |
|
|
|
| 5. Производная и её применение | 40 |
|
|
| 112-114 | Представление о пределе функции в точке и о непрерывности функции в точке | 3 |
|
|
| 115-116 | Задачи о мгновенной скорости и касательной к графику функции | 2 |
|
|
| 117-119 | Понятие производной | 3 |
|
|
| 120-123 | Правила вычисления производных | 4 |
|
|
| 124-128 | Уравнение касательной | 5 |
|
|
| 129 | Контрольная работа № 7 | 1 |
|
|
| 130 | Урок анализа контрольной работы | 1 |
|
|
| 131-133 | Признаки возрастания и убывания функции | 3 |
|
|
| 134-137 | Точки экстремума функции | 4 |
|
|
| 138-143 | Применение производной при нахождении наибольшего и наименьшего значений функции | 6 |
|
|
| 144-150 | Построение графиков функций | 6 |
|
|
| 151 | Контрольная работа № 8 | 1 |
|
|
| 152 | Урок анализа контрольной работы | 1 |
|
|
|
| Повторение и систематизация учебного материала | 24 |
|
|
| 153-165 | Повторение и систематизация учебного материала за курс алгебры | 13 |
|
|
| 166-167 | Годовая контрольная работа | 2 |
|
|
| 168 | Урок анализа контрольной работы | 1 |
|
|
| 169-175 | Повторение. Решение задач. | 7 |
|
|
|
| Итог | 175 |
|
|
Геометрия
| № | тема | Кол. Часов по плану | Дата по плану | Фактическая дата проведения |
|
| Введение в стереометрию
| 6 |
|
|
| 1 | Основные понятия стереометрии. Аксиомы стереометрии. | 1 |
|
|
| 2-3 | Следствия из аксиом стереометрии | 2 |
|
|
| 4-6 | Пространственные фигуры. Начальные представления о многогранниках. Метод сечений. | 3 |
|
|
|
| Параллельность в пространстве
| 16 |
|
|
| 7-8 | Взаимное расположение прямых в пространстве | 2 |
|
|
| 9-11 | Параллельность прямой и плоскости | 3 |
|
|
| 12-14 | Параллельность плоскостей | 3 |
|
|
| 15-16 | Преобразование фигур в пространстве | 2 |
|
|
| 17 | Параллельное проектирование | 1 |
|
|
| 18-21 | Решение задач по теме параллельность в пространстве | 4 |
|
|
| 22 | Контрольная работа | 1 |
|
|
|
| Перпендикулярность в пространстве
| 20 |
|
|
| 23-24 | Угол между прямыми в пространстве | 2 |
|
|
| 25-26 | Перпендикулярность прямой и плоскости | 2 |
|
|
| 27-29 | Перпендикуляр и наклонная | 3 |
|
|
| 30-32 | Теорема о трех пепендикулярах | 3 |
|
|
| 33-34 | Угол между прямой и плоскостью | 2 |
|
|
| 35-36 | Двугранный угол. Угол между плоскостями | 2 |
|
|
| 37-38 | Перпендикулярность плоскостей | 2 |
|
|
| 39-41 | Площадь ортогональной проекции многоугольника | 3 |
|
|
| 42 | Контрольная работа | 1 |
|
|
|
| Многогранники | 18 |
|
|
| 43-45 | Многогранники. Призма | 3 |
|
|
| 46-48 | Параллелепипед | 3 |
|
|
| 49-52 | Пирамида | 4 |
|
|
| 53-55 | Усеченная пирамида | 3 |
|
|
| 56-59 | Решение задач | 4 |
|
|
| 60 | Контрольная работа | 1 |
|
|
|
|
|
|
|
|
| 61-70 | Обобщение и систематизация знаний учащихся.
| 10 |
|
|
Всего: 245 часов.







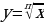 , выделяя случаи корней чётной и нечётной степени. Строить графики функций на основе графика функции
, выделяя случаи корней чётной и нечётной степени. Строить графики функций на основе графика функции 









