Равносильность систем

Дата 03.04.2020

Тема урока: РАВНОСИЛЬНОСТЬ СИСТЕМ.

Цели: обобщить и систематизировать знания учащихся о способах решения систем уравнений, рассмотреть основные утверждения о равносильности систем.

Ход урока

1. АКТУАЛИЗАЦИЯ ЗНАНИЙ

Прежде чем перейдем к изучению новой темы, давайте поработаем устно и немного подготовимся к ЕГЭ. Если не получается устно, то запишите решение в рабочую тетрадь. Помните, что на экзамене вы не будете пользоваться калькулятором, так что вычисляйте значения самостоятельно.

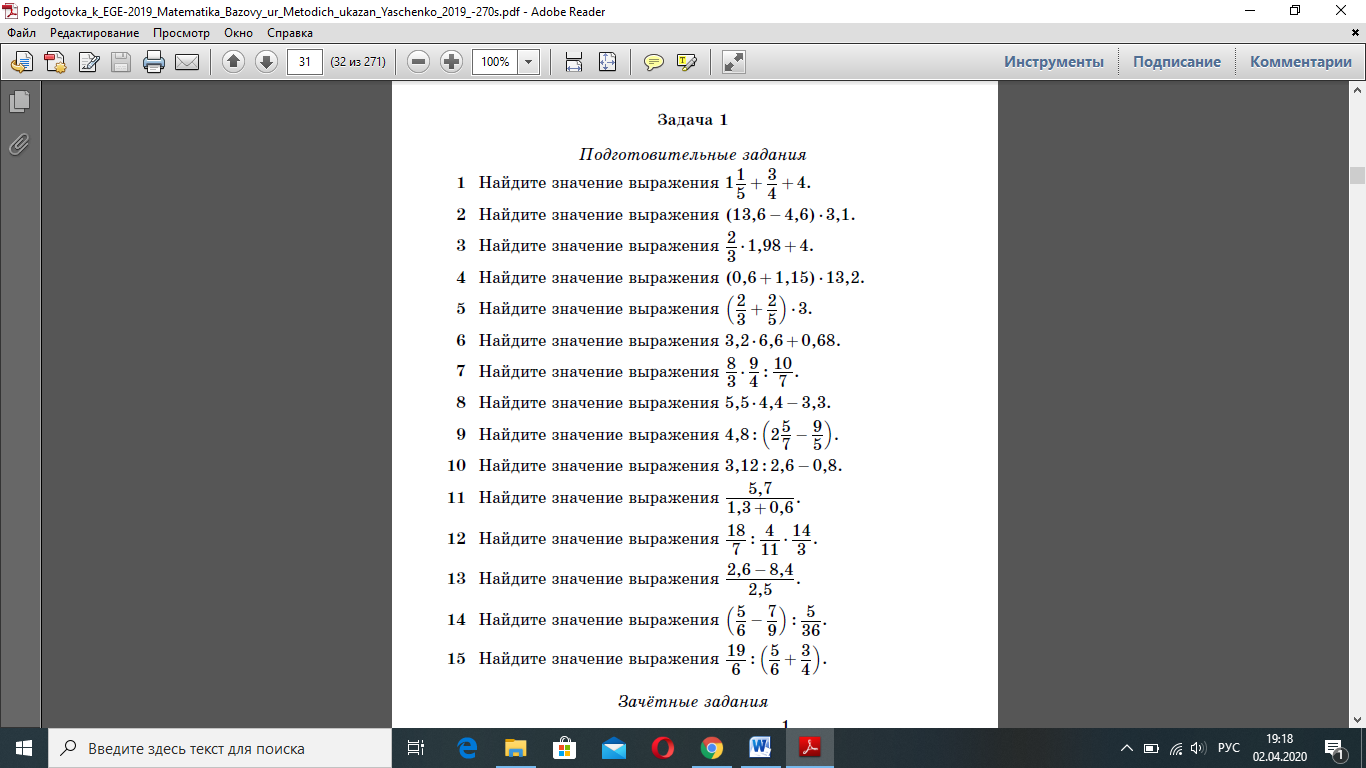
Ответьте устно на вопросы.

1. Что является решением системы двух уравнений с двумя неизвестными?

2. Что значит «решить систему уравнений»?

3. Какие уравнения называются равносильными? Можно ли это утверждать для систем?

4. Какие способы решения систем уравнений вы знаете?

1. ИЗУЧЕНИЕ НОВОГО МАТЕРИАЛА

Не смотря на тему сегодняшнего урока «Равносильность систем», по сути ничего нового мы сегодня не рассмотрим. Мы будем применять те же методы решения, что и раньше (метод подстановка, линейного преобразования), только уравнения, входящие в системы, усложняются различными функциями.

Откройте учебники и повторите известную нам теорию со стр. 331 по стр. 335.

Откройте тетради и запишите сегодняшнее число и тему урока. Все вместе запишем несколько примеров, а потом вы самостоятельно попытаетесь решить предложенные задачи в учебнике.

Пример 1. Решить систему уравнений

Решим данную систему способом подстановки. Выразим неизвестную у из первого уравнения и подставим во второе уравнение. Получим равносильную систему

Решим отдельно второе уравнение системы .

Вспомним формулу тригонометрии . Тогда преобразуем уравнение

.

Умножим его на 2, чтобы применить еще одну формулу из курса тригонометрии, получим

,

,

,

.

Далее возвращаемся к подстановке и находим значение у:

Ответ: ( ), .

Пример 2. Решить систему уравнений

Данную систему можно решить способом сложения. Первое уравнение не изменится, а вот второе получится путем сложения первого и второго уравнений. Получим равносильную ей систему:

Решим отдельно второе уравнение системы.

,

,

,

.

Теперь необходимо найти значение у. Подставим в первое уравнение системы х=3, получим:

,

,

,

,

.

Ответ: (3; 3).

Решим систему, требующую знаний прошлых уроков, а именно раскрытие модуля.

Пример 3. Решить систему уравнений:

Попробуем решить эту систему способом подстановки. Выразим х из второго уравнения . Но в первом уравнении у нас нет такого выражения. Попытаемся его получить. Перепишем систему в виде:

Теперь можем заметить подобные выражения, но они отличаются знаками. Продолжаем преобразовывать систему. Получим:

И выразим из второго уравнение выражение , получим равносильную систему:

Выполним подстановку в первое уравнение системы:

Рассмотрим отдельно первое уравнение системы. Теперь оно относительно одной неизвестной. Применяя свойства модуля перепишем это уравнение в виде

.

А далее вспоминайте тему «Решение уравнений с модулями». Раскроем модули по определению и получим следующую совокупность систем:

И будем решать каждую систему, тогда:

Дальше определяем принадлежат ли найденные корни каждой системы тем промежуткам, на которых раскрывались модули. Получим

Необходимо теперь найти значения у. Вспомним, что и решим уравнения

.

.

Ответ: ( ), ( ).

1. ПРАКТИЧЕСКАЯ ЧАСТЬ

Открываем учебники на странице 336 и выполняете самостоятельно следующие номера.

№14.10(а). В этой системе необходимо выразить у из второго уравнения и подставить в первое.

№14.14(а). Эта система быстро решается способом сложения, если первое уравнение системы умножить на 2.

1. ПОДВЕДЕНИЕ ИТОГОВ УРОКА. РЕФЛЕКСИЯ

Домашнее задание: №14.7(в), 14.8(а).