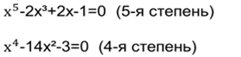Тема урока: «Линейные уравнения. Решение уравнений, сводящихся к линейным. Целое уравнение и его корни.»
Класс: 9
Цели: закрепить умения и навыки решения целых уравнений используя методы разложения многочлена на множители и введения новой переменной, использовать полученные знания для решения уравнений высших степеней; формирование умения применять накопленные знания для решения заданий в ОГЭ.
Планируемые результаты:
Предметные: научить в процессе реальной ситуации использовать определения следующих понятий: «корень уравнения», «степень уравнения», повторить способы решения уравнений первой и второй степени.
Личностные: приобретают навыки сотрудничества со взрослыми и сверстниками; установка на здоровый образ жизни, наличие мотивации к творческому труду, к работе на результат.
Метапредметные:
Регулятивные: умение обрабатывать информацию и ранжировать ее по указанным основаниям; формировать коммуникативную компетенцию учащихся; выбирать способы решения уравнений; контроль и оценка процесса и результатов деятельности.
Познавательные: овладение логическими действиями сравнения, анализа, синтеза.
Коммуникативные: готовность слушать собеседника и вести диалог; готовность признать возможность существования различных точек зрения и права каждого иметь свою; излагать своё мнение и аргументировать свою точку зрения.
Тип урока: комбинированный урок.
Формы работы: фронтальная, индивидуальная, работа в парах.
Методы обучения: словесный, наглядный, практический, проблемный.
Оборудование: классная доска, учебник, раздаточные материалы, ноутбук.
Ход урока:
Организационный момент. Мотивация учебной деятельности.
Мне бы хотелось, чтобы сегодня наш урок был полезен всем вам, и вы приобрели частицу мудрости.

Актуализация опорных знаний. Определение темы и цели урока.
Запись на доске.
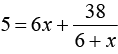
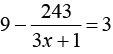
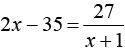

Х3 -8х2 –х +8=0 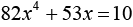
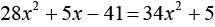

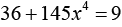 5х-7 = 4х=26 5х2 -4х-1=0
5х-7 = 4х=26 5х2 -4х-1=0
Устный опрос.
- Ребята что вы видите на доске? (Уравнения).
- Что такое уравнение? (Равенство, содержащее переменную)
-А что с уравнением обычно делают? (Решают)
- А что значит решить уравнение? (Найти все его корни, или доказать, что корней нет).
- Что называется корнем уравнения? (Значение переменной, при котором уравнение обращается в верное числовое равенство).
Разделите уравнения на две группы по виду выражений, из которых они состоят.
| Уравнения с целыми выражениями | Уравнения с дробными выражениями |
Как вы думаете, как будут называться уравнения в каждой группе? (Целые и дробные).
А мы умеем решать такие уравнения? А какие уравнения вы уже знаете и умеете решать? Какие они имеют степени?
Давайте решим эти уравнения и при этом вспомним какими способами решаются уравнения первой и второй степени. Как вы думаете, сколько корней могут иметь уравнения? От чего это зависит?
Итак, тема нашего урока: «Линейные уравнения. Решение уравнений, сводящихся к линейным. Целое уравнение и его корни.»
Давайте определим цели, которые мы поставим перед собой.
- Определять виды уравнений;
- учиться решать целые уравнения
Усвоение новых знаний.
Определение целого уравнения.
Уравнения, в которых левая и правая часть являются целыми выражениями, называются целыми уравнениями.
|
|  |
|
|
| 
|
| 
|
|
| 
| 
|
|  |  | 
| 
|
| 
|
| 1-й степени
(линейные) Р е ш е н и е: привести к виду ах = b х = 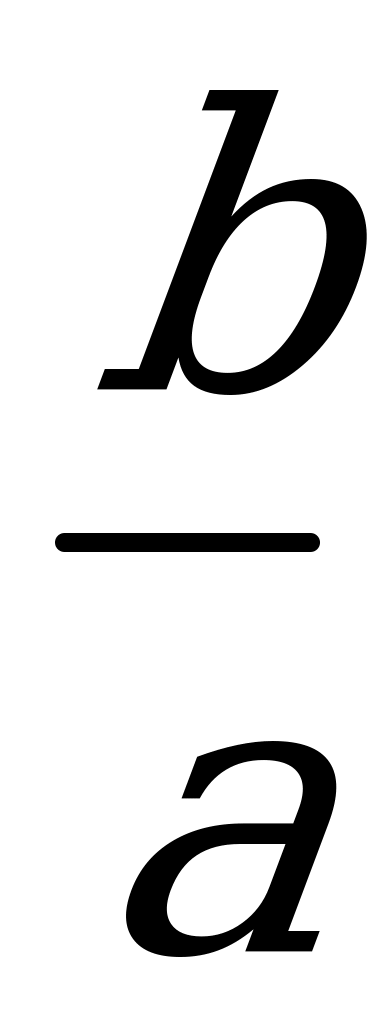 | 2-й степени (квадратные) Р е ш е н и е: D = b2 – 4ac x1, 2 = 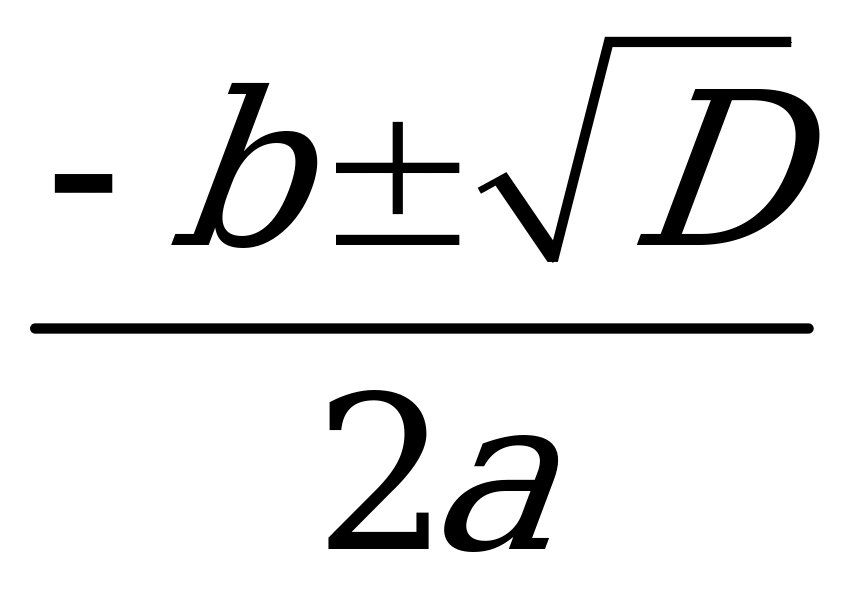 | Выше 2-й
степени | Решаемые по алгоритму |
| Решаемые методом замены |
|  
|
| Решаемые методом замены | Решаемые разложением
на множители |
|
|
2) Определите степень уравнения: Уравнения бывают 1, 2, 3, 4, и более высоких степеней. Мы с вами большей частью решаем уравнение I, II, III IV степени.
Всякое уравнение можно заменить равносильным ему уравнением, левая часть которого – многочлен стандартного вида, а правая – нуль.
Если уравнение с одной переменной записано в виде P(x) = 0, где P(x)- многочлен стандартного вида, то степень этого многочлена называют степенью данного уравнения
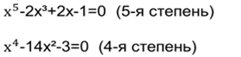
Всякое уравнение можно заменить равносильным ему уравнением, левая часть которого – многочлен стандартного вида, а правая – нуль.
Степенью произвольного целого уравнения называют степень равносильного ему уравнения вида Р(х)=0, где Р(х)- многочлен стандартного вида
x (x – 1) = 0 у² (у- 4) = 0
х² - х = 0 у3-4у² = 0
Закрепление понятия степени уравнения
Укажите степень уравнения (устно)
1) x2 = 0 6) x2 –16 = 0
2) x3 – 25x = 0 7) x4 – 3x2 = 0
3) 9x –27 = 0 8) x2 = – 49
4) 10 – х2 = 26х 9) x (x – 1) (x + 4) = 0
5) x (6 - x) (x - 9) = 0 10) (x2 – 25 ) х - x3 = 0
3) Примеры решения уравнений различных степеней:
1. Уравнение первой степени можно привести к виду ax+b=0, где х – переменная, a и b – некоторые числа, причём при a≠0. Из уравнения ax+b=0, при a≠0 получаем, что – корень уравнения. Каждое уравнение первой степени имеет один корень.
2х + 3 = 0
х = 4, х = - 3, х = 0 (являются ли корнями данного уравнения?)
2. Уравнения второй степени можно привести к виду ax2+bx+c=0, где х – переменная, a, b и c – некоторые числа, причём при a ≠ 0. Число корней такого уравнения зависит от дискриминанта D=b2–4ac
Решите уравнения:
I вариант II вариант III вариант (рассмотреть 2 способа решения x2-12x+36=(х-6)2)
x2-5x+6=0 y2-4y+7=0 x2-12x+36=0
D=1, D0, D=-12, D
x1=2, x2=3 нет корней x=6.
Сколько корней может иметь уравнение 2 степени (квадратное)? Не более двух!
3. Уравнение третьей степени можно привести к виду ax3+bx2+cx+d=0,
уравнение четвёртой степени – к виду ax4+bx3+cx2+dx+e=0, и т. д., где a, b, c, ... – некоторые числа, причём при a≠0
Динамическая пауза: гимнастика для глаз.

Уравнение n-ой степени может иметь не более n корней.
Мы знаем формулы, по которым решают линейные и квадратные уравнения. Для уравнений 3 и 4 степени также известны формулы корней, но они очень сложны и неудобны для практического применения. Что касается уравнений пятой и более высоких степеней, то общих формул корней не существует.
4. Первичное закрепление.
Выполняем № 265 (устно), 266 (а, б), 267 (а, б)
Подведение итогов урока. Рефлексия
Подведем итоги:
- Какое уравнение с одной переменной называется целым? Приведите пример.
- Как найти степень целого уравнения? Сколько корней имеет уравнение с одной переменной первой, второй степени?
-Уравнения каких степеней мы рассмотрели?
Притча:
Шел мудрец, а навстречу ему три человека, которые везли под горячим солнцем тележки с камнями для строительства. Мудрец остановился и задал каждому по вопросу. У первого спросил: «Что ты делал целый день?» И тот с ухмылкой ответил, что целый день возил проклятые камни. У второго мудрец спросил: «А что ты делал целый день?» и тот ответил: «А я добросовестно выполнял свою работу». А третий улыбнулся, его лицо засветилось радостью и удовольствием: «А я принимал участие в строительстве храма!»
Ребята! Давайте попробуем с вами оценить каждый свою работу за урок.
- Кто работал как первый человек?
- Кто работал добросовестно?
- Кто принимал участие в строительстве храма?
Домашнее задание:
Проработать п. 12, решить № 266 (в, г); №267 (а, б)