Линейные уравнения с параметрами

Линейные уравнения с параметрами

Работу подготовила:

ученица 7 А класса

МБОУ СОШ №2

Сердюкова Валерия

Актуальность данной темы определяется необходимостью уметь решать уравнения с параметрами при сдаче ЕГЭ.

Цель: научиться решать линейные уравнения с параметрами, используя различные способы.

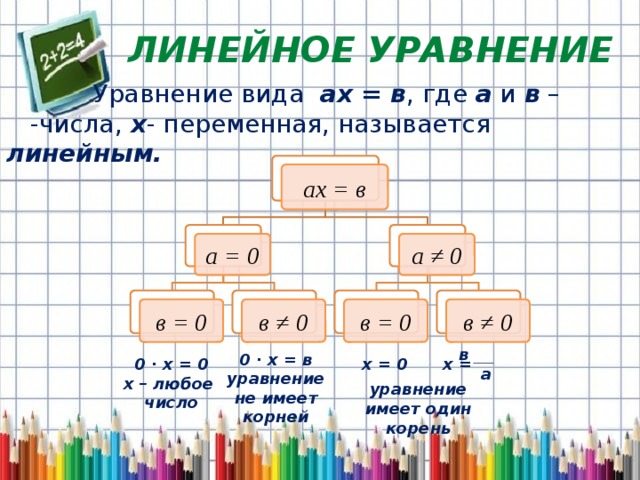
Линейное уравнение

Уравнение вида ах = в , где а и в – -числа, х - переменная, называется линейным.

ах = в

а = 0

а ≠ 0

в ≠ 0

в ≠ 0

в = 0

в = 0

в а

0 ∙ х = в

уравнение не имеет корней

0 ∙ х = 0

х = 0

х =

х – любое

число

уравнение имеет один корень

Параметр -это переменная величина, которая в процессе решения уравнения (задачи) считают фиксированной и относительно которой проводится анализ полученного решения.

Решить уравнение с параметром - это значит для каждого значения параметра найти значение неизвестной переменной, удовлетворяющее этому уравнению.

Существует два способа решения уравнений:

АНАЛИТИЧЕСКИЙ

и

Графический

Аналитический

ПРИМЕР 1: Решить уравнение относительно х:

х-3=а+8

ПРИМЕР 1: Решить уравнение относительно х:

х-3=а+8

Решение: х=а+11.

Переменную, которую надо найти, будем называть неизвестной , а переменную, через которую будем выражать искомую неизвестную, назовем параметром .

Заметим, что в нашем примере параметр а может принимать любые значения.

Ответ : при любом значении параметра а, х = а+5 .

Решение: х=а+11.

Переменную, которую надо найти, будем называть неизвестной , а переменную, через которую будем выражать искомую неизвестную, назовем параметром .

Заметим, что в нашем примере параметр а может принимать любые значения.

Ответ : при любом значении параметра а, х = а+11 .

ПРИМЕР 2: Решить уравнение относительно х:

(а + 4)х = 2а +1

Решение:

1)Если а + 4 = 0, т.е. а = - 4, то уравнение примет вид

0• х = -7 и не имеет решений;

2)Если а + 4 ≠ 0, т.е. а ≠ - 4, то уравнение примет вид

х = и имеет единственное решение.

Ответ: при а = - 4 нет решений; при а ≠ - 4 х = .

2а + 1

а + 4

2а + 1

а + 4

ПРИМЕР 3: Решить уравнение относительно х:

(а – 7)х = а(а – 7)

Решение:

1) Если а – 7 = 0, т.е. а = 7, то уравнение примет вид 0 •

х = 0 и имеет бесконечное множество решений

(х - любое число);

2) Если а – 7≠ 0, т.е. а ≠ 7, то уравнение примет вид

x = , х = а и имеет единственное решение.

Ответ: при a = 7 х - любое число; при а ≠ 7 х = а.

а(а – 7)

а - 7

ПРИМЕР 4: Решить уравнение относительно х:

(а – 7)х = – 14а + 49

Решение:

(а – 7)х = – 14а + 49

(а – 7)х =

1)Если а – 7 = 0, т.е. а = 7, то уравнение примет вид 0 •

х = 0 и имеет бесконечное множество решений (х - любое число);

2) Если а – 7 ≠ 0, т.е. а ≠ 7, то уравнение примет вид

(а – 7) 2

Ответ: при а = 7 х - любое число; при а ≠ 7 х = а – 7.

х =

,х = а – 7 и имеет единственное решение.

а - 7

ПРИМЕР 5: Решить уравнение относительно х:

- 1) х =

Решение:

- 1) х =

(а-1)(а+1) х = а + 1

1) Если а – 1 = 0, т.е. а = 1, то уравнение примет вид

0 • х =2 и не имеет решений ;

2) Если а + 1 = 0, т.е. а = -1, то уравнение примет вид

0 • х = 0 и имеет бесконечное множество решений (х - любое число);

3) Если а ≠ 1, х = и имеет единственное решение.

Ответ: при а = 1 решений нет, при а = - 1 х - любое число;

при а ≠ 1 х = .

1

+

-

а - 1

1

+

-

а - 1

Графический

х-3=а+8

(а + 4)х = 2а +1

(а – 7)х = а(а – 7)

(а – 7)х = – 14а + 49

- 1) х =

Значение параметра а