Математическая грамотность. 5 класс.

Компетентностные задачи по математике.

Компетентностный подход в школе помогает научиться ученикам самостоятельно действовать в ситуациях неопределенности в решении актуальных проблем. Для реализации компетентностного подхода в обучении необходимо регулярно задавать ученикам вопросы:

- «Где в жизни вам пригодятся эти знания и умения?»;

- систематически включать в урок компетентностные задачи или задания на применение предметных знаний для решения практической задачи, а также задачи на ориентацию в жизненной ситуации.

Практические задачи или задачи, связанные с повседневной жизнью.

Задача № 1

Витя вылепил игрушку из глины за 40 мин. На раскрашивание этой игрушки он потратил времени в 2 раза меньше, а потом в течение 1 ч игрушка обжигалась в печи. Сколько времени ушло на изготовление игрушки?

Решение:

1ч=60мин.

Составим схему.

При решении задачи дети карандашом вписывают в пустые квадратики найденные данные.

1. 40:2=20(мин.)- ушло на раскрашивание.

2. 40+20+60=120(мин)- ушло на изготовление игрушки.

3. 120мин.=2ч

Ответ: 2 часа.

Задача № 2

В шкафу было 16 чашек с синими цветочками, чашек в горошек – на 2 меньше, чайных ложек – на 12 больше, чем чашек в горошек. Сколько одновременно человек смогут пить чай, если у каждого должна быть своя чашка и своя чайная ложка?

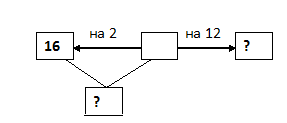
Решение:

1) 16-2=14 (шт.)- чашек в горошек.

2) 14+12=26 (шт.) – чайных ложек.

3) 16+14=30(шт.) – чашек всего.

Ответ: так как ложек 26, а чашек 30 значит, пить чай смогут 26 человек.

Задача № 3

Длина коридора 36 м. Есть три куска линолеума: первый кусок длиной 12м, второй – в 2 раза короче, а третий – на 2 м короче первого. Хватит ли их, чтобы покрыть пол в коридоре (ширина кусков и ширина коридора совпадают)?

Решение:

1) 12:2=6(м)- длина второго куска.

2) 12-2=10(м)- длина третьего куска.

3) 12+6+10=28(м) – всего линолеума.

Ответ: так как длина коридора 36 м, линолеума 28м, значит, 36-28= 8 м не хватает.

Задача № 4

Коля весит 45кг, Дима – на 7 кг меньше, а Вася – на 5кг больше Димы. Смогут ли эти ребята подняться одновременно на лифте, если этот лифт за один раз поднимает не больше 120 кг.

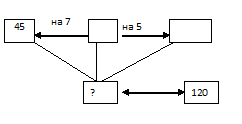
Решение:

1) 45-7=38(кг)-весит Дима.

2) 38+5=43(кг) – весит Вася.

3) 45+38+43=126(кг) – вес троих ребят.

Ответ: лифт за один раз поднимает не больше 120 кг, а вес ребят 126 кг. Эти ребята не смогут подняться одновременно.

Задача № 5

В парнике выращивали помидоры, причём часть из них отправляли на продажу, а остальное оставляли на семена. Сколько килограммов помидоров оставили на семена, если в магазин каждую неделю отправляли по72 кг помидоров, а всего за месяц собрали 300кг помидоров?

Решение:

1. 72*4=288(кг) - отправили в магазин за месяц

2. 300-288=12(кг) - оставили на семена.

Ответ: 12 кг.

Задача № 6

Носильщику необходимо доставить на горную базу 225кг груза. В каждую свою ходку он несёт полный рюкзак весом 50кг, а на него сверху крепит коробку с грузом в 2 раза меньше. Сколько ходок надо сделать носильщику, чтобы доставить весь груз на базу?

Решение:

1. 50:2=25(кг)- весит груз.

2. 50+25=75 (кг) – несет за одну ходку.

3. 225:75=3(х) – потребуется для всего груза.

Ответ: 3 ходки.

Задача № 7

На прямоугольном участке длиной 40м и шириной 30м посадили свёклу. С каждых 100 собрали по 4 ц свёклы. Весь урожай разложили в мешки по 16 кг в каждый. Сколько мешков для этого потребовалось?

Решение:

1. 40*30=1200( )- площадь участка.

2. 1200:100=12 (шт) – количество участков, с которых собирали по 4 ц.

3) 4*12=48 (ц)- собрали со всего участка.

4) 48:16=3(м)- потребовалось для 48ц.

Ответ: 3 мешка.

Задача № 8

Парикмахер за день постриг 5 человек, затратив на каждого по 30 мин, и трём женщинам он сделал праздничную причёску, затратив на каждую по 1ч 15 мин, ещё 30 мин у него ушло на обеденный перерыв. Сколько времени показывали часы, когда парикмахер освободился. Если его рабочий день начался в 8ч 30 мин?

Решение:

1. 30*5=150(мин) – ушло на 5 стрижек.

2. 150мин=2ч 30 мин

3. 1ч15мин*3=3ч 45мин – ушло на 3 праздничных причёски.

4. 2ч 30мин+ 3ч 45мин + 30мин = 6ч 45 мин – парикмахер был на работе.

5. 8ч 30 мин + 6ч 45мин= 15ч 15 мин – показывали часы, когда парикмахер освободился.

Ответ: 15ч 15 мин

Задача № 9

Для каждого ученика класса купили учебник по математике и учебник по русскому языку. Учебник по математике стоил 450р., а учебник по русскому языку – 550 р. За всю покупку заплатили 28000р. Сколько стоили все учебники по математике и все учебники по русскому языку?

Решение:

1. 450+550=1000 (р.)- цена 1 комплекта.

2. 28000:1000=28 (шт)- количество комплектов.

3. 450*28=12600 (р.) – стоимость учебников по математике.

4. 28000-12600= 15400 (р.) – стоимость учебников по русскому языку.

Задача № 10

В магазине «Кулинария» в холодильник загрузили 6 коробок с пирожными по 8 пирожных в каждой коробке и столько же коробок по 5 пирожных в каждой. Сколько пирожных осталось, если было продано52 пирожных.

Решение:

1. 8*6=48(шт.) - в больших коробках.

2. 5*6=30 (шт.) - в меньших коробках.

3. 48+30=78 (шт.) - всего.

4. 78-52=26(шт.) - осталось.

Ответ: 28штук.

Задача № 11

Для оформления зала привезли 12 упаковок по 25 круглых воздушных шариков и несколько упаковок по 18 фигурных воздушных шариков. Когда уже надули 397 шариков, осталось надуть 65 шариков. Сколько привезли упаковок фигурных шариков?

Решение:

1. 397+65=462(шт.) – всего.

2. 25*12=300(шт.) – круглых шариков.

3. 462-300=162 (шт.)- фигурных шариков .

4. 162:18=9 (уп.) -фигурных шариков.

Ответ:9 упаковок.

Задача № 12

На 30 самолетах Ту-134 можно перевести 2700 пассажиров. В пяти самолётах Ту-134 помещается столько пассажиров, сколько в трёх самолётах Ту- 154. Сколько пассажиров можно перевести на самолёте Ту – 154?

Решение:

1. 2700:30=90 (ч.) – в 1 самолете Ту-134.

2. 90*5=450(ч.) – в 5 самолётах Ту- 134.

3. 450:3=150 (ч.) – в 1 самолёту Ту -154.

Ответ: 150 человек.

Задача № 13

В кинотеатре 4 зала: 2 зала по 120 мест и 2 зала по 150 мест. После начала сеанса в кассе осталось 22 билета. Сколько билетов было продано?

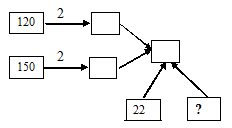
Решение:

1. 120*2=240 (м.) - в двух меньших залах.

2. 150*2=300 (м.) – в двух больших залах.

3. 240+300=540 (м.) – всего.

4. 540-22=518 (б.) – продано.

Ответ: 518 билетов.

Задача №14

Друзья решили сделать подарок Наташе ко дню рождения. Для этого они собрали деньги: пять из них дали по 70р, а остальные трое – по 90 р. Этих денег как раз хватило, чтобы купить куклу за 430 р. и букет цветов. Сколько стоит букет цветов?

Решение:

1. 70*5+90*3=620(р) – собрали всего.

2. 620-430=190 (р) – стоит букет.

Ответ: 190 рублей.

Задача № 15

В зале 65 мест в партере, 10 лож в амфитеатре по 6 мест каждая и ещё 100 мест в бельэтаже. На спектакль пришли 192 человека. Сколько мест осталось свободными?

Решение:

1. 6*10=60 (м.) – в 10 ложах.

2. 60+65+100=225 (м.) – всего.

3. 225-192=33(м.) – осталось.

Ответ: 33места.

Задача № 16

На фабрике ёлочные игрушки укладывали в коробки по 4шт. в каждую. Коробки упаковывали в ящики по 12 в каждый, а ящики – в контейнеры по 45 в каждый. Сколько ёлочных игрушек потребовалось для 7 таких контейнеров?

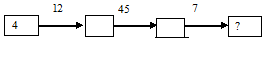
Решение:

1. 4*12=48(игр.) – в 1 ящике.

2. 48*45=2160 (игр.) – в 1 контейнере.

3. 2160*7=15120 (игр.) – в 7 контейнерах.

Ответ: 15120 игрушек.

Задача № 17

Печенье упаковали в пачки по 250 г. Пачки сложили в ящик в 4 слоя. Каждый слой имеет 5 рядов по 6 пачек в каждом. Выдержит ли ящик, если максимальная масса, на которую он рассчитан, равна 32 кг?

Решение:

1) 6*5=30 (пачек)- в 1 слое

2) 30 * 4=120(пачек) -всего в ящике

3) 120*250=30000 (г)=30 (кг)- масса всего печенья, что меньше максимальной массы, на которую рассчитан ящик.

Ответ: ящик выдержит.

Задача № 18

Настя пришла в школьную столовую пообедать, у неё с собой есть 90 рублей. В столовой висит меню:

Первые блюда	Свекольник	25 рублей
	Суп куриный	32 рублей
Вторые блюда	Котлета куриная с макаронами	55 рублей
	Овощное рагу	40 рублей
	Плов	58 рублей
Напитки	Компот	12 рублей
	Морс	15 рублей

Выбери обед из трёх блюд (первое, второе и напиток), который может купить Настя. В ответе укажи названия блюд и стоимость обеда.

Задача № 19

Определи стоимость приготовления салата «Оливье», если для этого требуется:

Картофель-250 грамм

Зелёный горошек- 1 банка

Яйца- 5 штук

Маринованные огурцы – 1 банка

Майонез- 1 пакет

Филе курицы-500 грамм

Яйца стоят 70 рублей за 10 штук, 1кг картофеля-60 рублей, пакет майонеза – 62 рубля, банка зелёного горошка – 57 рублей, банка маринованных огурцов – 87 рублей, 1 кг филе курицы – 140 рублей.

Решение:

1)250 г – это 4 часть килограмма, тогда 60:4=15(руб)-стоит картофель

2) 5штук яиц это половина, тогда 70:2= 35 (руб)

3)500 грамм это половина килограмма 140:2=70 (руб) –стоит филе курицы.

3)15+57+35+87+62+70=326 рублей.

Ответ: 326 рублей

Задача № 20

Определи стоимость приготовления 1 кг салата «Греческий», если для этого требуется:

Помидоры – 4 штуки

Огурец-3 штуки

Перец – 2 штуки

Маслины-1 банка

Сыр -1 упаковка

Листья салата-1 упаковка

Помидоры стоят 11 рублей за штуку, банка маслин стоит 52 рубля, огурцы – 8 рублей за штуку, упаковка сыра стоит 89 рублей, перец-24 рубля за штуку, упаковка листьев салата стоит 35 рублей.

Решение:

1. 11*4= 44 (руб)-стоят помидоры.

2. 8*3=24(руб)- заплатят за огурцы

3. 24*2=48 (руб)-заплатят за перец.

4. 44+24+48+52+89+35=292 (руб)

Ответ: 292 рубля.

Задача № 21

Длительность каждой серии некоторого телесериала равна 20 минутам. Сколько времени составляет длительность всего сериала, если его показывали ежедневно с 14 января по 5 февраля по две серии в день (в январе 31 день). Ответ вырази в часах и минутах.

Решение:

1. С 14 января по 5 февраля сериал шёл 23 дня.

2. 20*2=40(мин) – в день идёт сериал.

3. 23*40=920 (мин) - за 23 дня.

4. 1ч-60 мин, тогда 920:60=15ч 20 мин – длится весь сериал.

Ответ:15 часов 20 минут.

Задача № 22

В футболе команда получает за победу 3 очка, за ничью – 1 очко, за поражение – 0 очков. Команда сыграла в чемпионате страны 30 матчей и набрала 75 очков. Какое наибольшее число ничейных матчей могло быть у этой команды?

Решение:

1. 30*3=90(очков)- допустим, набрала за победу.

2. 90-75=15 (очков)- за ничью.

3. 75-15=60 (очков) - за победу.

Ответ: 15 очков – это наибольшее число ничейных матчей могло быть у этой команды.

Задача №23

На катке катались девочки и мальчики: девочек было в 2 раза больше, чем мальчиков, а мальчиков – 16. Через некоторое время 12 ребят ушли домой, но пришли ещё 8 девочек и 9 мальчиков. Сколько всего ребят стало на катке?

Мальчики 12 Девочки

9 8

16 ?,в 2р.Б

?

1. 16*2=32(чел.) – девочки.

2. 32+16=48 (чел) – всего.

3. 48-12=36(чел) – осталось.

4. 9+8=17(чел) – пришло.

5. 36+17=53(чел) – стало.

Ответ: 53 ребят стало на катке.

Задача № 24

Врачи рекомендуют в первый день отдыха на море незагоревшему человеку проводить на солнце 20 мин, а потом каждый день можно увеличивать время пребывания на солнце на 5 мин. Лена начала загорать в понедельник. Сколько времени она может находиться на солнце в ближайшее воскресенье?

Решение:

1. 5*6=30(мин)- на столько можно увеличить время пребывания на солнце за 6 дней.

2. 20+30=50 (мин)- может находиться на солнце в ближайшее воскресенье.

Ответ: 50 минут.

Задача № 25

Двум бригадам маляров было поручено покрасить забор вокруг дачного посёлка. Длина забора – 6 км, высота – 2 м. В одной бригаде – 3 человека, в другой – 5 человек. Сколько квадратных метров придётся на каждого маляра, если распределить работу равномерно?

Решение:

1. 6 км=6000м

2. 6000*2=12000 ( ) – площадь забора.

3. 3+5=8(ч)- в двух бригадах.

4. 12000:8=1500( )- на каждого маляра.

Ответ: 1500

Задача №26

Большой бидон с молоком весит 34 кг. После того как половину молока отлили, бидон стал весить 18кг 500г. Сколько весит пустой бидон?

Решение:

1. 34кг-18кг 500г=15кг 500г - отлили (это половина молока)

2. 18кг500г-15кг500г=3кг - весит пустой бидон.

Ответ: 3 кг.

Задача №27

В автобусе ехало 16 пассажиров, на первой остановке вышло 3 пассажира и зашло 7 человек. На второй остановке вышло 9 человек, а зашло 8 человек. Сколько человек стало в автобусе?

Решение:

1. 16-3+7=20 (ч.)- после первой остановки.

2. 20-9+8=19 (ч.)- стало.

Ответ: 20 человек.

Задача № 28

Мальчик ехал в школу на велосипеде. Занятия в школе начинаются в 9 ч. В 8 ч 40 мин он проехал половину пути, а в школу приехал за 10 мин до начала занятий. Сколько минут мальчик ехал в школу?

Решение:

1)8ч.50м.- 8ч.40м.=10 (мин.) проехал он половину пути 8ч50мин.

2) 8ч40мин = 10 мин — это половина пути.

3)10м * 2=20 (мин.) -весь путь.

Ответ: 20 минут мальчик ехал в школу.

Задача № 29

Счётчик автомобиля показывал 12921 км. Через 2 часа на счётчике снова появилось число, которое читалось одинаково в обоих направлениях. С какой скоростью ехал автомобиль?

Решение:

Ближайшее "двустороннее число"- 13031.
1)13031-12921=110( км) – за два часа.
2)110:2=55( км/ч)- скорость автомобиля.

Ответ: 55 км/ч

Задача №30

Если для ремонта покупать краску в банках по 600г в каждой, то потребуется 15 банок, причём 500 г краски оcтанется неиспользованной. Сколько надо купить банок по 800 г краски в каждой?

Решение:

1)600 * 15= 9000(г)-краски всего.
2)9000-500= 8500(г)- использованной краски.
3)8500:800=10(б.)625(г) =11 - банок нужно.

Ответ: 11 банок краски нужно купить.

Задача №31

Двум ученикам надо умножить одно и то же число: первому на 132, второму на 264. Первый получил в произведении 14388. Какое произведение должен получить второй ученик?

Решение:

1)14388:132=109 - базовое число.
2) 109*264=28776
Ответ: 28776 получится у второго ученика.

Задача №32

В выставочном зале прямоугольной формы надо настелить линолеум. Длина зала 24 м и ширина 16 м. В каждом рулоне 12 м линолеума шириной 1600 см. Сколько потребуется рулонов?

Решение:

Длина зала-24 м
Ширина зала-16м
Длина рулона 12 м
Ширина рулона-1600см ,для удобства см переводим в метры, так 1600см=16м.
Рулонов на весь зал-?
1)24*16=384(кв.м) - площадь зала
2)12*16=192 (кв.м)- площадь 1 рулона линолеума.
3)192+192=384 - значит необходимо два таких рулона
Ответ: потребуется 2 рулона линолеума.

Нестандартные задачи.

Наибольшие затруднения у школьников, как правило, вызывают решения нестандартных задач, т.е. задач, алгоритм решения которых им неизвестен. Однако одна и та же задача может быть стандартной или нестандартной в зависимости от того, обучал ли учитель решению аналогичных задач учащихся, или нет. Умение мыслить логически, выполнять умозаключения без наглядной опоры, сопоставлять суждения по определенным правилам- необходимое условие усвоения учебного материала на уроках математики в начальных классах.

1.У него есть четыре, но если их все отрезать, то у него станет целых восемь. О чем идет речь? Об углах четырехугольника

2.Если в 12 часов ночи идет дождь, то можно ли ожидать, что через 72 часа будет солнечная погода?

Нет, так как через 72 часа снова будет полночь.

3.В парке 8 скамеек. Три покрасили. Сколько скамеек стало в парке?

Восемь.

4. Термометр показывает плюс 15 градусов. Сколько градусов покажут два таких термометра? 15 градусов.

5.Батон разрезали на три части. Сколько сделали разрезов? Два разреза.

6.Что легче 1 кг ваты или 1 кг железа? Одинаково.

7.Грузовик ехал в деревню. По дороге он встретил 4 легковые машины. Сколько машин ехало в деревню? Одна.

8.В 9-этажном доме есть лифт. На первом этаже живет 2 человека, на втором 4 человека, на третьем 8 человек, на четвертом 16, на пятом 32 и так далее. Какая кнопка в лифте этого дома нажимается чаще других?

Кнопка первого этажа.

9.На дереве сидели 7 воробьёв, одного из них съела кошка. Сколько воробьёв осталось на дереве?

Ни одного: оставшиеся в живых воробьи разлетелись.

10. К тебе пришли гости, а в холодильнике бутылка лимонада, пакет с яблочным соком и бутылка минеральной воды. Что ты откроешь в первую очередь?

Холодильник.

11.Сколько концов у трех палок? У четырех с половиной? у двух с четвертью?

У трех – 6, у четырех с половиной – 10, у двух с четвертью – 6.

12.В светильнике было 20 лампочек, 5 из них перегорели. Сколько лампочек осталось?

Двадцать лампочек (15 работающих и 5 перегоревших).

13. Папа на рыбалке за 10 минут поймал 3-х рыбок. За какое время он поймает еще 10 рыбок?

Задача не имеет однозначного ответа.

14.На подносе лежали 9 булочек. 9 девочек взяли по булочке. Но на подносе осталась одна булочка. Как такое получилось?

Последняя девочка взяла булочку вместе с подносом.

15.Васе 5 лет. А Ане 9 лет. Какая разница в возрасте будет между ними через три года?

Четыре года (разница с возрастом не меняется).

16.Из леса Миша принес бабушке для грибного супа  2 белых гриба, 3 подосиновика, 4 мухомора и 5 сыроежек. Сколько грибов пригодится бабушке на суп?

10 грибов, мухомор – несъедобный гриб.

17.В подъезд одновременно зашли два человека. У одного квартира на 3-м этаже, у другого – на 9-м. Во сколько раз первый доедет быстрее 2-го?

В 4 раза,т.к.1-му надо преодолеть 2 промежутка между этажами, а 2-му – 8.

18.Верблюд в течение часа выдерживает ношу в 10 пудов. В течение какого времени он выдержит ношу в 1000 пудов?

Никакого. Верблюд не выдержит такой вес

18.Собрались как-то ребята на пикнике, всего 6 человек. Смотрят, а вместо 6 яблок они взяли 5. Как разделить яблоки поровну между всеми, чтоб никому не было обидно? Ни резать, ни ломать их нельзя.

Нужно сварить из яблок компот.

19.Врач прописал больному три таблетки и велел принимать их через каждые полчаса. Сколько времени уйдет на прием таблеток?

На первый взгляд может показаться, что человек выпьет последнюю таблетку через полтора часа, ведь это именно три раза по полчаса. На самом же деле он выпьет последнюю таблетку не через полтора часа, а через час. Человек сразу же выпевает первую таблетку. Проходит полчаса. Он выпевает вторую таблетку. Проходит ещё полчаса. Он выпивает третью таблетку. Стало быть, человек выпьет последнюю таблетку через час после начала лечения

20.На руках десять пальцев. Сколько пальцев на десяти руках? Пятьдесят.

21.Как разделить пять яблок между пятью людьми таким образом, чтобы одно яблоко осталось лежать в корзине? (Задача-шутка)

Один из пяти человек должен забрать свое яблоко вместе с корзиной. Эффект этой не очень серьезной задачи основан на двусмысленности выражения «яблоко осталось лежать в корзине». Ведь его можно понимать и в том смысле, что оно никому не досталось, и в том, что оно просто не покидало место своего первоначального пребывания, а это совершенно разные вещи. 22. Как число 66 увеличить в полтора раза, не производя над ним никаких арифметических действий?

Число 66 надо всего лишь перевернуть «вверх ногами». Получится 99, а это и есть 66, увеличенное в полтора раза.

23.В пруду растет один лист лилии. Каждый день число листьев удваивается. На какой день пруд будет покрыт листьями лилии наполовину, если известно, что полностью он будет покрыт ими через 100 дней?

Пруд будет покрыт листьями лилии наполовину на 99-й день. По условию число листьев каждый день удваивается, и если на 99-й день пруд покрыт листьями наполовину, то на следующий день и вторая половина пруда будет покрыта листьями лилии, т.е. полностью пруд покроется ими через 100 дней.

24.Если три дня назад был день, предшествующий понедельнику, то какой день будет послезавтра?

Перед понедельником было воскресенье. Если три дня назад было воскресенье, то сегодня — среда. Если сегодня — среда, значит, послезавтра будет пятница

25.Сколько у вас было всего прапрадедушек и прапрабабушек?

У каждого человека 2 родителя, 4 бабушки и дедушки, 8 прабабушек и прадедушек.

26.Катя живёт на четвёртом этаже, а Оля – на втором. Поднимаясь на четвёртый этаж, Катя преодолевает 60 ступенек. Сколько ступенек надо пройти Оле, чтобы подняться на второй этаж?

На первый взгляд может показаться, что Оля проходит 30 ступенек – в два раза меньше, чем Катя, так как она живёт в два раза ниже её. На самом деле это не так. Когда Катя поднимается на четвёртый этаж, она преодолевает 3 лестничных пролёта между этажами. Значит между двумя этажами 20 ступенек: 60 : 3 = 20. Оля поднимается с первого этажа на второй, следовательно, она преодолевает 20 ступенек.

27.Каким образом из кружки, ковшика, кастрюли и любой другой посуды правильной цилиндрической формы, наполненной до краёв водой, отлить ровно половину, не используя никаких измерительных приборов?

Любая посуда правильной цилиндрической формы, если смотреть на неё сбоку, представляет собой прямоугольник. Как известно, диагональ прямоугольника делит его на две равные части. Точно так же цилиндр делится пополам эллипсом. Из наполненной водой посуды цилиндрической формы надо отливать воду до тех пор, пока поверхность воды с одной стороны не достигнет угла посуды, где её дно смыкается со стенкой, а с другой стороны края посуды, через который она выливается. В этом случае в посуде останется ровно половина воды.

28.Три курицы несут три яйца за три дня. Сколько яиц снесут 12 куриц за 12 дней?

Можно сходу ответить, что 12 куриц за 12 дней снесут 12 яиц. Однако это не так. Если три курицы за три дня несут три яйца, значит одна курица за те же три дня несёт одно яйцо. Следовательно, за 12 дней она снесёт: 12 : 3 = 4 яйца. Если же куриц будет 12, то за 12 дней они снесут: 12 · 4 = 48 яиц.

29.Половина от половины числа равна половине. Какое это число?

Это число 2. Половина этого числа равна 1, а половина от половины этого числа (т. е. единицы) равна 0,5, т. е. тоже половине.

30.Попугай прожил меньше 100 лет и умеет отвечать только на вопросы «да» и «нет». Сколько вопросов ему надо задать, чтобы узнать его возраст?

На первый взгляд может показаться, что попугаю можно задать до 99 вопросов. На самом же деле можно обойтись гораздо меньшим числом вопросов. Спросим его так: «Тебе больше 50 лет?» Если он ответит «да», то его возраст от 51 до 99 лет; если же он ответит «нет», то ему от 1 года до 50 лет. Количество вариантов его возраста после первого же вопроса сокращается вдвое. Следующий подобный вопрос: «Тебе больше (можно спросить – меньше) 25 лет?», «Тебе больше (меньше) 75 лет?» (в зависимости от ответа на первый вопрос) сокращает число вариантов в четыре раза и т. д. В итоге попугаю надо задать всего 7 вопросов.

31.Семеро шли – семь рублей нашли. Если бы не семеро, а трое пошли, то много бы нашли? (Задача-шутка.)

Если бы не семеро, а трое пошли, то всё равно те же самые семь рублей и нашли.

32.Сережа поднимается по лестнице. Каждый раз он перепрыгивает через одну ступеньку. Сейчас он - на третьей ступеньке. На какой ступеньке он окажется, сделав три своих «шага»? (9)

33.Автобусу нужно 30 минут, чтобы добраться из пункта А в пункт Б.
Автобусы из пункта А отправляются каждые две минуты.

Одновременно с одним из автобусов из пункта А в пункт Б отправился автомобиль. Автомобилю требуется 7,5 минут, чтобы добраться до пункта Б. Сколько автобусов обгонит на своем пути автомобиль? (12)

34.На Новый Год школьники украшали ёлку. Ребятам раздали 62 елочных игрушек таким образом, чтобы каждый ученик получил хотя бы по одной игрушке и ни у кого из двух школьников не было поровну новогодних украшений. Сколько учеников участвовало в украшении елки?

РЕШЕНИЕ: Тут удобнее нарисовать схему и по ней распределить все 62 ёлочных украшения. Сразу станет видно, что согласно условию игрушки распределятся так: 1 ученику - 1 игрушка, 2 ученику – 2 елочных игрушки, 3 учащемуся – 3 игрушки … 11-му школьнику достанется 7 последних ёлочных игрушек: 62 - 55 = 7
Но по условию задачи у нас уже есть один учащийся (7-ой по счету), который тоже имеет 7 игрушек - т.е. последней 11-ый уже не участвует в украшении елки
ОТВЕТ: 10 учеников участвовало в украшении школьной ёлки

35.У Максима и Никиты вместе 240 фишек. Максим подарил Никите 40 фишек. У них стало фишек поровну. Сколько фишек было у каждого мальчика до этого?

РЕШЕНИЕ:
У Максима и Никиты на двоих 240 фишек. Считаем: 240:2=120.
Максим подарил 40 фишек Никите. Считаем: 120-40=80.
После этого у них стало поровну фишек. Считаем: 80+40=120.
Сколько у Максима было фишек, прежде чем он подарил Никите 40 фишек. Считаем: 120+40=160.
Сколько было у Никиты до того, как ему подарили 40 фишек. Решение: 120-40=80. Получается, что у Максима было 160 фишек, а у Никиты - 80.
ОТВЕТ: у Максима было 160 фишек, а у Никиты - 80.

36.Вера съела вдвое меньше Светы. Витя съел вдвое меньше, чем Вера. Сколько мороженого съел каждый, если всего они съели 21 порцию мороженого?
РЕШЕНИЕ: Вера съела на три больше, чем Витя и вдвое меньше Светы.
Решаем задачу подбором.
Допустим, что Вера съела 6 порций мороженого. Витя на три меньше. Решение: 6-3=3.
Света съела вдвое больше Веры. Решение: 6х2=12.
Витя съел 3 порций мороженого, Вера - 6, Света - 12.
ОТВЕТ: Витя съел 3 порции мороженного, Вера - 6, а Света 12 порций.

37.В кукольном театре в одном ряду сидит семья из четырёх человек: папа, мама, дочь, сын. Если дочь, сидящая последней справа, сядет между папой и мамой, то папа окажется последним справа. Кто где сидит? РЕШЕНИЕ: Известно, что дочь сидит последней справа, то слева от неё сидят папа, мама, сын. Если она сядет между мамой и папой, тогда папа будет последним справа. Получается мама с папой к ней сидят ближе, чем её брат. Папа сидит ближе всех, потому что если дочь сядет между родителями, то папа окажется последним справа. Выходит, что они сидят, начиная слева: сын, мама, папа и дочь. Для облегчения решения задачи можно нарисовать рисунок либо схему.

38.Незнайка заметил, что яйцо всмятку сварилось за 3 минуты. Тогда он решил, что 2 яйца будут вариться вдвое дольше, то есть 6 минут. Прав ли Незнайка? РЕШЕНИЕ: Незнайка не прав, потому что яйца будут вариться вместе, то есть вариться за 3 минуты. Количество яиц не имеет значения. Одно яйцо варится 3 минуты, 2 яйца тоже будут вариться 3 минуты. ОТВЕТ: 2 яйца будут вариться 3 минуты.

39.Лена и Света сорвали 40 яблок. Когда они съели поровну яблок, то у Лены осталось 15 яблок, а у Светы 9 яблок. Сколько яблок сорвала Лена?
РЕШЕНИЕ: Девочки сорвали 40 яблок. Нам необходимо найти количество яблок, которые съели вместе Лена и Света. Для этого нужно, от количества сорванных яблок вычесть сумму (15+9) оставшихся яблок у девочек.

Решение: 40 - (15+9) =40-24=16.
Девочки съели яблок поровну, поэтому мы решаем так: 16:2=8 (потому что их двое).
Каждая из девочек съела 8 яблок.
У Светы осталось 9 яблок, у Лены - 15. Теперь можем узнать количество сорванных яблок Леной.
Прибавляем всё, что осталось у Лены к числу 8. Решение: 15+8=23.
Лена сорвала 23 яблока.
Можно проверить: 23-8=15. (У Лены оставалось 15 яблок).
Теперь можно узнать количество сорванных яблок Светой. Решение: 40-23=17.
Света сорвала 17 яблок, а. Лена сорвала 23 яблок. Число 40 - это количество сорванных яблок девочками. Можно проверить: 23+17=40.
ОТВЕТ: Лена сорвала 23 яблок.

40. Бабушка купила на рынке курицу за 25 рублей.
Несет ее домой, навстречу 3 парня. «Бабушка, продай курицу за 30 рублей». «Берите». Пришла домой, решила вернуть 5 рублей. Посылает к парням внука с 5-ю рублями. Внук точно разделить 5 рублей не смог... Отдал по 1рублю, а остальное парни оставили ему на мороженое...
РЕШЕНИЕ:
Шаг1. У парней 30р, у бабки 25, у внука 0, у продавца курица.
Бабка покупает курицу
Шаг2. У парней 30р, у бабки курица, у внука 0, у продавца 25р.
Бабка продает курицу парням.
Шаг3. У парней курица, у бабки 30р, у внука 0, у продавца 25р.
Бабка отправляет внука.
Шаг4. У парней курица , у бабки 25р, у внука 5р, у продавца 25р.
Внук отдает парням по рублю.
Шаг5. У парней курица и 3 рубля, у бабки 25р, у внука 2 рубля, у продавца 25р.

41.Кузнецу принесли 5 обрывков цепи по 3 звена в каждом и поручили соединить их в одну цепь из пятнадцати звеньев. Кузнец выполнил заказ, расковав и заковав 4 звена. Как он сделал? Другой кузнец сказал, что заказ можно выполнить, раскатав и заковав только з звена. Как это можно сделать?

РЕШЕНИЕ:

оос оос оос оос ооо (4)

ооо с ооо с ооо с ооо (3)

42.При делении некоторого числа и на 13, и на 15 получились одинаковые частные. При делении на 13 получился остаток, равный 8, а при делении на 15 остатка не было. Найди это число. (60)

43.Сколько нулей получится в произведении всех натуральных чисел от 5 до 25? (12)

44. На какое число надо разделить 87912, чтобы получилось пятизначное число, записанное теми же цифрами, но в обратном порядке? (4)

Комбинаторные задачи

Решение таких задач дает возможность расширять знания учащихся о самой задаче, например, о количестве и характере результата (задача может иметь не только одно, но и несколько решений – ответов или не иметь решения), о процессе решения (чтобы решить задачу, не обязательно выполнять какие – либо действия). Учащиеся также знакомятся с новым методом решения задач. На комбинаторных задачах идет обучение методу перебора, решение задач с помощью таблиц, графов, схемы-дерева.

Кроме того, целенаправленное обучение решению комбинаторных задач способствует развитию такого качества мышления, как вариативность. Под ней понимается направленность мыслительной деятельности ученика на поиск различных решений задачи в случае, когда нет специальных указаний на это».

Сложность комбинаторных задач заключается в том, что при их решении должна быть выбрана такая система конструированного перебора, которая давала бы полную уверенность в том, что рассмотрены все возможные случаи (без повтора комбинаций). Перебор всегда осуществляется по какому-либо признаку объектов и напрямую связан с операцией классификацией объектов. Поэтому важным элементом готовности ребенка к овладению способами решения комбинаторных задач является его умение выделять различные признаки предметов, классифицировать множества одних и тех же объектов по различным основаниям. Комбинаторные задачи, составленные на жизненном материале, помогают школьникам лучше ориентироваться в окружающем мире, учат рассматривать все имеющиеся возможности и делать оптимальный выбор.

Комбинаторные задачи направлены на формирование умения использовать разные виды графовых схем, требуют сочетания эвристического и алгоритмического стиля мышления.

I этап. Подготовительный.

Цель: Совершенствовать мыслительные операции (анализ, синтез, сравнение) учащихся.

1.На каждой парте по три кубика: красный жёлтый и синий. Дети работают в парах. Необходимо составить из трех одинаковых по размеру кубиков красного, желтого и синего цвета несколько отличающихся друг от друга построек.

(Дети хаотично переставляют кубики, считают, сколько различных вариантов получилось. На первый стол выносят все шесть вариантов, необходимо поставить их так, чтобы рядом были постройки с одинаковыми нижними кубиками.)

2. Нарисуйте, как по-разному можно положить в ряд на столе тарелку, нож и вилку. Какой вариант будет более удобным для человека, который ест с помощью ножа и вилки?

II этап. Обучающий.

Цель: научить детей находить все возможные варианты в комбинаторных задачах, организуя перебор в определенной системе.

3.Смешарики решили, что у них должен быть свой флаг. Они выбрали три цвета: желтый, синий, красный. Раскрасьте флажки в эти цвета так, чтобы они отличались друг от друга. Сколько флажков получилось?

(В этом задании три полоски и три цвета. Число возможных перестановок цветов шесть. После того как дети выпол­нят задание, следует обсудить, как они действовали. Возможно, найдутся ученики, которые, раскрашивая полоски, действовали не хаотично, а соблю­дали определенный порядок раскрашивания.)

4.Нюше на день рождения подарили три мячика: желтый, зелёный и красный.

Нарисуйте, в каком порядке она может расположить их на полке. .

При обсуж­дении задания важно обратить внимание детей на рациональный способ действия: в первых двух случаях первые мячи одинаковые, а переставля­ются второй и третий; в третьем и четвертом случаях на первом месте появ­ляется тот мяч, который был вторым, а два других переставляются; в пятом и шестом случае на первом месте оказывается третий мяч, а два других опять меняются местами.

Друзья решили поиграть двумя мячиками. Какие из трех они могут выбрать. Нарисуйте все возможные варианты.

5.Для гербария Знайка выбрал три листа клена: зеленый, желтый, красный. Покажи, в каком порядке он может расположить их в альбоме.

(Обсуждается рациональный способ действия). Далее идет самостоятельная работа в тетрадях.

6.У Мальвины было 6 яблок. Из них 4 красных и 2 зеленых. Нарисуйте эти яблоки в своей тетради.

а) Буратино съел 2 яблока. Какого цвета могли быть эти яблоки? Раскрасьте заготовки.

(Детям необходимо следить за тем, чтобы пары отличались друг от друга. Четвертая пара яблок – «ловушка»).

б)Буратино съел 3 яблока. Какого цвета могли быть эти яблоки? Раскрасьте заготовки.

(Четвертая тройка яблок – «ловушка»).

в) Буратино съел 4 яблока. Какого цвета могли быть эти яблоки? Раскрасьте заготовки.

(Четвертый рисунок вновь – «ловушка»).

7. Гена принес Чебурашке три яблока разного цвета: зеленое, желтое и красное. Нарисуйте эти яблоки в своей тетради.

а) Покажите, как можно разложить эти яблоки по-разному друг за другом

(Важно вновь обратить внимание на рациональный способ действия. Фиксируем один цвет.)

8. У Чебурашки 5 разноцветных кубиков. Нарисуйте эти кубики.

а) Гена предложил построить башню из двух кубиков. Покажите на рисунке, какие варианты выбора двух кубиков из пяти возможны?

б) Чебурашка предложил выбрать три кубика из пяти. Сколько вариантов выбора получится в данном случае? Раскрасьте эти варианты.

9. У Пятачка было 4 шарика разного цвета.

Он решил подарить два шарика Ослику Иа. Нарисуйте все возможные варианты выбора. Сколько их получится? Как работать более рационально?

10.В алфавите пришельцев из космоса всего три буквы: Т, К, О.Составьте и запишите слова из трех букв, которые могут быть в речи инопланетян.

(Кот, кто, тко, ток, отк, окт).

- Какие слова употребляются в русской речи? (Кот, кто, ток).

11.Ребята, четверо инопланетян встречают нас.

Чтобы показать нам своё гостеприимство они исполняют свой национальный танец. Сколькими различными способами они могут стоять рядом друг с другом.

12.На этой планете все дома с круглыми окнами. Окон может быть в доме три, причем все они должны быть разного цвета. А вот любимые цвета здесь зеленый, желтый, синий и красный. Сколько разных наборов окон может быть на этой планете? Нарисуйте все их. Как работать более рационально?

(Фиксируем один цвет.)

III этап. Закрепляющий.

Цель: Научить детей производить перенос с одних объектов на другой на примере графов, знакомство с понятием «граф», его элементами.

1. На уроке физкультуры играли в теннис 4 мальчика: Дима, Ваня, Костя, Сергей. Какие были пары игроков, если все они сыграли друг с другом по одному разу?

Запишите условия задачи в виде схемы, где игроки обозначаются точками, а отношения «сыграли» - отрезком, соединяющим пару соответствующих точек

Дима Ваня,

Костя Сергей.

Выбираем одного игрока и выписываем пары, которые получились с ним, одновременно отмечая их на чертеже, затем другого игрока и выписываем те пары с ним, которые еще не отмечены и т.д. Схемы, подобные данной, носят название граф (от греческого пишу, черчу, рисую). Точки, которыми обозначили игроков, называются вершинами графа, а отрезки, их соединяющие, - ребрами графа.

2. Мама решила сварить компот. У неё было четыре фрукта: яблоки, вишни, груши и персики. Какие могли получиться напитки, если брать только по два фрукта? Необходимо самостоятельно составить схему и выписать пары.

3. Три реки Дон, Северский Донец и Сал протекают в городах Семикаракоры, Ростов, Каменск. Северский Донец протекает не в Семикаракорах, а Дон не в Каменске и не в Семикаракорах. Река Ростова имеет длину не 798 км. Та река, которая течет в Каменске длиной 1053км. . Определите местонахождение и длину каждой реки.

1 шаг: определяем местонахождение каждой реки.

	Ростов	Каменск	Семикаракоры
Дон	+	-	-
Северский Донец		+	-
Сал			+

2 шаг: определить длину каждой реки – составить таблицу.

	1870км	1053км	798км
Дон	+		-
Северский Донец		+
Сал			+

4.Инопланетяне сообщили жителям Земли, что в системе их звезды есть три планеты А, Б, В. Они живут на второй планете. Далее пере­дача ухудшилась из-за помех, но было принято еще два сообщения, которые, как установили ученые, оба неверные:

1) А — не третья от звезды планета;

2) Б — вторая планета.

На какой планете (А, Б, или В) живут инопланетяне?

	1	2	3
А			+
Б
В	+

А — не третья от звезды планета — это сообщение неверно. Значит, А — третья планета.

Б — вторая планета — тоже неверно. Значит, Б — первая пла­нета.

Остается принять, что В — вторая планета.

Ответ. Разумные существа живут на планете В.

5. У Вани, Толи и Миши есть собаки: пудель, овчарка и кокер - спаниель. У Миши не кокер - спаниель и не овчарка. У Вани не овчарка. У кого какая собака?

есть нет

Ваня пудель

Толя овчарка

Миша коккер-спаниель

Ваня пудель

Толя овчарка

Миша коккер-спаниель

Ваня пудель

Толя овчарка

Миша кокер – спаниель

6. В соревновании по бегу Антон, Володя и Сережа заняли три места. Какое место занял каждый из них, если Володя занял не второе и не третье место, а Сережа – не третье?

Антон 1

Володя 2

Сережа 3

нет

да

7.Старый волшебник разложил свои сокровища в четыре разноцветных сундука – красный, жёлтый, зелёный и синий. В один сундук он положил золотые монеты, в другой- изумруды, в третий – алмазы, а в четвёртый – книги заклинаний. Он помнит, что:

-жёлтый сундук правее, чем изумруды и алмазы;

- золотые монеты правее, чем жёлтый сундук;

-изумруды лежат не в красном сундуке.

1) В каком сундуке лежат книги заклинаний? (в жёлтом)

2) Что лежит в красном сундуке, если он стоит левее, чем жёлтый? (алмазы)

8.Принцесса разложила свои сокровища в четыре разноцветные коробки -фиолетовую, розовую, бордовую и оранжевую. В одну коробку она положила жемчужные ожерелья, в другую -золотые браслеты, в третью – письма принца. Она помнит, что:

-фиолетовая левее, чем драгоценные камни и жемчужные ожерелья;

- золотые браслеты левее, чем фиолетовая коробка;

- драгоценные камни лежат не в розовой коробке.

В какой коробке лежат письма принца? (в розовой)

В какой коробке лежат драгоценные камни, если самая левая коробка оранжевого цвета? (в бордовой)

9. Изюм, орехи, конфеты и мармелад лежат в четырёх непрозрачных банках с надписями «изюм или орехи», «конфеты или изюм», «мармелад или конфеты», «орехи или мармелад». Пете известно, что содержимое каждой из банок не соответствует сделанной на ней надписи. Открыв банку с надписью «орехи или мармелад», Петя увидел, что в ней лежит изюм.

В банке с какой надписью лежат конфеты? (в банке «изюм или орехи»)

Что лежит в банке с надписью «конфеты или изюм»? (мармелад)

Задачи логические и комбинаторные.

Задача №1.

Если Лена купит 3альбома, то у неё останется 40 рублей. А если бы она захотела купить 5 альбомов, ей не хватило бы 200 рублей. Сколько денег у Лены?

Решение.

1. 5-3=2(аль.) – разница.

2. 40+200=240(руб)- стоят 2 альбома.

3. 240:2=120(руб)- стоит 1 альбом.

4. 120*3+40=400(руб)-было у Лены

Ответ: 400 рублей.

Задача №2.

Витя, Коля, Саша и Дима играли с мячами синим, зелёным, жёлтым и красным. Каким из мячей играл каждый из них, если мяч Вити не синий, у Коли не синий и не красный, а у Саши желтый мяч?

Решение.

	Витя	Коля	Саша	Дима
Синий	-	-
Зеленый
Желтый			+
Красный		-

Синий может быть только у Димы.

	Витя	Коля	Саша	Дима
Синий	-	-		+
Зеленый
Желтый			+
Красный		-

Ответ: Красный только у Вити, Коле остался зеленый.

Задача №3.

Если к Колиным деньгам добавить ещё половину его денег и ещё 30 рублей, он сможет купить диск с игрой и машинку. Сколько денег у Коли, если игра стоит 200 рублей или 2 машинки.

Решение.

1. 200: 2= 100(руб)- стоит машинка.

2. 200+100=300(руб) - стоит машинка и диск.

3. 300-30=270(руб)- деньги, которые были у Коли и половина его денег.

4. 2+1=3(мерки)- составляют деньги Коли и половина его денег.

5. 270:3=90(руб)- в одной мерке

6. 90*2=180(руб)- было у Коли

Ответ: 180 рублей.

Задача №4.

В сказочной стране у волшебных человечков по 3 руки. Двадцать человечков построились в шеренгу, и каждый взял соседа за руку. Сколько рук осталось свободными?

Решение. У каждого человечка 2 руки заняты, а одна свободна. У крайних человечков свободны ещё по 1 руке.

Ответ: 22 руки

Задача №5.

 10 жуков построились в шеренгу, каждый взял за лапку каждого из своих соседей. Сколько всего лапок оказались свободными?

Решение.

У каждого жука 2 лапки заняты, а остальные 4 свободны, ещё 2 крайние лапы

Ответ: 42 лапы.

Задача №6.

Лена начертила 20 фигур: треугольников и квадратов. Всего она провела 72 отрезка.   Сколько квадратов она начертила?

Решение. Если бы все 20 фигур были треугольниками, то отрезков бы было 60. Остается 12 отрезков, добавив которые к треугольникам, получим 12 квадратов

Ответ: 12 квадратов.

Задача №7.

Два друга живут в одном доме. До школы ведут две дороги: синяя и красная. Коля любит ходить по синей дороге, а Саша по красной. Кто быстрее дойдет до школы, если идти будут с одинаковой скоростью?

Задача №8.

Буратино, Мальвина и Пьеро катались на велосипедах. У них были трехколёсные и двухколёсные велосипеды, всего было 8 колёс. Сколько было трехколёсных велосипедов? (2 – трехколесных и 1 – двухколесный)

Задача №9.

Из 25 человек класса 17 изучают английский язык, а 15 – французский, причем каждый ученик класса изучает один из этих языков. Сколько детей изучает оба эти языка?

Решение.

1. 25 – 15 = 10(ч)- не изучают французский язык
2. 25 – 17 = 8 (ч)- не изучают английский язык
3. 10 + 8 = 18(ч)-изучают только один язык (французский или английский)
4. 25 – 18 = 7 (ч)- изучают оба языка.

Ответ: 7человек

Задача №10.

Стас по лесу шел

И колечко нашел.

А с Леной пойдет,

Тогда сколько найдет?

(На этот вопрос ответить нельзя.)

Задача №11.

В песочнице играли 6 мальчиков и 3 девочки. Четырёх детей позвали мамы. Ушёл хотя бы один мальчик? (Да, если все дети послушные.)

Задача №12.

В двух корзинах лежало одинаковое количество яблок. Из первой корзины во вторую переложили 10 яблок. На сколько больше стало яблок во второй корзине, чем в первой?

Решение. Так как из первой корзины во вторую переложили 10 яблок, то в ней увеличилось на 10 яблок , а в первой уменьшилось на 10. Всего разница составляет 20 яблок.

Ответ: на 20 больше.

Задача №13.

Буратино, Мальвина и Пьеро катались на велосипедах. У них были трехколёсные и двухколёсные велосипеды, всего было 8 колёс. Сколько было трехколёсных велосипедов? (2 – трехколесных и 1 – двухколесный)

Задача №14.

Во дворе гуляли куры и собаки. Мальчик посчитал их лапы, получилось 10 лап. Сколько могло быть кур и собак?

(2 собаки и 1 курица, или 1 собака и 3 курицы).

Задача №15.

5 ребят катались на велосипедах. Дима посчитал рули и колеса. Рулей оказалось 4, а колес – 10. Как это может быть?

Ответ: велосипедов 4, 2 из них двухколесные, а 2 трехколесные.

Задача №16.

В трёхэтажном доме жили три котёнка: белый, чёрный и рыжий. Котята с первого и второго этажей не были чёрными. Белый котёнок жил не на первом этаже. Какой котенок, на каком этаже жил?

Решение. Так как котята с первого и второго этажей не были чёрными, значит чёрный котёнок жил на третьем этаже. Белый котёнок жил не на первом этаже, значит он жил на втором. На первом этаже жил рыжий котёнок.

Задача №17.

 В коробке лежит 4 шарика: черных, белых и красных. Красных шариков столько же, сколько белых и черных вместе. Сколько черных шариков в коробке?

Решение. Красные шарики составляют половину всех шариков, то есть их 2. Черных и белых шариков вместе 2. Значит, их по одному каждого цвета.

Ответ: черных 1, белых 1, красных 2.

Задача №18.

Катя, Света и Ира написали контрольную работу по математике. Они спросили у учителя, какая у них отметка. Учитель ответил: «Попробуйте догадаться. В классе двоек нет и у вас у всех отметки разные, причем, у Кати не три, а у Иры не три и не пять».

Решение.

Так как у Иры не три и не пять, значит у неё четыре. У Кати не три и не четыре, значит у неё пять. Свете остаётся тройка.

Задача №19.

Мама, папа и Таня пошли за грибами. Они взяли корзину, ведерко и лукошко. Мама была не с корзиной и не с лукошком, папа не с лукошком. Что было в руках у Тани?

Решение. Мама была не с корзиной и не с лукошком, значит с ведерком. Папа не с лукошком, значит с корзиной. Тане достаётся лукошко.

Ответ: в руках у Тани было лукошко.

Задача №20.

Света, Ира и Лена купили шарики разного цвета: белый, красный, голубой. Какой шарик купила каждая из них, если известно, что у Светы - не голубой и не красный, у Иры - не голубой?

Решение. Светы не голубой и не красный шарик, значит он у неё белый. У Иры не голубой, значит красный. У Лены голубой шарик.

Задача №21.

Кирилл, Дима и Стас участвовали в теннисном турнире. Все оказались на пьедестале. Кирилл не занял второго места. Дима не занял ни первого, ни второго места. Какое место занял каждый из мальчиков?

Решение. Дима не занял ни первого, ни второго места, значит, он занял третье место. Кирилл не занял второго места, значит, он занял первое место. Стас занял вторе место.

Задача №22.

В красный, синий и зелёный стакан налили молоко, простоквашу и кефир. В красном не кефир. В синем не кефир, и не простокваша. Что куда налили?

Решение. В синем не кефир, и не простокваша, значит, там молоко. В красном не кефир, значит, там простокваша. В зеленом стакане кефир.

Задача №23

Для украшения зала повесили 17 шариков: синих, жёлтых и красных. Красных шариков в 8 раз больше, чем жёлтых. Сколько повесили синих шариков?

Решение. Жёлтых шариков не может быть больше одного, так как если бы их было хотя бы 2, то красных шариков было бы не меньше 16. 16+2=18, а шариков всего 17. Значит, жёлтых шарик всего один, а красных в 8раз больше, то есть 8. Синих шариков 17 – (1 + 8) = 8.

Ответ: синих -8 штук, жёлтых-1 штука, красных -8 штук.

Решение комбинаторных задач перебором, графами и таблицами.

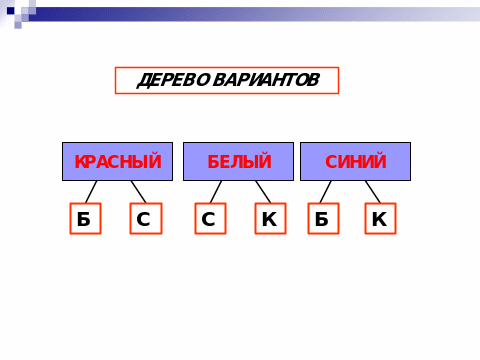
1. Государственные флаги некоторых стран состоят из трех горизонтальных полос разного цвета. Сколько различных вариантов флагов с белой, синей и красной полосами можно составить?

Решение этой задачи можно записать двумя способами:

1. Таблица вариантов

КБС	КСБ
БСК	БКС
СБК	СКБ

1. Дерево вариантов

2.«Коля, Боря, Вова, Юра заняли первые четыре места в соревнованиях. На вопрос, какие места они заняли, трое ответили: Коля – ни 1-е, ни 4-е; Боря – 2-е; Вова – не 4-е. Какие места заняли мальчики?».

Составляется таблица исходных данных:

Место	Коля	Боря	Вова	Юра
1	–	–	+	–
2	–	+	–	–
3	+	–	–	–
4	–	–	–	+

3. В танцевальном кружке занимаются 5 девочек: Женя, Маша, Катя, Юля, Даша и 5 мальчиков: Олег, Вова, Стас, Андрей и Иван. Сколько различных танцевальных пар можно составить? (25)

Женя Женя Женя Женя Женя

Олег Вова Стас Андрей Иван

Маша Маша Маша Маша Маша

Олег Вова Стас Андрей Иван

Катя Катя Катя Катя Катя

Олег Вова Стас Андрей Иван

Юля Юля Юля Юля Юля

Олег Вова Стас Андрей Иван

Даша Даша Даша Даша Даша

Олег Вова Стас Андрей Иван

4. «Беседуют трое друзей: Белокуров, Рыжов и Чернов. Брюнет сказал Белокурову: «Любопытно, что ни у кого из нас цвет волос не соответствует фамилии, да и ты не брюнет». Какой цвет волос у каждого из друзей?»

Составляется таблица исходных данных:

	Блондин	Брюнет	Рыжий
Белокуров	-	-	+
Рыжов	-	+	-
Чернов	+	-	-

5. Миша, Сережа, Дима, Валера и Костя рисовали машины:

• кто-то рисовал пожарную машину красным карандашом;

• кто-то гоночную машину синим фломастером;

• кто-то - грузовик коричневой ручкой;

• кто-то - легковую машину синим карандашом;

• кто-то - легковую машину коричневым фломастером.

Миша и Сережа рисовали карандашом. Сережа и Дима рисовали одинаковым цветом. Валера рисовал не фломастером. Кто что рисовал?

Составляется таблица исходных данных:

	пожарную машину красным карандашом	гоночную машину синим фломастером	грузовик коричневой ручкой	легковую машину синим карандашом	легковую машину коричневым фломастером
Миша	+			+-
Серёжа	+ -			+
Дима		+
Валера			+		-
Костя					+

6. Путешественник хочет выехать на своей машине из города А, посетить города В, С и D, после чего вернуться в город А. Какими путями можно это сделать? На рисунке схема путей, связывающих города. Какой из вариантов самый оптимальный?

7. Саша ходит в школу в брюках или джинсах, к ним надевает рубашки серого, голубого, зеленого цвета или в клетку, а в качестве сменной обуви берет туфли или кроссовки.
а) Сколько дней Саша сможет выглядеть по-новому?
б) Сколько дней при этом он будет ходить в кроссовках?
в) Сколько дней он будет ходить в рубашке в клетку и джинсах?

Решение. Построим дерево возможных вариантов, обозначив Б - брюки, Д - джинсы, С - серая рубашка, Г - голубая рубашка, З - зеленая рубашка, Р - рубашка в клетку, Т - туфли, К - кроссовки.

 

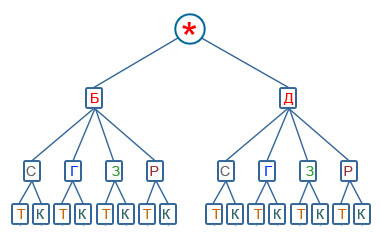
Ответ: а) 16 дней Саша может выглядеть по-новому;

б) 8 дней он будет ходить в кроссовках;

в) 2 дня он будет ходить в рубашке в клетку и джинсах.

8. Школьные туристы решили совершить путешествие к горному озеру. Первый этап пути можно преодолеть на поезде или автобусе. Второй этап - на байдарках, велосипедах или пешком. И третий этап пути - пешком или с помощью канатной дороги. Какие возможные варианты путешествия есть у школьных туристов?

Решение. Построим дерево возможных вариантов, обозначив путешествие на поезде П, на автобусе - А, на байдарках - Б, велосипедах - В, пешком - Х, на канатной дороге - К.

 

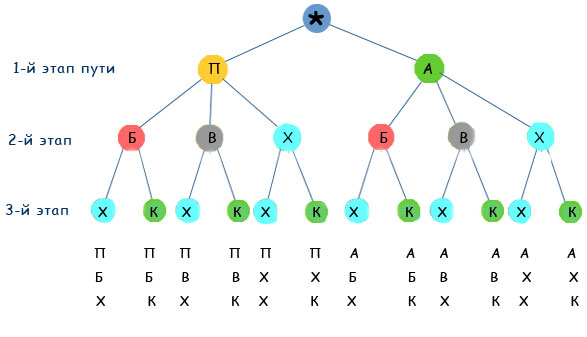
Ответ: На рисунке перечислены все 12 возможных вариантов путешествия школьных туристов.

9. Маша, Оля, Вера, Ира, Андрей, Миша и Игорь готовились стать ведущими на Новогоднем празднике. Назовите возможные варианты, если ведущими могут быть только одна девочка и один мальчик.

Решение. Составим таблицу: слева первый столбец - имена девочек, вверху первая строка - имена мальчиков.

	Андрей	Миша	Игорь
Маша	Маша-Андрей	Маша-Миша	Маша-Игорь
Оля	Оля-Андрей	Оля-Миша	Оля-Игорь
Вера	Вера-Андрей	Вера-Миша	Вера-Игорь
Ира	Ира-Андрей	Ира-Миша	Ира-Игорь

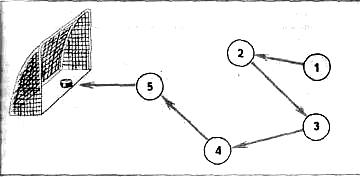
10.  На поле 5 игроков. Начал комбинацию игрок № 1, продолжили игроки с другими номерами, а забил гол игрок № 5. Каждый хоккеист ударил по шайбе только один раз. На рисунке с помощью стрелок изображен один из возможных вариантов передачи шайбы между игроками в данной комбинации. Изобразите в тетради все другие возможные варианты передачи шайбы.

44