Первый тур (12 минут; каждая задача – 6 баллов)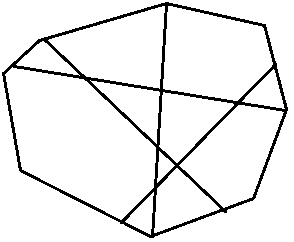
1.1.Отцу 41 год, старшему сыну 13 лет, дочери 10, а младшему сыну 6 лет. Через сколько лет возраст отца будет равен сумме возрастов трех его детей?
Решение:
Пусть через х лет возраст отца будет равен сумме возрастов трех его детей. Тогда,
Отцу – 41+х;
Сыну – 13+х;
Дочери – 10+х;
Младшему сыну – 6+х. По условию возраст отца равен сумме возрастов детей.
41+х=13+х+10+х+6+х;
Х=6.
Ответ: 6 лет.
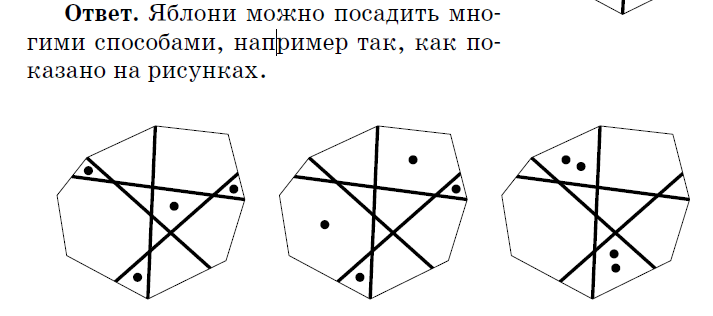
1.2.Через двор проходят четыре пересекающиеся тропинки (см. план). Посадите четыре яблони так, чтобы по обе стороны от каждой тропинки было поровну яблонь.
1.3.В этих математических примерах вместо знаков «+» и «-» нарисованы кружки. Расставьте знаки так, чтобы получились верные равенства.
а) 2 О 6 О 3 О 4 О 5 О 8 = 12
б) 9 О 8 О 1 О 3 О 5 О 2 = 12
в) 8 О 6 О 1 О 7 О 9 О 2 = 12
г) 7 О 9 О 8 О 4 О 3 О 5 = 12
д) 3 О 2 О 1 О 4 О 5 О 3 = 12
Решение:
а) 2 + 6 - 3 + 4 - 5 + 8 = 12
б) 9 + 8 + 1 - 3 - 5 + 2 = 12
в) 8 О 6 О 1 О 7 О 9 О 2 = 12, в данной сумме три нечетных числа, значит сумма будет нечетной, а 12 четное.
г) 7 О 9 О 8 О 4 О 3 О 5 = 12, в данной сумме три нечетных числа, значит сумма будет нечетной, а 12 четное.
д) 3 - 2 - 1 + 4 + 5 + 3 = 12
Второй тур (15 минут; каждая задача – 7 баллов)
2.1. У Пети средний бал по математике был равен 3,5. Он получил за домашнюю работу пятерку, и средний бал стал равен 4. Сколько всего оценок у Пети по математике?
Решение:
Пусть у Пети n оценок. Так как средний балл равен 3,5, то сумма всех баллов равна 3,5n.
После того, как он получил «5», сумма баллов равна 3,5n+5. С другой стороны, средний балл стал равен 4, и сумма всех баллов равна 4(n+1). 3,5n+5=4(n+1).n=2. И еще одна «5».
Ответ: 3.
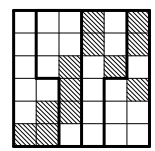
2.2. Разрежьте квадрат 6×6 из клетчатой бумаги, изображенный на рис. 12, на четыре одинаковые части так, чтобы каждая из них содержала три закрашенные клетки. 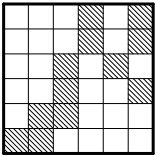
2.3.Вдоль забора растут 8 кустов малины. Число ягод на соседних кустах отличается на 1. Может ли на всех кустах вместе быть 2015 ягод?
Решение:
Число ягод на соседних кустах отличается на 1, то число ягод на одном из кустов четно, а на другом нечетно, поэтому на двух соседних кустах вместе нечетное количество ягод, т. к сумма четного и нечетного числа есть число нечетное. Тогда количество ягод на восьми кустах равно сумме четырех нечетных чисел, т. е четному числу, число 225 -нечетное. Значит, на всех кустах вместе не может расти 225 ягод.
Ответ: нет
Третий тур (18 минут; каждая задача – 8 баллов)
3.1. Двое одновременно отправились из A в B. Первый поехал на велосипеде, второй – на автомобиле со скоростью, в пять раз большей скорости первого. На полпути с автомобилем произошла авария, и оставшуюся часть пути автомобилист прошел пешком со скоростью, в два раза меньшей скорости велосипедиста. Кто из них раньше прибыл в B?
Решение:
Пусть скорость велосипедиста 2х. Тогда скорость автомобиля – 10х, а пешехода х. И пусть все расстояние 2s. Тогда время движения велосипедиста 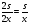 , а время движения автомобилиста
, а время движения автомобилиста 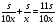 .
. 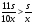 , значит время велосипедиста меньше, следовательно он раньше прибыл в пункт В.
, значит время велосипедиста меньше, следовательно он раньше прибыл в пункт В.
3.2.Электронные часы показывают время от 00.00.00 до 23.59.59. Сколько времени в течении суток на табло часов в каком-то месте горит число 2015? (цифры должны идти подряд).
Решение:
Рассмотрим все варианты образования числа 2015.
20.15.ХХ – горит 60 сек.
Х2.01.5Х – горит 3*10=30 сек.
ХХ.20.15. – горит 24 сек. Итого: 60+30+24=114 сек.
3.3.На доске написаны числа 1, 2, 3, …, 50. Разрешается стереть с доски любые два числа и вместо них записать модуль их разности. Может ли на доске остаться число ноль?
Решение:
Данная сумма содержит
Сумма: 1+2+3+…+50 содержит 25 нечетных чисел. Сумма нечетного количества нечетных чисел – нечетна.
Заметим, что проводя данную операцию четность суммы не изменяется.
Н-(ч+ч)+ч=н,
Н-(н+н)+ч=н,
Н-(н+ч)+н=н.
А ноль, число четное. Значит, ноль получить нельзя.
Ответ: нельзя.











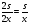 , а время движения автомобилиста
, а время движения автомобилиста 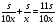 .
. 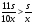 , значит время велосипедиста меньше, следовательно он раньше прибыл в пункт В.
, значит время велосипедиста меньше, следовательно он раньше прибыл в пункт В.









