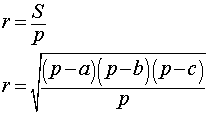Прямая Ньютона — это прямая, которая соединяет середины двух диагоналей выпуклого четырехугольника, имеющего не более двух параллельны сторон.
Эта прямая имеет несколько интересных геометрических свойств. В частности, отрезки, соединяющие середины противоположных сторон выпуклого четырёхугольника, пересекаются в точке, лежащей на прямой Ньютона. Если четырёхугольник является описанным, его инцентр также лежит на этой прямой.
Средние линии четырехугольника
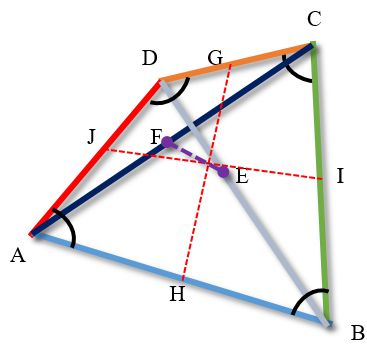 У каждого четырехугольника есть три средние линии.
Средними линиями несамопересекающегося четырехугольника называются отрезки, соединяющие середины его противолежащих сторон (первая и вторая) и отрезок, соединяющий середины его диагоналей.
На рисунке средние линии четырехугольника отмечены пунктирными линиями.
У каждого четырехугольника есть три средние линии.
Средними линиями несамопересекающегося четырехугольника называются отрезки, соединяющие середины его противолежащих сторон (первая и вторая) и отрезок, соединяющий середины его диагоналей.
На рисунке средние линии четырехугольника отмечены пунктирными линиями.
Центроид четырехугольника
Центроидом четырехугольника называется точка пересечения всех его средних линий.
Обобщенная теорема Ньютона
Средние линии несамопересекающегося четырехугольника, образуемые серединами противолежащих сторон (первая и вторая средняя линия) и отрезком, соединяющим середины диагоналей (третья средняя линия) пересекаются в одной точке и делятся ею пополам.
Прямая, проходящая через середины диагоналей четырехугольника и его центроид также называется прямой Ньютона.
Задача.
Докажите что биссектрисы острых углов прямоугольного треугольника при пересечении образуют угол 45.
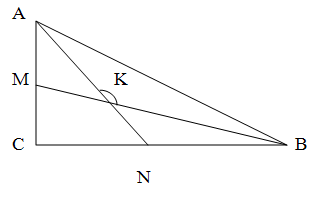 Решение.
Поскольку сумма углов треугольника равна 180 градусам, угол С в данном случае прямой, то сумма двух оставшихся углов составляет 180 - 90 = 90 градусов.
Поскольку BM и AN - биссектрисы, а сумма их градусных мер составляет 90 градусов, то сумма половин этих углов ( KAB и KBA) составляет 90 / 2 = 45 градусов. Таким образом, величина угла AKB в треугольнике AKB составляет 180 - 45 = 135 градусов.
Соответственно, величина угла MKA равна 180 -135 = 45 градусов. То есть биссектрисы прямоугольного треугольника образуют угол 45 градусов.
Таким образом, при пересечении биссектрисы прямоугольного треугольника образуют углы 45 и 135 градусов.
Решение.
Поскольку сумма углов треугольника равна 180 градусам, угол С в данном случае прямой, то сумма двух оставшихся углов составляет 180 - 90 = 90 градусов.
Поскольку BM и AN - биссектрисы, а сумма их градусных мер составляет 90 градусов, то сумма половин этих углов ( KAB и KBA) составляет 90 / 2 = 45 градусов. Таким образом, величина угла AKB в треугольнике AKB составляет 180 - 45 = 135 градусов.
Соответственно, величина угла MKA равна 180 -135 = 45 градусов. То есть биссектрисы прямоугольного треугольника образуют угол 45 градусов.
Таким образом, при пересечении биссектрисы прямоугольного треугольника образуют углы 45 и 135 градусов.
Свойства вписанной окружности
- В каждый треугольник можно вписать окружность, при этом только одну
- Центр вписанной окружности называется инцентром, он равноудалён от всех сторон
- Центр вписанной окружности является точкой пересечения биссектрис треугольника
Радиус вписанной окружности
Радиус вписанной в произвольный треугольник окружности равен отношению его площади к полупериметру.
Формулы радиуса вписанной окружности:
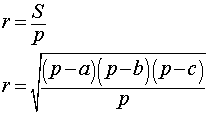
Центр вписанной в треугольник окружности - это точка пересечения биссектрис его улов. При этом стоит заметить, что для равнобедренного треугольника - биссектриса угла напротив основания - является одновременно и высотой.







 У каждого четырехугольника есть три средние линии.
Средними линиями несамопересекающегося четырехугольника называются отрезки, соединяющие середины его противолежащих сторон (первая и вторая) и отрезок, соединяющий середины его диагоналей.
На рисунке средние линии четырехугольника отмечены пунктирными линиями.
У каждого четырехугольника есть три средние линии.
Средними линиями несамопересекающегося четырехугольника называются отрезки, соединяющие середины его противолежащих сторон (первая и вторая) и отрезок, соединяющий середины его диагоналей.
На рисунке средние линии четырехугольника отмечены пунктирными линиями. Решение.
Поскольку сумма углов треугольника равна 180 градусам, угол С в данном случае прямой, то сумма двух оставшихся углов составляет 180 - 90 = 90 градусов.
Поскольку BM и AN - биссектрисы, а сумма их градусных мер составляет 90 градусов, то сумма половин этих углов ( KAB и KBA) составляет 90 / 2 = 45 градусов. Таким образом, величина угла AKB в треугольнике AKB составляет 180 - 45 = 135 градусов.
Соответственно, величина угла MKA равна 180 -135 = 45 градусов. То есть биссектрисы прямоугольного треугольника образуют угол 45 градусов.
Таким образом, при пересечении биссектрисы прямоугольного треугольника образуют углы 45 и 135 градусов.
Решение.
Поскольку сумма углов треугольника равна 180 градусам, угол С в данном случае прямой, то сумма двух оставшихся углов составляет 180 - 90 = 90 градусов.
Поскольку BM и AN - биссектрисы, а сумма их градусных мер составляет 90 градусов, то сумма половин этих углов ( KAB и KBA) составляет 90 / 2 = 45 градусов. Таким образом, величина угла AKB в треугольнике AKB составляет 180 - 45 = 135 градусов.
Соответственно, величина угла MKA равна 180 -135 = 45 градусов. То есть биссектрисы прямоугольного треугольника образуют угол 45 градусов.
Таким образом, при пересечении биссектрисы прямоугольного треугольника образуют углы 45 и 135 градусов.