Муниципальное общеобразовательное учреждение
Деяновская основная школа
Пильнинского муниципального района
Нижегородской области
Исследовательская работа
«Математика в медицине»
Выполнил:
ученик 7 класса
Гущин Алексей
Руководитель:
Гущина М.Н.
Деяново 2018 год
Содержание
Введение……………………………………………………………………….3-4
Значение и области применения математики в медицине…………...5-10
Исследования , проводимые группой учащихся 7 класса в Деяновском фельдшерско- акушерском пункте.......................................................11-13
Расчёт пульса………………………………………………………11-12
. Расчёт максимально допустимого и субмаксимального пульса .....................................................................................................11-12
. Расчёт предполагаемого роста………………………………….13
Наблюдение за весом……………………………………………….13
3. Заключение……………………………………………………………….14
4.Список использованной литературы…………………………………...15
Введение
Вряд ли существует какая-то другая наука, помимо математики, которая бы имела такое же значение в жизни каждого отдельного человека и всего общества в целом. Мы встречаемся с математикой каждый день и повсюду — когда просыпаемся в доме, который должен быть построен согласно точным математическим расчётам, переходим дорогу на зелёный свет, который должен гореть определённое количество секунд. Ни секундой больше, но и не секундой меньше. От этого зависит жизнь людей. Приходя на место учёбы или работы, мы также сталкиваемся с математикой — урок длится 45 минут (как точно рассчитано для того, чтобы школьник мог учиться и не уставать!) и определённое количество времени на перемену. На работе — тем более.
В этой исследовательской работе будет подробно рассмотрена роль математики в медицине. Ведь вряд ли можно назвать область более важную, чем медицину. Основная причина — что без спасения физического здоровья, без гарантии самого физического выживания человека нельзя говорить о каком бы то ни было развитии человека.
Актуальность проекта: здоровье человека относится к глобальным проблемам, решение которых зависит от усилий отдельных профессиональных групп, к которым относятся работники медицины. Без знания азов математики нельзя быть докой в компьютерной технике, использовать возможности компьютерной томографии. Ведь современная медицина не может обходиться без сложнейшей техники. Со временем, все глубже и глубже изучая математику и наблюдая за процессом изменений и развития в области медицины, я нахожу между ними тесную взаимосвязь.
Цель исследования: выявление и установление взаимосвязи математики и медицины.
Объект исследования – учащиеся 7 класса.
Цель определила постановку следующих задач:
Формировать умения и навыки самостоятельного поиска информации и работы с ней;
Проанализировать функции математики в медицине;
Провести исследование среди учащихся, сделать сравнительный анализ результатов.
В своей работе я выдвинул следующую гипотезу: приступая к исследованию, я предположил, что если применение математики в медицине сделать наиболее частым, то можно увеличить продолжительность жизни людей.
Исследование проходило в три этапа:
Изучение теоретического материала о роли математики в медицине; Экспериментальная часть и анализ полученных результатов;
Разработка вывода, рекомендаций по применению математики в медицине.
1. Значение математики в медицине
 Математика широко используется во многих сферах человеческой и общественной жизни. При этом, безусловно, роль математики в точных науках общепризнанна, но ценность и целесообразность использования различных математических методов в «менее строгих» науках, среди которых особое место занимает медицина, часто ставится под сомнение. Такое мнение обусловлено изменчивостью различных факторов и их тесной взаимосвязью, которая характерна для медицинских исследований. В результате многие полагают, что применение математических методов в медицине вообще невозможно. Но на самом деле на наш взгляд это не так. Ведь действительно, чтобы проникнуть и понять исследуемые процессы, а в результате и управлять ими, принципиально важно подобрать математический аппарат, который предоставит возможность выполнять анализ на самом высоком уровне.
Математика широко используется во многих сферах человеческой и общественной жизни. При этом, безусловно, роль математики в точных науках общепризнанна, но ценность и целесообразность использования различных математических методов в «менее строгих» науках, среди которых особое место занимает медицина, часто ставится под сомнение. Такое мнение обусловлено изменчивостью различных факторов и их тесной взаимосвязью, которая характерна для медицинских исследований. В результате многие полагают, что применение математических методов в медицине вообще невозможно. Но на самом деле на наш взгляд это не так. Ведь действительно, чтобы проникнуть и понять исследуемые процессы, а в результате и управлять ими, принципиально важно подобрать математический аппарат, который предоставит возможность выполнять анализ на самом высоком уровне.
На сегодняшний день математические методы широко используют для описания различных медицинских процессов (в первую очередь это необходимо для установления болезненного и нормального функционирования организма, а также его различных систем). В результате благодаря полученным данным можно выбирать наиболее оптимальные направления диагностики и лечения пациента. Плюс ко всему следует добавить, что сейчас диагностика заболеваний на математической основе выступает для врача таким же важным инструментом, как расчеты для инженера. Она помогает установить действительно точный диагноз. Важность математических методов в современной медицине трудно переоценить, поскольку своевременно поставленный диагноз часто существенно облегчает выбор метода лечения и повышает вероятность выздоровления больного.
Но существуют и более удивительные случаи влияния математики на процесс выздоровления пациента. Так, например, любовь юной англичанки Вики Алекс к математике воистину спасла этой девушке жизнь. Летом 14-летняя школьница начала испытывать трудности с дыханием. Родные долго не могли понять, в чем дело, пока врачи не поставили страшный диагноз – рак крови. Длительное время Вики лечили от рака крови. Терапия протекала успешно. Но спустя некоторое время у девочки появились симптомы простуды. Потом на спине появилась какая-то шишка. Доктор решил, что это фурункул, и прописал антибиотики.
К сожалению, организм девочки, ослабленный тяжелым заболеванием, уже не справлялся с инфекцией. И тогда врачи решили поместить ее в своеобразную кому для использования лекарств. Шансы на то, что в этом состоянии лекарства подействуют, имелись, но не было никаких гарантий того, что Вики вновь придет в себя.
Через несколько дней врачи попытались вернуть девочку в сознание, но подросток не выходил из комы. И тогда лечащий врач Вики предложил ее родителям пообщаться с дочерью. Возможно, Вики могла бы отреагировать на голоса родных для себя людей. Целый час папа и мама обсуждали с дочерью ее друзей, любимые телепрограммы, певцов и моду. Никаких признаков восстановления сознания, к сожалению, не было.
И тогда отец Вики, решил прибегнуть в математике. "Она у меня всегда любила считать, - рассказывает Ник. - И я решил рискнуть. Мне не хотелось ее перегружать, я начал с самых простых задачек, вроде того, сколько будет один плюс один. И вдруг дочь ответила – шевельнулись губы. Я только не мог понять, что она говорит, поэтому спросил: "Ты хочешь сказать "два"?" Она едва заметно кивнула".
Постепенно Ник начал усложнять задания, а к его дочери медленно возвращалось сознание. Через несколько часов Вики Алекс полностью пришла в себя. Вот таким даже немного косвенным методом, но математика спасает жизнь!
Фармакология - это один из самых сложных предметов медицины. На сегодняшний день известно уже более 10000 различных лекарственных препаратов. При этом можно с полной уверенностью утверждать, что только с помощью высокоточных математических методов можно рассчитать взаимодействие данных препаратов в организме конкретного больного. Именно благодаря этим методам врачи получают возможность подобрать наиболее оптимальные дозы нужного препарата и в результате обеспечить максимально эффективное лечение и быстрое выздоровление пациента.
Особое значение в фармакологии получило математическое моделирование, которое помогает установить лечебную и смертельную дозы используемых лекарств. Чаще всего размеры устанавливаются экспериментальным методом, но далеко не во всех случаях полученные данные являются достоверными. В таком случае используется метод математического моделирования на базе полученной экспериментальным путем информации. В результате врачи получают возможность определять пределы дозировки лекарственных веществ и устанавливать своим пациентам эффективные программы лечения и последующего восстановления.
Так, например, именно благодаря математическим расчетам врач может установить дозу для своего пациента, которая будет не смертельной, а лечебной. Пренебрегать этим нельзя, поскольку неправильная дозировка может привести к летальным исходам.
Безусловно, существуют и обратные примеры. Так правильная дозировка позволяет значительно ускорить восстановление спортсменов после полученных травм и проведенных операций. К примеру, бывший игрок лондонского Арсенала и сборной Хорватии Эдуардо после перелома ноги восстановился всего лишь за 8 месяцев, хотя стандартный срок выздоровления после такого повреждения не менее года.
Области применения математики в медицине
1). Математика широко применяется в кардиологии. Современные приборы позволяют врачам «видеть» человека изнутри, правильно устанавливать диагноз и назначать эффективное лечение. Созданием таких приборов занимаются инженеры, использующие аппарат физико-математических исследований. Ритмы сердца и движение математического маятника, рост бактерий и геометрическая прогрессия, формула ДНК - все это примеры применения математических расчетов в медицине.
Год от года расширяется сфера использования вычислительных машин. С их помощью, а также при содействии телевидения стала возможной передача на расстояние электрокардиограмм тяжелобольных в центр и консультация специалистов. Разрабатываются специальные программы по диагностике заболеваний на расстоянии. Цифровые осциллографы ,аппарат для снятия ЭКГ. В медицинской практике используются математические модели для компьютерного анализа кардиограмм и распознавания болезней сердца.
2). Математика играет одну из главных ролей при создании и применении лекарств. Лечебный эффект лекарства зависит не только от вида составляющих, но и от пропорций, в которых они входят в него. Фармацевт должен уметь решать задачи на пропорцию и концентрацию растворов. На упаковке лекарства мы можем прочитать состав и количественные показатели ингредиентов, активных веществ, указания о норме и времени приема лекарства – и это тоже математика.
3). Математические основы компьютерной томографии были заложены задолго до появления первых рентгеновских компьютерных томографов. Еще в 1917 году математик И. Радон предложил метод решения обратной задачи интегральной геометрии, состоящий в восстановлении (реконструкции) многомерных функций по их интегральным характеристикам.
4). Математика широко применяется в микрохирурги глаза. Например, лазерная коррекция зрения - там очень точные расчеты.
Все действия лазера управляются компьютером, в который закладывается программа, с данными рассчитанными индивидуально для каждого пациента с максимальной точностью определяющая объем лазерной коррекции. " И даже для того, чтобы правильно подобрать очки, нужна математика.
5). Математика тесно связана с педиатрией. Ведь с математики начинается все. Ребенок только появился, а первые цифры в его жизни уже звучат: дата рождения, рост, вес. Вот многие, я уверен, не знали, что кормление ребёнка требует подсчёта формул. Или то, что есть формулы подсчёта давления у новорождённого ребёнка. Сколько должен ребенок весить при определенном росте, какое должно быть давление, какой рацион питания применять?
Вышеперечисленные области применения математики далеко не все. На многих знакомых нам медицинских приборах и аппаратах мы увидим шкалы – на градуснике, тонометре, ростомере, весах, шприцах, пробирках для взятия анализов крови. Также в медицине очень много математических формул, например:
-для расчета пульсового давления;
-подбора линзы при замене хрусталика;
-во введении жидкости и электролитов больным с дегидратацией и мн. др.
Такая важная отрасль медицины, как хирургия также не может обойтись без математики. Все аппараты работают на компьютерных программах, составление которых без знания математики просто невозможно.
Без математики невозможно не только сделать лечебные и диагностические приборы, но и работать на них. Ведь все программы, на которых работают эти приборы, составляются для компьютера по предварительным расчётам.
На основе вышеизложенного можно сказать, что медицинская наука, конечно, не поддаётся формализации, но огромная эпизодическая роль математики в медицине несомненна. Все медицинские открытия должны опираться на численные соотношения. А методы теории вероятности (учёт статистики заболеваемости в зависимости от различных факторов) - вещь в медицине необходимая. В медицине без математики шагу не ступить. Численные соотношения, например, учёт дозы и периодичности приёма лекарств. Численный учёт сопутствующих факторов, таких как: возраст, физические параметры тела, иммунитет и пр.
2. Экспериментальная часть и анализ полученных результатов
Исследования проводились в Деяновском ФАПе при содействии фельдшера Чилеевой И.В.
Объекты исследования: ученики 7 класса.
Тема: Расчёт пульса
Этот способ доступен в любых условиях. Общий принцип таков: подсчитать пульс до нагрузки; дать определенную нагрузку в течении 3-х минут (20 приседаний); подсчитать пульс сразу после нагрузки; подсчитать пульс через
3 минуты после нагрузки. Если увеличение пульса составляет 35-50% от исходного, то нагрузка малая, если прирост 50-70%, то нагрузка средняя, если прирост 70-90%, то нагрузка высокая.
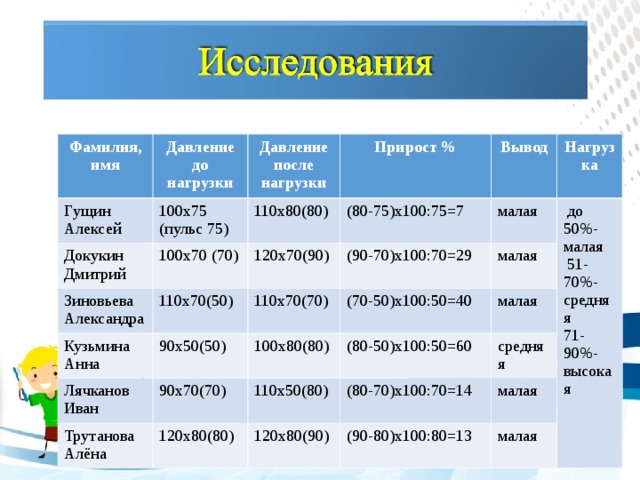
| Фамилия, имя | Давление до нагрузки | Давление после нагрузки | Прирост % | Вывод | Нагрузка |
| Гущин Алексей | 100х75 (пульс 75) | 110х80(80) | (80-75)х100:75=7 | малая | до 50%- малая 51-70%- средняя 71-90%- высокая |
| Докукин Дмитрий | 100х70 (70) | 120х70(90) | (90-70)х100:70=29 | малая |
| Зиновьева Александра | 110х70(50) | 110х70(70) | (70-50)х100:50=40 | малая |
| Кузьмина Анна | 90х50(50) | 100х80(80) | (80-50)х100:50=60 | средняя |
| Лячканов Иван | 90х70(70) | 110х50(80) | (80-70)х100:70=14 | малая |
| Трутанова Алёна | 120х80(80) | 120х80(90) | (90-80)х100:80=13 | малая |
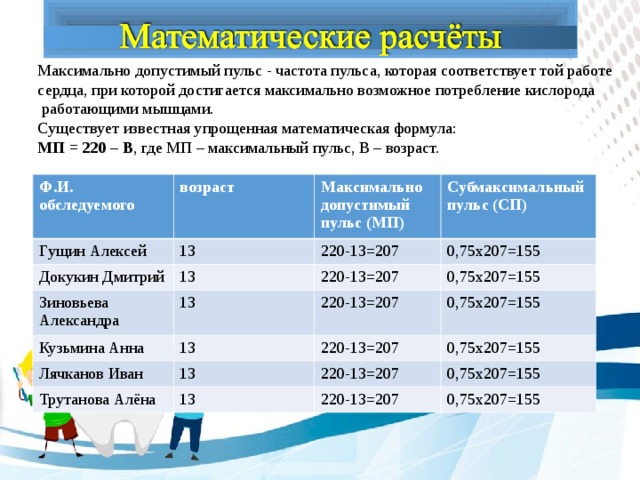
То есть, если 20 приседаний вызывают минимальный прирост пульса, то считать это хорошей тренирующей нагрузкой нецелесообразно. И наоборот, если пульс учащается, чуть ли не вдвое, это означает, что данная нагрузка высоковата. Максимально допустимый пульс - частота пульса, которая соответствует той работе сердца, при которой достигается максимально возможное потребление кислорода работающими мышцами.Существует известная упрощенная математическая формула:МП = 220 – В, где МП – максимальный пульс, В – возраст.
| Ф.И. исследуемого | Возраст | Максимально допустимый пульс (МП) | Субмаксимальный пульс (СП) (при нагрузке) |
| Гущин Алексей | 13 | 220-13=207 | 0,75х207=155 |
| Докукин Дмитрий | 13 | 220-13=207 | 0,75х207=155 |
| Зиновьева Александра | 13 | 220-13=207 | 0,75х207=155 |
| Кузьмина Анна | 13 | 220-13=207 | 0,75х207=155 |
| Лячканов Иван | 13 | 220-13=207 | 0,75х207=155 |
| Трутанова Алёна | 13 | 220-13=207 | 0,75х207=155 |
Расчёт субмаксимального пульса
Субмаксимальный пульс рассчитывается как 75% или 85% от максимального. СП = 0,75 х МП
Таким образом, максимальный эффект для здоровья мы получаем при нагрузке, соответствующей субмаксимальному пульсу.
То есть нагрузка должна давать пульс, не превышающий субмаксимальный уровень и уж тем более не приближаться к максимально допустимому уровню. В противном случае, наносится большой вред здоровью, а возможна и внезапная смерть.
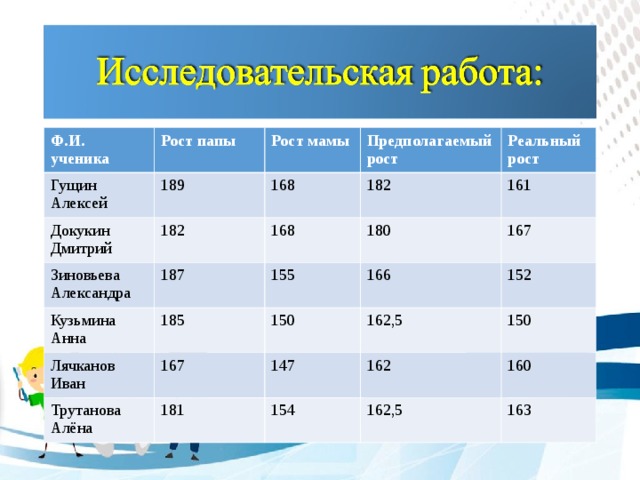
Следить за весом тела так же необходимо, как следить за пульсом или артериальным давлением. Вес зависит от роста человека.
| Ф.И. исследуемого | Рост папы | Рост мамы | Предполагаемый рост | Реальный рост |
| Гущин Алексей | 189 | 168 | 182 | 161 |
| Докукин Дмитрий | 182 | 168 | 180 | 167 |
| Зиновьева Александра | 187 | 155 | 166 | 152 |
| Кузьмина Анна | 185 | 150 | 162,5 | 150 |
| Лячканов Иван | 167 | 147 | 162 | 160 |
| Трутанова Алёна | 181 | 154 | 162,5 | 163 |
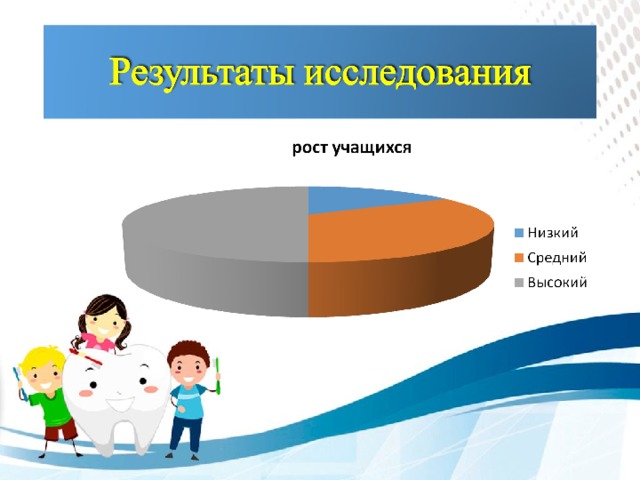
В ходе исследования получены следующие результаты: низкий рост-1 ученик, средний рост- 1 ученик, высокий рост- 4 ученика.
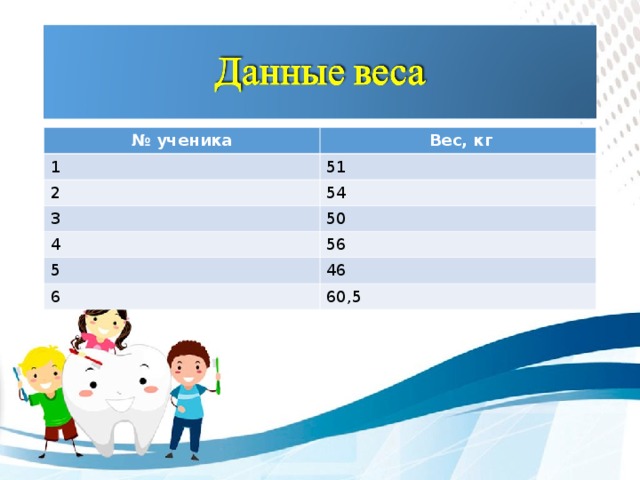
| Ф.И. исследуемого | Вес, кг |
| Гущин Алексей | 51 |
| Докукин Дмитрий | 54 |
| Зиновьева Александра | 50 |
| Кузьмина Анна | 56 |
| Лячканов Иван | 46 |
| Трутанова Алёна | 60,5 |
Результаты исследования: нормальный вес- 4 учащихся, выше нормы- 1 учащийся, ниже нормы- 1 учащийся.
3. Заключение
Итак, широкое использование математики в области медицины по существу только развивается, но оно может создать настоящую революцию во всей медицинской науке. Мы встречались с фельдшером Деяновского ФАПа Чилеевой И.В. они подтвердила, что каждый день в своей работе встречается с математическими расчетами и без математики обойтись в современной медицине невозможно. Хотя многие чисто математические расчеты сегодня выполняются современными компьютерами, которые выполняют их намного более эффективно, нежели человек. Но благодаря этому у врачей больше времени для выполнения их непосредственных обязанностей, которые требуют интуиции, здравого смысла, а также чувства сострадания, которых на сегодняшний день математика не может заменить.
В данной работе я представил вашему вниманию целый ряд практических примеров, которые наиболее ярко подтверждают актуальность использования математики в современной медицине. Суммируя всё написанное выше, можно с полной уверенностью утверждать, что это две сферы знаний, которые гармонично сочетаются друг с другом для выполнения поставленных целей.
4. Литература
Краснюк И.И. Фармацевтическая технология: Технология лекарств. форм. - М.: Академия, 2004
Шаталова Г.С. Философия здоровья. – М, 1997.
Алгоритм измерения веса и роста пациента
http://fb.ru/article/203920/algoritm-izmereniya-rosta-i-vesa-patsienta
4.Измерение артериального давления
http://med-tutorial.ru/m-lib/b/book/354254083/42
5.Википедия (свободная энциклопедия).
https://ru.wikipedia.org/wiki/Медицина
6. Значение математики в медицине
https://studopedia.org/9-138895.html
14