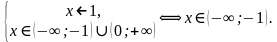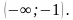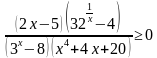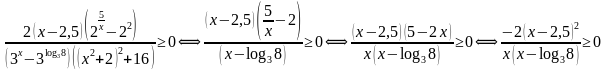МЕТОД РАЦИОНАЛИЗАЦИИ
при решении логарифмических и показательных неравенств
При решении неравенств методом интервалов вычисление значений функции в промежуточных точках может вызвать трудности вычислительного характера. С другой стороны, для рациональных функций такие вычисления несколько проще.
Чтобы расширить возможности применения метода интервалов при решении неравенств, используется метод рационализации неравенств, известный в математической литературе под другими названиями: метод декомпозиции; метод замены множителей.
Метод рационализации заключается в замене сложного выражения 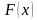 на более простое выражение
на более простое выражение 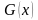 , при которой неравенство
, при которой неравенство 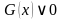 равносильно неравенству
равносильно неравенству 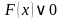 в области определения выражения
в области определения выражения 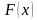 . В этом случае говорят, что выражение
. В этом случае говорят, что выражение 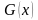 является рационализацией (или рационализирующим выражением) для выражения
является рационализацией (или рационализирующим выражением) для выражения 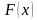 . Этот метод позволяет довольно сильно упростить решение и вычисления. Здесь символ
. Этот метод позволяет довольно сильно упростить решение и вычисления. Здесь символ 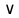 заменяет один из знаков
заменяет один из знаков 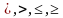 .
.
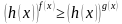
Если бы мы решали данное неравенство классическим способом, то оно было бы равносильно совокупности:
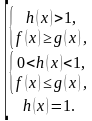
По методу рационализации данное неравенство равносильно системе:
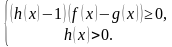 Покажем, что решения совокупности и системы совпадают.
Покажем, что решения совокупности и системы совпадают.
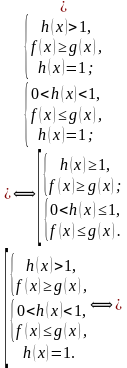
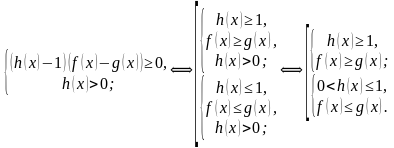
Решение совокупности и системы полностью совпадают.
Приведём примеры решения показательных неравенств.
1. Решить неравенство 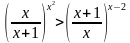
Используя метод рационализации, получаем систему неравенств:
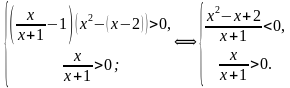
Так как 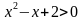 при любом значении
при любом значении 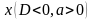 , то дробь
, то дробь 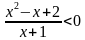 , если
, если
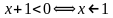 . Решая второе неравенство методом интервалов, находим:
. Решая второе неравенство методом интервалов, находим:
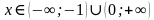 . Значит,
. Значит,
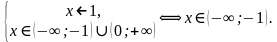
Ответ: 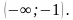
2. Решить неравенство 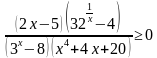
Преобразуем неравенство и применим метод рационализации:
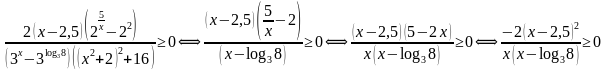
Решая последнее неравенство методом интервалов, находим:
Ответ:
3. Решить неравенство 
Преобразуем неравенство и применим метод рационализации:
4. Решить неравенство
Преобразуем неравенство и применим метод рационализации:
Ответ:
Заметим, что этот метод используется при решении неравенств с переменным основанием логарифма и позволяет решать неравенства такого вида без перехода к равносильной совокупности систем, решение которой является достаточно трудоёмким и требующим большого количества времени.
Если бы мы решали данное неравенство классическим способом, то оно было бы равносильно совокупности:
По методу рационализации данное неравенство равносильно системе:
Покажем, что решения совокупности и системы совпадают.
Решение совокупности и решение системы полностью совпадают.
Приведём примеры решения логарифмических неравенств.
1. Решить неравенство
Преобразуем неравенство и применим метод рационализации.
Ответ:
2. Решить неравенство
Применим метод рационализации.
Ответ: 
3. Решить неравенство
Применим метод рационализации.
Ответ: 
4. Решить неравенство
Применим метод рационализации.
Ответ: 
Если — многочлены, то метод рационализации позволяет перейти от показательного или логарифмического неравенства к рациональному, которое уже легко решается методом интервалов.
Если  – выражения с переменными, причём ; числа
– выражения с переменными, причём ; числа  – фиксированные,
– фиксированные,  , то выражения
, то выражения  и
и  имеют одинаковые знаки.
имеют одинаковые знаки.
При использовании метода рационализации, удобно помнить алгоритм.
Алгоритм метода рационализации.
Выписать условия, задающие ОДЗ исходного неравенства.
Привести исходное неравенство к стандартному виду.
Указать область допустимых значений для получившегося неравенства.
Заменить все выражения на рациональные (используя таблицу перехода к рациональным выражениям).
Решить полученное неравенство (как правило, методом интервалов).
Записать ответ полученного неравенства.
3







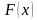 на более простое выражение
на более простое выражение 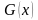 , при которой неравенство
, при которой неравенство 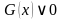 равносильно неравенству
равносильно неравенству 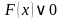 в области определения выражения
в области определения выражения 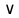 заменяет один из знаков
заменяет один из знаков 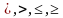 .
.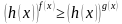
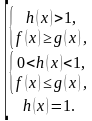
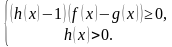 Покажем, что решения совокупности и системы совпадают.
Покажем, что решения совокупности и системы совпадают.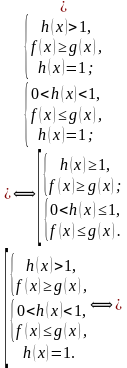
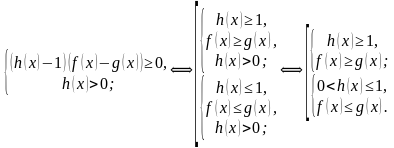
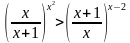
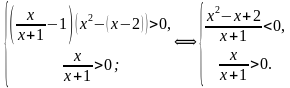
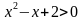 при любом значении
при любом значении 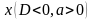 , то дробь
, то дробь 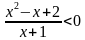 , если
, если 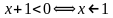 . Решая второе неравенство методом интервалов, находим:
. Решая второе неравенство методом интервалов, находим: 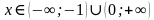 . Значит,
. Значит,