Тема: «Производная сложной функции»
Цели: 1) образовательная – сформировать понятие сложной функции, изучить алгоритм вычисления производной сложной функции, показать его применение при вычислении производных
2) развивающая – продолжить развитие умений логически и аргументировано рассуждать, используя обобщения, анализ, сравнение при изучении производной сложной функции
3) воспитательная – воспитывать наблюдательность в ходе отыскания математических зависимостей, продолжить формирование самооценки при осуществлении дифференцированного обучения, повышать интерес к математике
Тип урока: синтетический
Методы обучения: информационный, проблемный, частично-поисковый
Формы обучения: фронтальная, парная, индивидуальная
Оборудование: классная доска, мел, раздаточный материал к уроку, таблица производных
План урока:
Сообщение цели, задач урока и мотивации учебной деятельности
Проверка выполнения домашнего задания (фронтальная проверка, самоконтроль)
Подготовка к усвоению (изучению) нового учебного материала через повторение и актуализацию опорных знаний (проблемная ситуация, устный счет)
Изучение нового материала
Первичное осмысление и понимание нового материала
Закрепление новых знаний (самостоятельная работа – тест в двух вариантах, с дифференцированными заданиями)
Информация о домашнем задании, инструкция о его выполнении
Подведение итогов урока, рефлексия
Ход урока
1. Сообщение цели, задач и плана урока, мотивации учебной деятельности
- проверить подготовленность аудитории и готовность обучающихся к уроку, отметить отсутствующих.
- отметить, что на данном уроке продолжается работа по теме “Производная функции”
2. Проверка домашнего задания
- обучающиеся индивидуально проверяют свои ответы и ставят себе (самоконтроль) оценку в лист контроля. У каждого ученика имеется лист контроля, критерий оценки за домашнюю работу
- обратить внимание на правильное решение и правильное оформление решения домашнего примера.
3. Устный счет.
- каждый учащийся выходит к доске и записывает ответ к заранее подготовленным заданиям
4. Изучение нового материала
5. Первичное осмысление и понимание нового материала
- повторить алгоритм нахождения производной сложной функции;
- решить примеры
1) 
2) 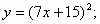
3) 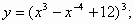
4) 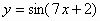 ;
;
5) 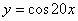 ;
;
6) 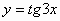 ;
;
7) 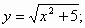
8) 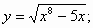
6. Закрепление новых знаний
Задания с тестами дифференцированные: примеры с № 1-3 оцениваются на “3”, до № 4 – на “4”, все пять примеров – на “5”.
Студенты решают в тетради и проверяют ответы друг у друга с помощью мультимедиа и ставят оценку друг другу (взаимоконтроль) в лист контроля.
Тест.
Вариант 1.
Найти производные функций. (А., В., С. – ответы)
| № | Задание | Ответы |
| А | В | С |
| 1 | 
| 
| 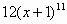
| 
|
| 2 | 
| 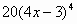
| 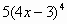
| 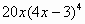
|
| 3 | 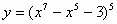
| 
| 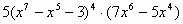
| 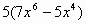
|
| 4 | 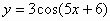
| 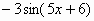
| 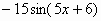
| 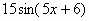
|
| 5 | 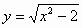
| 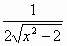
| 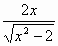
| 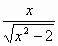
|
Вариант 2.
Найти производные функций. (А., В., С. – ответы)
| № | Задание | Ответы |
| А | В | С |
| 1 | 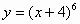
| 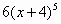
| 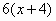
| 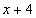
|
| 2 | 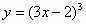
| 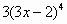
| 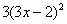
| 
|
| 3 | 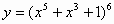
| 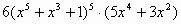
| 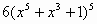
| 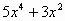
|
| 4 | 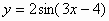
| 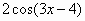
| 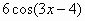
| 
|
| 5 | 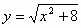
| 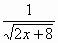
| 
| 
|
Информация о домашнем задании, инструкция о его выполнении
Подведение итогов урока, рефлексия
Самоанализ урока математики по теме:
«Производная сложной функции»
При отборе учебного материала для составления плана урока были учтены реальные учебные возможности студентов группы. Содержание урока соответствовало требованиям учебной программы и представлено общедидактическими принципами наглядности, доступности и последовательности.
Образовательная цель урока – сформировать понятие производной сложной функции и отработать алгоритм её вычисления в комплексе с развитием логического мышления, используя приёмы обобщения, анализа и сравнения.
Тип урока – синтетический. Структура занятия включает: актуализацию опорных знаний; изучение нового материала и его закрепление; повторение ранее пройденного. Занятие проводится как в форме изложения и объяснения преподавателем, так и в форме разнообразной работы студентов.
Методы обучения – информационный, проблемный, частично-поисковый. Преподавателем поставлена проблема – как найти производные функций( в последствии названными сложными). Для выхода из данной ситуации были рассмотрены различные примеры(таблица с примерами размещена на доске). Выяснили, что некоторые из функций состоят из двух подфункций – внутренней и внешней. В ходе рассуждений, анализируя и сравнивая, студенты сделали вывод, что такого вида функции называются сложными и составили алгоритм для её вычисления.
Используя карточки-памятки с этим алгоритмом организовано первичное осмысление и закрепление материала. Студенты повторили алгоритм и применяли его комментируя решение примеров из учебника. Под контролем преподавателя студенты справились с полученным заданием.
На следующем этапе закрепления студенты решали тесты с дифференцированными заданиями. После чего выполнили взаимопроверку по ответам с доски и выставили друг другу оценки по пятибалльной системе. Подвели итоги урока, разобрали инструкцию по выполнению домашнего задания.
В ходе урока развивались навыки работы с учебником, умение действовать по алгоритму, работать в парах, адекватность оценивания выполненных заданий.
На заключительном этапе внимание студентов было направлено на понимание того, что знания и умения по данной теме нужны для дальнейшей учебы и применения в профессиональной деятельности.
Все этапы урока выполнены. На каждом из них, работа строилась таким образом, чтобы студенты чувствовали себя полноценными участниками образовательного процесса. Деятельность студентов была направлена на решение поставленных задач и развитие самого себя.
Как преподаватель, свою задачу видела в том, чтобы вовлечь каждого студента в активную работу, создать условия для самореализации и уверенности в себе. В силу того, что в этой группе есть студенты со средними способностями, мало активны, то не всех студентов получилось вовлечь в качественную работу, у некоторых студентов имеются пробелы в знаниях. Это видно при выполнении дифференцированного теста. Таким студентам выданы варианты тестовых заданий, контрольные вопросы, назначены консультации.

















