Занятие 111. «Векторы в пространстве. Действия над векторами»
План занятия:
Понятие вектора.
Координаты точки в пространстве.
Построение точки в пространстве.
Понятие вектора.
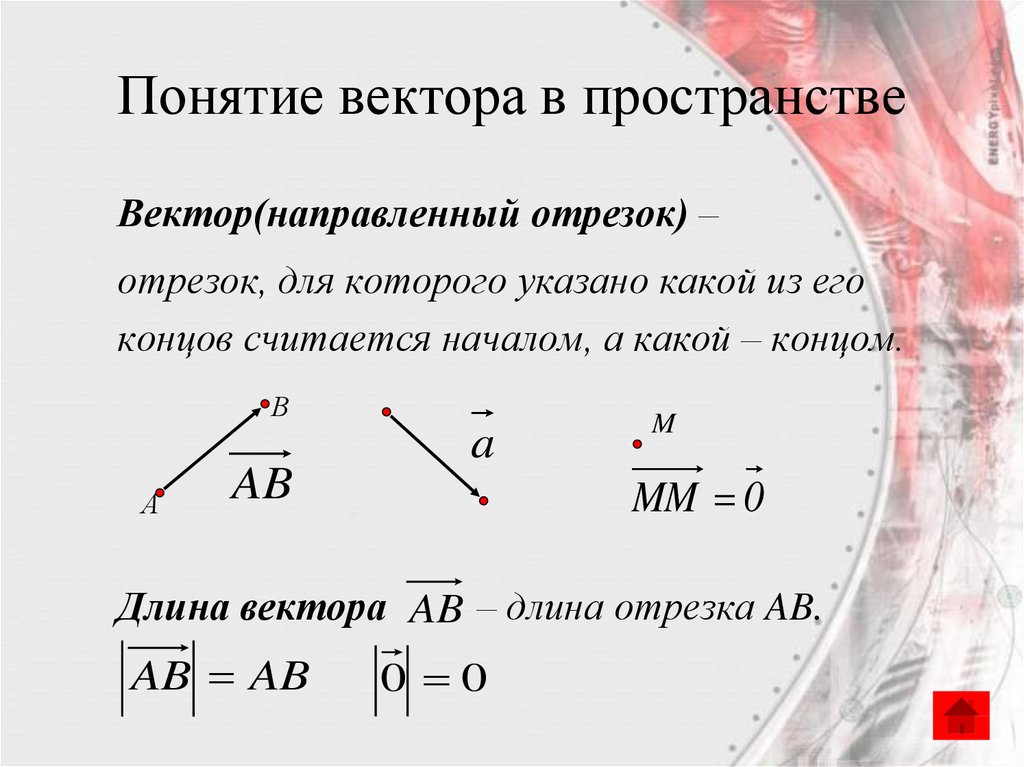
Вектором называется отрезок, для которого указано, какой из его концов считается началом, а какой - концом.
Любая точка пространства рассматривается как нулевой вектор.
2. Координаты точки и вектора в пространстве.
Любая точка М(x; y; z) в пространстве имеет 3 координаты: х-абсцисса, у-ордината, z-аппликата.
Любой вектор 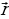 ={х; у; z} или
={х; у; z} или 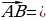 { х2 – х1, у2 – у1, z2 – z1} в пространстве также имеет 3 координаты:
{ х2 – х1, у2 – у1, z2 – z1} в пространстве также имеет 3 координаты:
х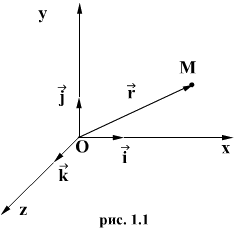 - абсцисса, у- ордината, z- аппликата.
- абсцисса, у- ордината, z- аппликата.
Радиус-вектором называют вектор, проведённый из начала координат в произвольную точку пространства. Радиус-вектор имеет координаты точки, в которую он проведён.
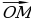 =
=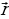 ={х; у; z}
={х; у; z}
Координаты вектора 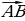 выражаются через координаты его начала А (х1; у1; z1) и конца В(х2; у2; z2):
выражаются через координаты его начала А (х1; у1; z1) и конца В(х2; у2; z2):
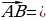 { х2 – х1, у2 – у1, z2 – z1}.
{ х2 – х1, у2 – у1, z2 – z1}.
Правило. Для определения координат вектора АВ нужно от координат конца вектора вычесть координаты начала.
Координаты равных векторов равны.
Длина вектора (модуль вектора) 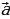 (х; у; z) вычисляется по формуле:
(х; у; z) вычисляется по формуле: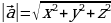
3. Действия с векторами в координатной форме:
Правило. Суммой (разностью) векторов 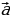 (х1; у1; z1) и
(х1; у1; z1) и 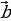 (х2; у2; z2) называется вектор
(х2; у2; z2) называется вектор 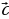 =
= 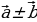 , координаты которого равны сумме (разности) соответствующих координат этих векторов:
, координаты которого равны сумме (разности) соответствующих координат этих векторов:
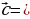 (х1
(х1 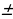 х2; у1
х2; у1 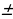 у2; z1
у2; z1 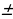 z2).
z2).
Правило. Произведением вектора 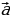 (х; у; z) на число k называется вектор
(х; у; z) на число k называется вектор
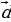 =k
=k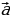 , координаты которого равны произведению числа k на координаты вектора
, координаты которого равны произведению числа k на координаты вектора 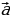 :
:
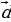 =(kх; kу; kz).
=(kх; kу; kz).
П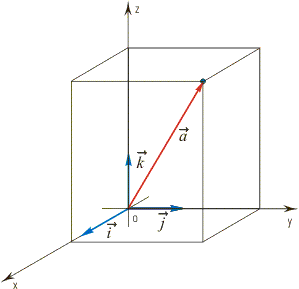 равило. Построение радиус-вектора в пространстве
равило. Построение радиус-вектора в пространстве
Для построения радиус-вектора в пространстве необходимо:
1) Построить прямоугольную систему координат в пространстве Охуz.
2) Отложить первые две координаты конца вектора на соответствующих осях и провести их проекции;
3) Выполнить параллельный перенос третьей координаты в точку пересечения проекций;
4) Соединить полученную точку с началом координат и обозначить искомый вектор.
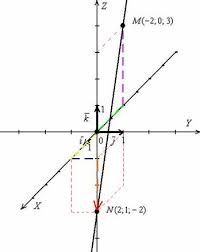 Правило. Построение вектора MN в пространстве
Правило. Построение вектора MN в пространстве
Для построения вектора MN в пространстве необходимо:
1) Построить прямоугольную систему координат в пространстве Охуz.
2) По правилу построить 2 точки - точку начала вектора M(-2;0;3) и точку конца N(2;1; -2).
3) Соединить полученные точки и обозначить искомый вектор.
Задание для самостоятельного выполнения
Задание 1. Сделать краткий конспект данной темы.
Задание 2. Выучить все формулировки определений и теорем.
Задание 3. Рассмотреть решение задач.
Задание 4. Решить задачи.
Задача 1. Найдите координаты вектора 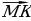 , если М(10; -4; 2) и К(16; 2 -5).
, если М(10; -4; 2) и К(16; 2 -5).
Задача 2. Найдите длину вектора 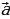 ( - 5; 1; 2).
( - 5; 1; 2).
Задача 3. Найдите сумму векторов 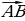 и
и 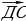 , если А(2; 3; -1), С(3; -2; 0), В (3,6,0), Д (-2,5,-4)
, если А(2; 3; -1), С(3; -2; 0), В (3,6,0), Д (-2,5,-4)
Задача 4. Найдите разность векторов 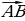 и
и 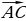 , если В(3; 7; 10), С(1; 9; -6), А(-6,0,1)
, если В(3; 7; 10), С(1; 9; -6), А(-6,0,1)
Выполненные задания и вопросы по выполнению работ отправить на адрес электронной почты преподавателя: [email protected]. Имя файла – фамилия студента и номер занятия. (например, Петров-111)








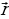 ={х; у; z} или
={х; у; z} или 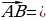 { х2 – х1, у2 – у1, z2 – z1} в пространстве также имеет 3 координаты:
{ х2 – х1, у2 – у1, z2 – z1} в пространстве также имеет 3 координаты:  - абсцисса, у- ордината, z- аппликата.
- абсцисса, у- ордината, z- аппликата. 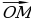 =
=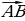 выражаются через координаты его начала А (х1; у1; z1) и конца В(х2; у2; z2):
выражаются через координаты его начала А (х1; у1; z1) и конца В(х2; у2; z2):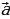 (х; у; z) вычисляется по формуле:
(х; у; z) вычисляется по формуле: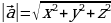
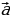 (х1; у1; z1) и
(х1; у1; z1) и 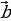 (х2; у2; z2) называется вектор
(х2; у2; z2) называется вектор 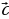 =
= 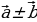 , координаты которого равны сумме (разности) соответствующих координат этих векторов:
, координаты которого равны сумме (разности) соответствующих координат этих векторов: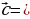 (х1
(х1 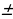 х2; у1
х2; у1 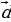 =k
=k равило. Построение радиус-вектора в пространстве
равило. Построение радиус-вектора в пространстве Правило. Построение вектора MN в пространстве
Правило. Построение вектора MN в пространстве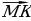 , если М(10; -4; 2) и К(16; 2 -5).
, если М(10; -4; 2) и К(16; 2 -5). 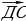 , если А(2; 3; -1), С(3; -2; 0), В (3,6,0), Д (-2,5,-4)
, если А(2; 3; -1), С(3; -2; 0), В (3,6,0), Д (-2,5,-4)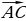 , если В(3; 7; 10), С(1; 9; -6), А(-6,0,1)
, если В(3; 7; 10), С(1; 9; -6), А(-6,0,1)









