Просмотр содержимого документа
«Найти наименьшее значение функции с е в степени х.»
Задание №11 ЕГЭ по математике профильного уровня.
Условие: Найдите наименьшее значение функции у=е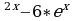 +7 на промежутке
+7 на промежутке 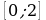 .
.
Решение: Как мы знаем, при решении задач №11 профильного уровня мы всегда находим производные. Сначала рассмотрим, из чего же состоит наша функция у=е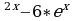 +7? Это сумма трёх слагаемых. Производная суммы равна сумме производных. Формула: 2/
+7? Это сумма трёх слагаемых. Производная суммы равна сумме производных. Формула: 2/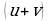
 =
= 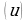
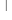 +
+ 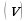
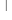
Следовательно, производная искомой функции
у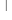 = (е
= (е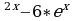 +7
+7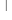 =
= 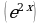
 -
- 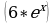
 +7
+7 =
=
( Найдём производную сложной функции:
(е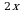 )
)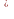 =е
=е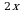 * (2х)
* (2х)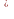 =2* е
=2* е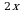 =2*
=2*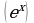
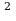 ,
,
е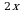 можно записать как
можно записать как 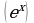
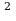 по формуле
по формуле 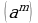
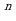 =
= 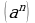
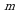 )
)
= 2*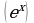
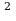 - 6* е
- 6* е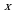 + 0 = (Теперь выносим е
+ 0 = (Теперь выносим е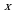 за скобки) = е
за скобки) = е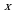 (2* е
(2* е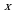 - 6)
- 6)
Дальше производную функции приравняем к нулю, чтобы найти корни уравнения у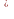 =0.
=0.
е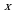 *(2* е
*(2* е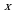 - 6)=0,
- 6)=0,
е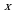 =0 или 2* е
=0 или 2* е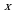 - 6 =0.
- 6 =0.
2* е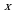 - 6 =0
- 6 =0
е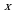 =3
=3
Самое главное, что нам сейчас не нужно будет находить х! Чтобы найти наименьшее значение функции, в функцию у=е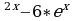 +7 вместо е
+7 вместо е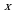 ставим числа 0 и 3. Итак, сначала ставим 0:
ставим числа 0 и 3. Итак, сначала ставим 0:
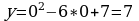
у= 3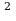 -6*3+7= 9-18+7= - 2.
-6*3+7= 9-18+7= - 2.
Задача ещё до конца не решена, так как у нас есть концы отрезка 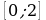 , поэтому находим значения функции у при значениях 0 и 2.
, поэтому находим значения функции у при значениях 0 и 2.
у(0)= е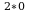 - 6* е
- 6* е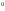 +7= е
+7= е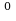 - 6* 1+7= 1-6+7=2,
- 6* 1+7= 1-6+7=2,
у(2)= е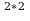 - 6* е
- 6* е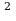 +7=е
+7=е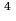 -6* е
-6* е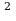 +7.
+7.
У нас получились три красивых ответа -2, 2 и 7. Среди них выбираем ответ: наименьшее значение функции 1/ у=е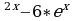 +7 на промежутке
+7 на промежутке 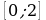 это число -2.
это число -2.
Ответ: -2.







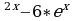 +7 на промежутке
+7 на промежутке 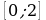 .
.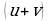
 =
= 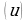
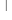 +
+ 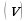
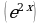
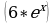
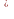 +7
+7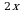 )
)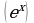
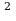 ,
,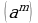
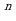 =
= 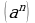
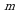 )
)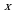 + 0 = (Теперь выносим е
+ 0 = (Теперь выносим е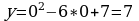
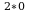 - 6* е
- 6* е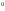 +7= е
+7= е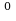 - 6* 1+7= 1-6+7=2,
- 6* 1+7= 1-6+7=2,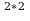 - 6* е
- 6* е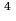 -6* е
-6* е









