Дата: 28.11.2019 года
Класс: 9 «Б»
Предмет: алгебра
Тема урока: Решение задач на тему «Арифметическая прогрессия. Формула n-го члена арифметической прогрессии».
Цель урока: Сформировать у учащихся понятие арифметической прогрессии и научить применять формулы к решению практических задач. Закрепление понятий прогрессия, член прогрессии, разность прогрессии, сумма. Отработать умения и навыки применения формул n-го члена прогрессии, суммы n - первых членов, свойств членов прогрессии.
Задачи урока:
Образовательные: Проверки и коррекции знаний, умений и навыков учащихся, связанных с решением задач по теме «Арифметическая прогрессия»; решения задач с использованием межпредметных связей;
Развивающие: Развитие внимания, умения анализировать, делать выводы, решать проблему. Развитие умения строить логическую цепочку в своих рассуждениях при решении стандартных задач и задач повышенного уровня. Развитие навыки само и взаимоконтроль.
Воспитательные: Воспитывать доверие учащихся друг к другу при взаимопроверке, сотрудничество и коммуникативность при групповой работе. Воспитание у учащихся трудолюбия, усидчивости, а так же сознательной дисциплины на уроке. Повышение интереса к изучению математики.
Оборудование: ноутбук, презентация, раздаточные материалы и т.д.
Формы организации урока: фронтальная, индивидуальная, в парах, групповая.
Тип урока: обобщения и систематизации знаний.
Метод обучения: наглядный (презентация), словесный (беседа, объяснение, диалог), практический.
Ход урока:
1.Организационный момент.
Приветствие учащихся, определение отсутствующих, проверка готовности учащихся к уроку, организация внимания.
2.Сообщение темы и целей урока.
Давайте вместе с вами определим цели урока.
На уроке мы с вами повторим и обобщим все знания о арифметической прогрессии, повторим формулы, по решаем задачи на нахождение н-го члена и суммы н- первых членов арифметической прогрессии. Рассмотрим задания, встречающеееся в ОГЭ по данной теме
Ваша главная задача – быть внимательными, активными, находчивыми, а главное – трудолюбивыми .
3.Актуализация знаний. Повторение теории и формул. (тест с выбором ответа)
Теоретический тест. 1 вариант
1). Для вычисления суммы n-членов арифметической прогрессии используется формула
А). б).
б). в).
в). г).
г).
2). Арифметическая прогрессия это-
А). последовательность чисел, в которой каждое число, начиная со второго, получается из предыдущего умножением этого числа на постоянное число.
Б). последовательность чисел, в которой каждое число, начиная со второго, получается из предыдущего добавлением к н
 исла.
исла.
3). Для вычисления второго члена прогрессии прогрессии применим формулу (d-разность прогрессии)
А). б).
б). в).
в). г).
г).
4). Свойство членов арифметической прогрессии
А). Каждый член арифметической прогрессии, начиная со второго равен среднему арифметическому двух его соседних членов.
Б). Каждый член арифметической прогрессии, равен среднему арифметическому двух его соседних членов.
В). Каждый член арифметической прогрессии, начиняя со второго равен среднему арифметическому разности этой прогрессии и самого числа
5). Из приведенных ниже формул выбрать формулу n-члена прогрессии
А). б).
б). б).
б). б).
б).
Теоретический тест.2 вариант
1). Для вычисления суммы n-членов арифметической прогрессии используется формула
А). б).
б). в).
в). г).
г).
2). Арифметическая прогрессия это-
А). последовательность чисел, в которой каждое число, начиная со второго, получается из предыдущего умножением этого числа на постоянное число.
Б) Каждый член арифметической прогрессии, начиняя со второго равен среднему арифметическому разности этой прогрессии и самого числа
В). последовательность чисел, в которой каждое число, начиная со второго, получается из предыдущего добавлением к н
3). Для вычисления третьего члена прогрессии применим формулу
А). б).
б). в).
в). г).
г).
4). Свойство членов арифметической прогрессии
А). Каждый член арифметической прогрессии, начиняя со второго равен среднему арифметическому разности этой прогрессии и самого числа
Б). Каждый член арифметической прогрессии, начиная со второго равен среднему арифметическому двух его соседних членов.
В). Каждый член арифметической прогрессии, равен среднему арифметическому двух его соседних членов.
5). Из приведенных ниже формул выбрать формулу n-члена прогрессии
А). б).
б). б).
б). б).
б).
4. Проверка умений учащихся самостоятельно применять знания в стандартных ситуациях. Установить соответствие между заданием и ответу к ниму.

5. Применение умений при ешении более сложных заданиях.
Более подготовленные учащиеся решают задания «найди ошибку», «слабые» учащие применение знаний для нахождение суммы членов и n-лагаемых.

1 вариант
Заполните таблицу
| a 1 | d | n | a n | S n |
| 8 | 3 | 3 |
|
|
| 14 | 5 | 10 |
|
|
| 4 | 3 | 6 |
|
|
| 5 | -7 | 5 |
|
|
| 84 | -4 | 8 |
|
|
2 вариант
Заполните таблицу
| a 1 | d | n | a n | S n |
| 5 | -7 | 5 |
|
|
| 7 | -8 | 10 |
|
|
| 96 | -4 | 4 |
|
|
| 8 | 3 | 8 |
|
|
| 4 | 2 | 6 |
|
|
Ответы:
1 вариант
Заполните таблицу
| a 1 | d | n | a n | S n |
| 8 | 3 | 3 | 14 | 33 |
| 14 | 5 | 10 | 59 | 365 |
| 4 | 3 | 6 | 19 | 69 |
| 5 | -7 | 5 | -23 | -45 |
| 84 | -4 | 8 | 56 | 560 |
2 вариант
Заполните таблицу
| a 1 | d | n | a n | S n |
| 5 | -7 | 5 | -23 | -45 |
| 7 | -8 | 10 | 79 | 430 |
| 96 | -4 | 4 | 84 | 360 |
| 8 | 3 | 8 | 29 | 148 |
| 4 | 2 | 6 | 14 | 54 |
6.Физминутка.
7. Проверка умений учащихся применять знания в нестандартных ситуациях.
Решение задач практической направленности
Зная эти формулы, можно решить много интересных задач литературного, исторического и практического содержания.
Задача 1.
При хранении бревен строевого леса их укладывают так, как показано на рисунке. Сколько бревен находится в одной кладке, если в ее основание положить 12 бревен?

Решение:

Ответ: 78 бревен в одной кладке.
Задача 2.
"Свободно падающее тело проходит в первую секунду 4,9 м, а в каждую следующую секунду на 9,8 м больше, чем в предыдущую. Найдите глубину шахты, если свободно падающее тело достигло дна шахты через 5 секунд после начала падения".
Решение:

Ответ: глубина шахты 122,5 м.
Задача 3.
Родители ко Дню рождения своего сына Андрея решили купить и обновить ему мобильный телефон. Для этого они в первый месяц отложили 1500 тысячи рублей, а в каждый последующий месяц они откладывали на 500 рублей больше, чем в предыдущий.
Какая сумма будет у родителей Андрея через 10 месяцев?
Решение:
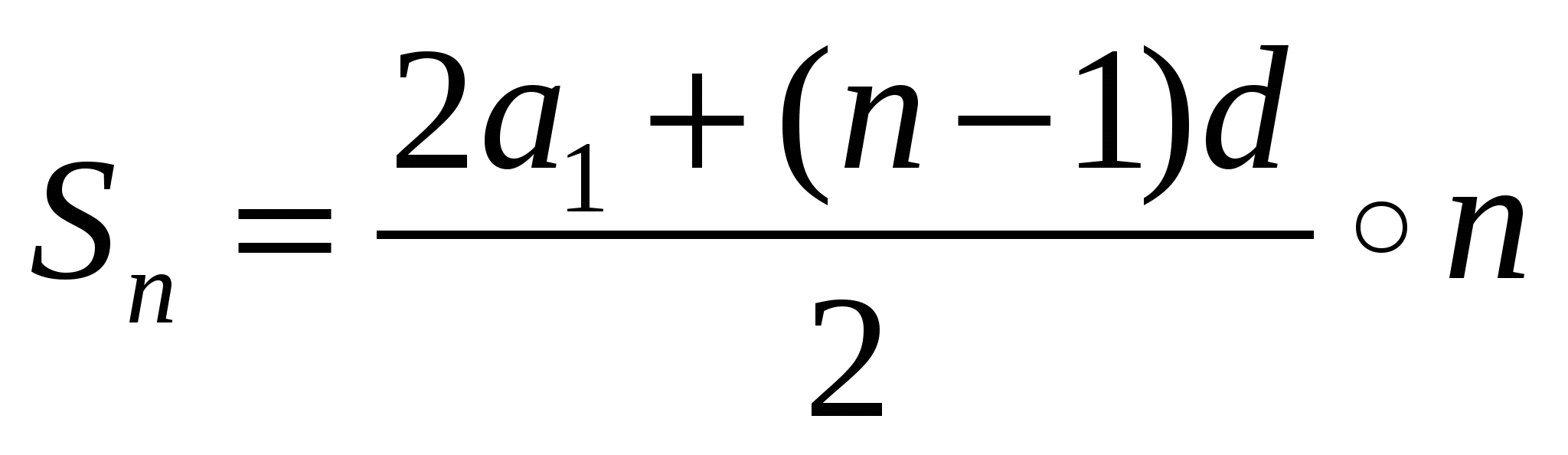



Ответ: 37500 рублей
8.Домашнее задание.
1).В первом ряду кинозала 30 мест, а в каждом следующем на 2 места больше, чем в предыдущем. Сколько мест в ряду с номером 50?
2).Вася решил сделать лестницу так, чтобы нижняя ступенька была равна 50 см, каждая следующая из 12 ступенек на 2 см короче. Какова длина самой верхней ступеньки?
3). Предприятие поставило себе цель выпускать каждый год на 15 единиц продукции больше, чем в предыдущий. Сколько единиц продукции произведёт предприятие за 13 лет, начиная с 8-го года, если в первый год было произведено 50 единиц продукции?
4). Гусеница проползла за первую минуту 39 см, а за каждую следующую минуту на 2 см меньше, чем в предыдущую. Через сколько минут она проползёт 4 м?
5). Альпинисты в первый день восхождения поднялись на высоту 1400 м, а затем каждый следующий день поднимались на высоту на 100 м меньше, чем в предыдущий. За сколько дней они покорили высоту 5000 м?
10.Итог урока. Оценивание.
Рефлексия.
Синквейн. (красивое многоточие)
Пишем синквейн (от англ. «путь мысли»)
Правила написания синквейна:
Одно слово. Существительное или местоимение, обозначающее предмет, о котором идет речь.
Два слова. Прилагательные или причастия, описывающие признаки и свойства выбранного предмета.
Три слова. Глаголы, описывающие совершаемые предметом или объектом действия.
Фраза из четырех слов. Выражает личное отношение автора к предмету или объекту.
Одно слово. Характеризует суть предмета или объекта.
Оценивание.
1).А я знаю? (5 баллов)
2).Умею ли я? (5 баллов)
3).Смогу ли я? (5 баллов)
4).Я могу все! (3 балла)
Всего: 18 баллов
9-11 баллов-»Мне надо поработать»
12-15 баллов «Я очень старался»
16-18 баллов –»Я такой молодец»
|
Карточка №1 Задана арифметическая прогрессия, где первый член равен 4, второй член равен 6. Найти разность арифметической прогрессии. 
|
|
Карточка №2 Задана арифметическая прогрессия, где первый член равен 4, второй член равен 6. Найти разность арифметической прогрессии. 
|
|
Карточка №3 Найдите третий член арифметической прогрессии  |
|
Карточка №4 Найдите третий член арифметической прогрессии  |
|
Карточка №5 Задана арифметическая прогрессия, где первый член равен 1, а разность равен 4. Найти десятый член арифметической прогрессии. 
|
|
Карточка №6 Задана арифметическая прогрессия, где первый член равен 1, а разность равен 4. Найти десятый член арифметической прогрессии. 
|
| Карточка №7 Задана арифметическая прогрессия, где пятый и десятый члены равны соответственно 38 и 23. Найти пятнадцатый член прогрессии и сумму ее десяти первых членов. 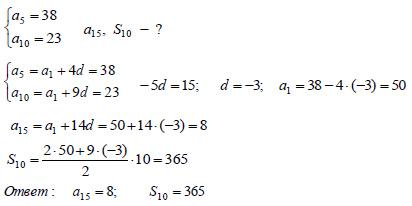
|
|
Карточка №8 Найти число  членов арифметической прогрессии 5,14,23,..., членов арифметической прогрессии 5,14,23,..., , если ее , если ее  -ый член -ый член равен 239. 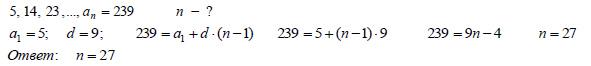
|
1 вариант
Заполните таблицу
| a 1 | d | n | a n | S n |
| 8 | 3 | 33 | 104 | 
|
| 14 | 5 | 100 |
|
|
| 4 | 3 | 33 |
|
|
Например:
а1 = 8, d = 3, n = 33, аn = ? Sn = ?
а33 = а1 + 32d = 8 + 32  3 = 8 + 96 = 104
3 = 8 + 96 = 104
S33 = 
 =
=
2 вариант
Заполните таблицу
| a 1 | d | n | a n | S n |
| 5 | -7 | 25 | -163 | 
|
| 7 | -8 | 50 |
|
|
| 96 | -4 | 24 |
|
|
Например:
а1 = 5, d = -7, n = 25, аn = ? Sn = ?
а25 = а1 + 24d = 5 + 24  (-7) = 5 + (-168) = -163
(-7) = 5 + (-168) = -163
S25 = 
 =
=
1 вариант
Заполните таблицу
| a 1 | d | n | a n | S n |
| 8 | 3 | 33 | 104 | 
|
| 14 | 5 | 100 |
|
|
| 4 | 3 | 33 |
|
|
Например:
а1 = 8, d = 3, n = 33, аn = ? Sn = ?
а33 = а1 + 32d = 8 + 32  3 = 8 + 96 = 104
3 = 8 + 96 = 104
S33 = 
 =
=
2 вариант
Заполните таблицу
| a 1 | d | n | a n | S n |
| 5 | -7 | 25 | -163 | 
|
| 7 | -8 | 50 |
|
|
| 96 | -4 | 24 |
|
|
Например:
а1 = 5, d = -7, n = 25, аn = ? Sn = ?
а25 = а1 + 24d = 5 + 24  (-7) = 5 + (-168) = -163
(-7) = 5 + (-168) = -163
S25 = 
 =
=
Тест по теме «Арифметическая и геометрическая прогрессии»
9 класс.
1 вариант
1. - арифметическая прогрессия, . Найдите .
а) -1; б) 1; в) 7; г) 9; д) 11
2. - арифметическая прогрессия, . Найдите .
а) -4; б) -2; в) -1; г) 2; д) 5
3.Найдите сумму третьего и седьмого членов арифметической прогрессии,
заданной формулой
а) 11; б) 13; в) 15; г) 17; д) 19
4. - арифметическая прогрессия, . Найдите .
а) -5; б) 2; в) 4; г) 5; д) 8
5.Найдите сумму десяти первых членов арифметической прогрессии
-1; 2; 5;…
а) 120; б) 122; в) 125; г) 127; д) 130
Тест по теме «Арифметическая и геометрическая прогрессии»
9 класс.
2 вариант
1. - арифметическая прогрессия, . Найдите .
а) -9; б) -7; в) -1; г) 1; д) 3
2. - арифметическая прогрессия, . Найдите .
а) -2; б) -1; в) 1; г) 2; д) 3
3.Найдите сумму третьего и седьмого членов арифметической прогрессии,
заданной формулой
а)- 11; б) -9; в) -7; г) -5; д) -3
4. - арифметическая прогрессия, . Найдите .
а) -4; б) -2; в) 0; г) 2; д) 4
5.Найдите сумму десяти первых членов арифметической прогрессии
5; 2; -1;…
а) -120; б) -115; в) -112; г) -110; д) -85





 б).
б). в).
в). г).
г).


 б).
б). в).
в). г).
г).
 б).
б). б).
б). б).
б).
 б).
б). в).
в). г).
г). б).
б). в).
в). г).
г).






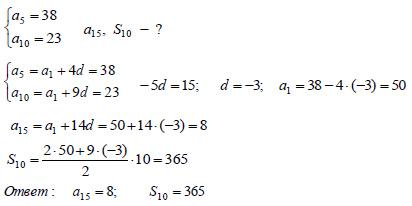

 3 = 8 + 96 = 104
3 = 8 + 96 = 104




























