Государственное учреждение образования
«Средняя школа №6 г. Жодино»
ОПИСАНИЕ ОПЫТА ПЕДАГОГИЧЕСКОЙ ДЕЯТЕЛЬНОСТИ
«РЕШЕНИЕ ТЕКСТОВЫХ ЗАДАЧ
ПУТЁМ ИСПОЛЬЗОВАНИЯ МОДЕЛИРОВАНИЯ»
Клыга Ольга Анатольевна,
учитель начальных классов
Информационный блок
Название темы опыта
Решение текстовых задач путём использования моделирования. Актуальность опыта
Умение решать текстовые задачи, была и будет одна из серьёзных проблем у учащихся школы. Анализируя методическую литературу, знакомясь с опытом работы других учителей по этой теме, используя свой опыт работы, определила, что решение большого количества однотипных задач способствует умению решать, но не приводит к формированию умения анализировать и решать задачи всех видов.
Помочь ученику преодолеть неизбежно возникающие трудности при решении текстовых задач может приём моделирования описанных в ней явлений и процессов.
Цель опыта – повышение эффективности обучения младших школьников решению текстовых задач путём моделирования.
Задачи опыта:
разработать комплекс заданий по выделению величин и их отношений в задачах;
определить последовательность освоения действия моделирования учащимися при решении задач;
определить эффективность обучения решению текстовых задач, используя моделирование.
Длительность работы над опытом
Продолжительность работы по теме моего опыта составляет 3,5 года и охватывает период с Ι по ΙV класс.
Описание технологии опыта
Ведущая идея опыта. Научить учащихся решать текстовые задачи посредством моделирования.
Научно-методическое обоснование опыта. На необходимость использования моделирования в учебной деятельности указали в своих работах психологи П.Я. Гальперин, В.В. Давыдов, Л.В. Занков, Н.И. Непомнящая и др. Для раскрытия сущности моделирования рассмотрим сначала понятие «модель». Слово «модель» в переводе с французского означает «образец» [2].
В математике под моделью понимают любую совокупность абстрактных объектов, свойства которых и отношения, между которым удовлетворяют основным положениям (аксиомам), служащим тем самым совместным (неявным) определение такой совокупности [1]. Математической моделью является описание реальной ситуации на языке математических понятий, формул и отношений. В ходе решения конкретной задачи строится «своя» математическая модель: уравнение или их система, диаграмма или график, изображение отношений между объектами при помощи кругов Эйлера. В качестве модели могут выступать изображения, описания, схемы, чертежи, графики, планы и т.п.
Основными принципами построения математической модели являются следующие:
1) модель должна отражать особые (в данном случае количественные) отношения реальной действительности;
2) модель должна замещать соответствующие реальные объекты, явления, процессы, ради которых она была создана;
3) модель, отображая структуру исследуемого объекта, процесса, ситуации, способна замещать его так, чтобы ее изучение давало новую информацию об этом объекте, ситуации и т.д.
По видам средств, используемых для построения, все модели можно разделить на схематизированные и знаковые.
Схематизированные модели делятся на вещественные и графические.
Вещественные (предметные) модели обеспечивают физическое действие с предметами. Они могут строиться из каких-либо предметов (пуговиц, спичек, бумажных полосок и т.д.). К этому виду моделей относят и мысленное воссоздание реальной ситуации изучаемого явления.
Графическими моделями являются рисунок, условный рисунок, чертеж, схематический чертеж (схема).
Знаковые модели могут быть выполнены как на естественном, так и на математическом языке. К знаковым моделям, выполненным на естественном языке, относят краткую запись текстовых задач, таблицы. Знаковыми моделями, выполненными на математическом языке, являются формулы, выражения, уравнения и их системы.
Для того чтобы модель как наглядно-практическое средство познания выполняла свою функцию, она должна соответствовать определенным требованиям [4]:
– четко отражать основные свойства и отношения, которые являются объектом познания, быть по структуре аналогичной объекту;
– быть простой для восприятия и доступной для создания и действий с ней;
– ярко и отчетливо передавать те свойства и отношения, которые должны быть освоены с ее помощью.
Сущность опыта. В работе над задачами я уделяю большое внимание построению схематических и символических моделей, а также умению младших школьников работать с отрезками, графически моделировать с их помощью текстовую задачу, ставить вопрос, определять алгоритм решения и поиска ответа. Чтобы научить учащихся самим создавать модели задач, необходимо их подготовить. Поэтому работа строится поэтапно:
I этап: подготовительная работа (подготовка учащихся к освоению действия моделирования);
II этап: обучение младших школьников моделированию текстовых задач;
III этап: закрепление у учащихся умения решать задачи с помощью моделирования.
I этап. Подготовительная работа
Подготовительную работу направляю на выполнение учащимися предметных действий. Отображая эти действия графически, сначала в виде рисунка, затем в виде модели, школьники в дальнейшем подходят к знаково-символической форме: равенству, формуле и так далее. Прежде чем представить задачу в виде модели, необходимо ознакомиться с ее содержанием.
При решении текстовой задачи содержание текста нужно перевести учащимся на математический язык. В этом случае необходимо выявление «математического ядра» задачи. Для этого я совместно с учащимися выделяла величины и отношения между ними, которые заключены, как говорят дети, в «главных» словах и числах (буквах)». Договаривались подчеркивать слова карандашом в книге и цветным мелком на доске. Вопрос задачи всегда выделяется особо – это цель наших действий. Например: На полке было 6 книг. Витя поставил ещё 2 книги. Сколько книг стало на полке?
Таким образом, исключение части слов не повлияло на математическую модель задачи, то есть учащиеся совершенно безболезненно смогли понять и, следовательно, решить данную задачу.
Для отработки умения выделять величины и отношения между ними, умения находить младшими школьниками опорные слова в практике я использую различные задания (Приложение 1).
С целью проверки умения учащимися находить в текстовой задаче величины и отношения между ними, умения самостоятельно дополнять условие задачи числовыми данными, умения составить рисунок к задаче, умения устанавливать связи между данными и искомыми числами и на этой основе выбирать соответствующее арифметическое действие провожу проверочную работу (Приложение 2). Хорошая результативность выполнения проверочной работы показывает, что можно приступать к следующему этапу.
II этап. Обучение младших школьников моделированию текстовых задач
После ознакомления с содержанием задачи приступаем с учащимися к её моделированию. Обучение моделированию веду целенаправленно, соблюдая ряд условий:
• применяю метод моделирования при изучении математических понятий;
• веду работу по усвоению знаково-символического языка, на котором строится модель;
• систематически провожу работу по освоению моделей тех отношений, которые рассматриваются в задачах;
• чтобы решать задачи самостоятельно школьник должен освоить различные виды моделей, обучаю способам выбора нужной модели, переходу от одной модели к другой.
Особенностью предметного моделирования простых текстовых задач является использование предметов, замещающих образец. Это могут быть полоски бумаги, геометрические фигуры и т.д. Особенности графического моделирования простых текстовых задач в том, что они строятся как частные случаи отношения величин: величины в задаче находятся в отношении целого и частей, что наглядно показывается в схеме.
Моделирование в виде схемы использую при решении задач, в которых даны отношения значений величин («больше», «меньше», «столько же»). Задачи, связанные с движением, моделирую с помощью чертежа, диаграммы или графика.
Наряду со схематическим моделированием, начиная с первого класса, использую и знаковое моделирование – это краткая запись задачи. В краткой записи фиксирую величины, числа – данные и искомые, а также некоторые слова, показывающие, о чем говорится в задаче: «было», «положили», «стало» и т.п. Краткую запись задачи выполняю в таблице и без нее.
При табличной форме требуется выделение и название величины. Расположение числовых данных помогает установлению связей между величинами: на одной строке, одно под другим. Искомое число обозначается вопросительным знаком.
С первого класса знакомлю учащихся с простейшим предметным моделированием. В вазе лежало 3 яблока и 2 апельсина. Сколько всего фруктов лежало в вазе?
Выставляю предметные картинки на наборное полотно. После повторного прочтения задачи и разбора условия, учащиеся заменяют картинки кружками (переходим от предмета к графическому моделированию).
- Как можно изобразить эти фрукты в тетради?
- Кружками разного цвета – красного и оранжевого.
В тетради получается графическая модель задачи:

На следующих этапах решения задач (когда учащиеся познакомились с отрезками, сложением и вычитанием отрезков) используем более сложные модели: схематический рисунок и схемы.
| Схематический рисунок: | Схема: |
| 
| 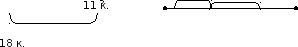 |
Одним из основных приёмов в анализе задачи, на мой взгляд, является моделирование, которое помогает ученику не только понять задачу, но и самому найти рациональный способ её решения.
Так, анализируя задачу: «На уборке урожая работало 12 тракторов. Грузовиков было на 3 больше чем тракторов. Комбайнов работало на 7 меньше, чем грузовиков. Сколько было комбайнов?» [5, с. 112], кратко записываем её в таком виде:
 Тр. – 12 шт.
Тр. – 12 шт.

Гр. - ?, на 3 м. больше
К. - ?, на 7 м. меньше
Такая запись при первичном анализе нерациональна, так как не раскрывает наглядно взаимозависимостей между данными и искомыми, не помогает в выборе действий. Поэтому предлагаю учащимся смоделировать её так:
12 шт.

![]() Тр.
Тр.
на 3 м. больше

 Гр.
Гр.
на 7 м. меньше
 К.
К.
Такая модель даёт младшим школьникам наглядное представление об отношениях между данными и искомыми величинами в задаче.
При самостоятельном решении задач младшие школьники выбирают из предложенных моделей ту, которая им более удобна (Приложение 3).
При решении составных задач рассматриваем с учащимися, как можно использовать графические модели. Условия с пропорциональными величинами обычно кратко записываем в таблицу. Например: В 6 ящиках 30 кг ягод. Сколько ягод в двух таких ящиках? [6, с. 90]
Она предполагает уже хорошее знание учащимися взаимосвязей пропорциональных величин, т. к. сама таблица этих взаимосвязей не показывает.
| Масса ягод в одном ящике | Количество ящиков | Общая масса |
| одинаковая | 6 2 | 30 кг ? кг |
При первичном знакомстве младших школьников с таким видом задач, считаю, что целесообразно смоделировать условие в виде схематического рисунка или чертежа.
30 кг

?
?
При такой модели решение задачи становится более понятным для всех учащихся. Чтобы узнать, сколько килограммов ягод в 2 ящиках, нужно знать, сколько килограммов в одном ящике.
С целью проверки сформированности у учащихся умения самостоятельно анализировать текст задачи и составлять схематическую запись провожу проверочную работу (Приложение 4). Хорошая результативность показывает, что можно приступать к следующему этапу.
III этап. Закрепление у учащихся умения решать задачи с помощью моделирования
Закреплению навыков у учащихся моделирования текстовых задач помогают упражнения творческого характера. К ним относятся моделирование задач повышенной трудности, задач с недостающими и лишними данными, а также упражнения в составлении и преобразовании задач по данным моделям:
1. Работа с незаконченными моделями:
а) дополнение числовых данных и вопроса к предложенной модели;
б) дополнение какой-либо части модели.
2. Исправление специально допущенных ошибок в модели.
3. Составление условия задачи по данной модели.
4. Составление задач по аналогии (Приложение 5).
Моделирование применяю и при обучении детей нахождению различных способов решения задачи, а также при нахождении среди них рационального. Например, даю детям задание: решите задачу разными способами. Выберите из них более удобный. Почему вы выбрали этот способ? Докажите, что он рациональнее других. «Чтобы пошить костюм, надо 3 метра ткани. У портного есть 18 м одной ткани и 27 м другой. Сколько всего костюмов можно пошить из этой ткани?» [7, с. 65] Модель задачи выглядит так:
| Расход на костюм | Количество костюмов | Общая длина |
| 3 м 3 м | ![]() ? ? ? | 18 м 27 м |
По этой модели нами были найдены следующие варианты решения:
| 1 вариант | 2 вариант |
18 + 27 = 45 (м) – всего 45 : 3 = 15 (к.) | 18 : 3 = 6 (к.) – с одной ткани 27 : 3 = 9 (к.) - с другой 6 + 9 = 15 (к.) |
Мы нашли два способа решения. Учащиеся объясняют каждый из них. Все вместе мы выбираем более рациональный способ.
Результативность и эффективность опыта
К концу первого класса учащиеся легко справлялись с решением основных видов задач, предусмотренных программой, выбирали нужную схему из ряда предложенных, сами могли смоделировать задачу. Для проверки усвоения знаний, умений и навыков решения простых текстовых задач младшим школьникам была предложена проверочная работа, которая состояла из 5 задач (Приложение 6). Учащимся необходимо было их решить, воспользовавшись памяткой. Анализ работы показал, что 20 учащихся класса выполнили задания на 100%, трое учащихся – на 80 % (не справились с 1 из задач) и 1 учащийся класса – на 90%. Он допустил ошибку в вычислении при решении первой задачи.
К третьему классу, учащиеся моего класса без особых усилий составляли схемы разных видов задач, что помогало им быстро и правильно находить решения текстовых задач. Учащиеся легко перешли к решению задач на движение, т. К. они могут правильно, ориентируясь на условие задачи, начертить схему.
Анализ контрольных работ (в частности задач) показал, что учащиеся не боятся приступать к решению текстовых задач и практически все решают их верно (Приложение 7).
Процесс моделирования текстовой задачи повышает мыслительную деятельность младших школьников, способствует развитию вариативности мышления, а значит, делает процесс решения задач более интересным. Учащиеся моего класса активно участвуют в школьных олимпиадах, демонстрируя хорошие результаты (Приложение 8), в Республиканском математическом конкурсе «Кенгуру» (Приложение 9).
Заключение
В теории и практике моделирование выступает как особая целенаправленная деятельность, активизирующая учебный процесс. Использование моделирования в процессе обучения математике, на мой взгляд, помогает формировать у учащихся умение решать текстовые задачи, активизирует мыслительную деятельность младших школьников и развивает логическое мышление.
Предлагаю учителям чаще и разнообразнее использовать возможности моделирования при обучении учащихся математике. Об этом, в частности, говорила, выступая на заседании методического объединения учителей начальных классов, а также демонстрировала приёмы работы по моделированию во время проведения урока для учителей города в 2016 г. (Приложение 10).
Следует особое внимание обратить на то, что:
Целенаправленная работа по формированию приемов умственной деятельности младших школьников должна начинаться с первых уроков математики.
Важным этапом работы для достижения наибольшего эффекта является создание модели самими учащимися в процессе решения задачи.
Ученикам с различным уровнем развития требуются различные приёмы работы с задачей. Поэтому на уроках математики необходимо учить детей построению нескольких видов моделей к одной и той же текстовой задаче. Это требуется для того, чтобы дети не оказались в ситуации неуспеха, а чувствовали себя способными решить задачу, выбирая для себя наиболее удобный способ.
Использование графического моделирования учащимися при решении текстовых задач обеспечит более качественный анализ задачи, осознанный поиск её решения, обоснованный выбор арифметических действий и предупредит многие ошибки в решении задач.
В целом полученные результаты дают основание предположить, что опыт
моей работы по моделированию текстовых задач на уроках математики имеет практическую значимость для повышения качества образовательного процесса.
Список литературы
Дрозд, В.Л. Методика начального обучения математике /В.Л. Дрозд и др.; под общей ред. А.А. Столяра и В.Л. Дрозда. – Минск: Выш. Школа, 1988.
Словарь иностранных слов. 16-е изд., испр. – М.: Русский язык, 1988.
Урбан, М. А. Использование учебных моделей при решении простых задач / М. А. Урбан // Пачатковая школа. – 2011. – № 11.
Урбан, М. А. Работа с моделями на уроках математики / М. А. Урбан // Пачатковая школа. – 2010. – № 4.
Чеботаревская, Т.М., Николаева, В.В. Математика: учебное пособие для 2 класса учреждений общего среднего образования с русским языком обучения. В 2 ч. Ч. 1 / Т.М. Чеботаревская, В.В. Николаева. – Минск: Адукацыя і выхаванне, 2012.
Чеботаревская, Т.М., Николаева, В.В. Математика: учебное пособие для 3 класса учреждений общего среднего образования с русским языком обучения. В 2 ч. Ч. 1 / Т.М. Чеботаревская, В.В. Николаева. – Минск: Адукацыя і выхаванне, 2013.
Чеботаревская, Т.М., Николаева, В.В. Математика: учебное пособие для 3 класса учреждений общего среднего образования с русским языком обучения. В 2 ч. Ч. 2 / Т.М. Чеботаревская, В.В. Николаева. – Минск: Адукацыя і выхаванне, 2013.
Приложение 1
Виды заданий, используемых на разных этапах урока
для отработки умения выделять величины и их отношения
1. В магазин привезли 12 кг картофеля и 5 кг моркови. За день продали 7 кг овощей. Сколько килограммов овощей осталось в магазине?
- Назови опорные (основные) слова.
2. Второклассники сделали закладки. Несколько закладок они отдали первоклассникам. Сколько закладок осталось у второклассников?
- Выпишите опорные (основные) слова в столбик;
- Поставьте между опорными словами знаки «+», « - » и обоснуйте свой выбор, почему выбрали тот или иной знак;
- Какое слово в задаче заменяет самое большое число?
- Какое слово в задаче заменяет самое маленькое число?
3. На столе 8 тетрадей в клетку и столько же в линейку. Сколько всего тетрадей на столе?
- Изобразите с помощью квадратов красного и желтого цвета, о чем говорится в задаче.
- Что обозначают квадраты красного цвета?
- Что обозначают квадраты желтого цвета?
4. На магнитной доске выставлены жёлтые треугольники, условно они обозначают лисички, а жёлтые круги – боровики.
- Составьте задачу.
- Покажите те фигуры, число которых требуется узнать в задаче.
5. У Тони 15 карандашей, а у Светы – на 4 карандаша меньше. Сколько карандашей у девочек всего?
-Покажи соответствующую модель к данной задаче (предложено несколько моделей).
6. В вазе лежало 9 груш и 5 яблок. 7 фруктов съели. Сколько фруктов осталось в вазе?
- Подчеркни красным карандашом опорные (основные) слова.
- Запиши кратко задачу.
7. На пошив костюма расходуют по 3 м ткани. Сколько таких костюмов можно сшить из 12 м ткани?
- Условимся изображать 1 м ткани отрезком в 1см.
- Изобразите весь имеющийся материал в виде отрезка АВ.
- Опираясь на чертеж дайте ответ на вопрос задачи.
Приложение 2
Проверочная работа (1 класс)
Цель: определение степени усвоения учащимися умения находить в текстовой задаче отношения и величины, умения самостоятельно дополнять условие задачи числовыми данными, умения составить рисунок к задаче, умения устанавливать связи между данными и искомыми числами и на этой основе выбирать соответствующее арифметическое действие.
Проводится в виде проверочной работы, состоящей из текста задачи, и предложенных четырех заданий к ней.
Инструкция: Внимательно прочитай задачу и задания.
На полке было 11 книг. Когда несколько книг взяли, то на полке осталось □ книг. Сколько книг взяли с полки?
1 задание: Подчеркни красным карандашом опорные (основные) слова.
2 задание: Подбери пропущенное число в условии задачи (вставь его в пустое окошечко). Прочитай полученную задачу.
3 задание: Нарисуй столько кружков, сколько пальто было на вешалке, а затем раскрась столько кружков, сколько пальто осталось на вешалке. Подумай, что обозначают не закрашенные кружки.
4 задание: Запиши решение задачи.
Обработка полученных данных: за каждый правильный ответ ставится 1 балл. Максимальное количество – 4 балла.
Низкий уровень – от 0 до 2 баллов, нуждается в подсказках.
Средний уровень – 3 балла, не уверен, делает ошибки.
Высокий уровень – 4 балла, уверен и самостоятелен.
Приложение 3
Виды заданий, используемых для отработки умения
 самостоятельно анализировать и решать задачи
самостоятельно анализировать и решать задачи

Прочитай текст задачи и доделай любой из вариантов её краткой записи. Запиши решение задачи.
 В автобусе ехало 43 человека. На остановке 16 человек вышли, а 7 человек зашли. Сколько пассажиров стало в автобусе?
В автобусе ехало 43 человека. На остановке 16 человек вышли, а 7 человек зашли. Сколько пассажиров стало в автобусе?



Было - __ п.
Вышли - __ п.
Зашли - __ п.
Стало - __ п.





Прочитай текст задачи. Среди предложенных моделей выбери ту, которая подходит к задаче. Дополни её числовыми данными. Реши задачу.

 На ветке 8 ласточек и 2 воробья. На сколько больше ласточек, чем воробьёв?
На ветке 8 ласточек и 2 воробья. На сколько больше ласточек, чем воробьёв?
![]()
 б) в)
б) в)








Приложение 4
Проверочная работа (2 класс)
Цель: определение у учащихся умения самостоятельно анализировать текст задачи и составлять схематическую запись.
Проводится в виде проверочной работы, состоящей из 4 задач.
Инструкция: Проверь, сколько задач ты сможешь правильно проанализировать (другими словами, составить краткую или схематическую запись) за отведённое время. Записывать решение задачи не надо.
Рыболов поймал 27 рыб. Из них: 9 окуней, 5 щук, а остальные – караси. Сколько карасей поймал рыболов?
9 туристов разместились в палатки, по 3 человека в каждую. Сколько палаток им понадобилось?
В одном вагоне было 37 человек, а во втором – на 10 человек больше. Сколько всего человек было в двух вагонах?
Валя срезала 6 роз и поставила их в две вазы поровну. По сколько роз поставила Валя в каждую вазу?
Обработка полученных данных: за каждый правильный ответ ставится 1 балл. Максимальное количество – 4 балла.
Низкий уровень – от 0 до 2 баллов, нуждается в подсказках.
Средний уровень – 3 балла, не уверен, делает ошибки.
Высокий уровень – 4 балла, уверен и самостоятелен.
Приложение 5
Виды заданий, используемых для закрепления навыков
у учащихся моделирования текстовых задач
Реши задачи при помощи чертежа. Найди задачи-ловушки, исправь их и реши.
В вазе стояли тюльпаны. Когда из них 4 завяли, осталось 6 тюльпанов. Сколько тюльпанов было в вазе первоначально?
У Саши 12 марок. Когда ему подарили ещё несколько марок, то всего их стало 10. Сколько марок подарили Саше?
В бригаде было 6 девочек и 5 мальчиков. Девочки собрали 4 кг клубники, мальчики столько же. Сколько всего детей собрало клубнику?
Продолжи задачу соответственно чертежу. Реши задачу.
В гараже стояло 28 легковых машин, а грузовых…
![]()


28 м.

? на 15 м. больше ?
Исправь ошибки в модели и реши задачу.


 На продажу в ларёк привезли розы. В первый день продали 27 роз, во второй – 20. Сколько роз привезли в ларёк, если осталось продать 9 роз?
На продажу в ларёк привезли розы. В первый день продали 27 роз, во второй – 20. Сколько роз привезли в ларёк, если осталось продать 9 роз?




27 р. 20 р.
? 9 р.
Дополни модель и реши задачу.
В первом ящике 40 кг картошки, во втором – на 6 кг больше, чем в первом, а в третьем ящике на 15 кг меньше, чем во втором. Сколько килограммов картошки во всех трёх ящиках?
![]()


Ι


ΙΙ

ΙΙΙ
Прочитай задачу. Заполни таблицу. Реши задачу. Составь свою задачу про фрукты, аналогичную данной.
В магазин привезли 5 мешков картофеля по 45 кг в каждом и 7 ящиков моркови по 12 кг в каждом. Сколько килограммов овощей привезли в магазин?
| Масса в 1 | Количество | Общая масса |
| __________ __________ | ______ ______ | ![]() ___ __ ___ |
Воспользовавшись таблицей вставь в условие задачи недостающие данные и реши её.
Винни-Пух за месяц съел __ бочонка с мёдом, в каждом их которых было по ___ кг. За второй месяц он съел __ бочонка мёда по ____ кг в каждом. Сколько килограммов мёда съел Винни-Пух за _________________ ?
| Масса в 1 | Количество | Общая масса |
| 60 кг 55 кг | 3 б. 4 б. | ![]() ? ?_ ? |
Приложение 6
Проверочная работа в 1 классе
Цель: определение уровня сформированности умения решать простые текстовые задачи.
Инструкция: реши задачи, воспользуйся памяткой.
Саша купил 8 ручек, а Коля на 6 ручек больше. Сколько ручек купил Коля?
У Оли 4 голубых и столько же красных шаров. Сколько всего шаров у Оли?
Коля и Витя нашли всего 17 грибов, 10 грибов нашёл Коля, а остальные Витя. Сколько грибов нашёл Витя?
На тарелке лежали яблоки. Когда семья съела 4 яблока, то на тарелке их осталось 5. Сколько яблок было на тарелке?
Мама купила 10 ручек. Когда она дала сыну несколько ручек, то у мамы их осталось 6. Сколько ручек мама дала сыну?
Памятка работы над задачей
Прочитай текст задачи.
Подчеркни опорные (основные) слова.
Выдели величины, данные в условии задачи.
Прочитай задачу и построй модель в соответствии с отношением выделенных величин.
Обозначь на модели известные величины.
Неизвестные величины на модели обозначь вопросом.
С опорой на модель найди зависимость между величинами.
Запиши решение задачи.
Запиши ответ.
Сделай проверку.
Анализ результатов
| № задачи | Правильно | Ошибка в вычислении | Ошибка в рассуждении |
-
| 22 | 1 | 1 |
-
| 24 | - | - |
-
| 24 | - | - |
-
| 24 | - | - |
-
| 22 | - | 2 |
Приложение 7
Анализ результатов решения задач при проведении контрольных работ
| № | Ф.И. учащихся | 1 класс | 2 класс | 3 класс | 4 кл. |
| 1 четверть | 2 четверть | 3 четверть | 4 четверть | 1 четверть | 2 четверть | 3 четверть | 4 четверть | 1 четверть |
-
| Акулич Илья | н/б |
|
|
|
| н/б |
|
|
|
|
-
| Астапенко Света |
|
| н/б |
|
|
| н/б |
|
|
|
-
| Бабицкий Егор |
|
|
|
|
|
|
|
|
|
|
-
| Василевская Ксения |
|
|
|
|
|
|
|
|
|
|
-
| Гайдук Матвей |
|
|
|
|
|
|
|
|
|
|
-
| Гришко Анна |
|
|
|
|
|
|
|
|
|
|
-
| Гурков Савелий |
|
| н/б |
|
|
|
|
|
|
|
-
| Дашкевич Полина |
|
|
|
|
|
|
|
|
|
|
-
| Караян Алина |
|
|
|
|
|
|
|
|
|
|
-
| Копач Стефания |
|
|
|
|
|
|
|
|
|
|
-
| Лещенко Анна |
|
| н/б |
|
|
|
|
|
|
|
-
| Лютаревич Лия |
|
|
|
|
|
|
|
|
|
|
-
| Мазынская Мария | н/б |
|
|
|
|
|
|
|
|
|
-
| Максимов Станислав |
|
|
|
| н/б |
| н/б |
| н/б |
|
-
| Матюшонок Полина |
|
|
|
|
|
|
|
|
|
|
-
| Перфилов Михаил |
|
|
|
|
|
|
|
|
|
|
-
| Петрович Владимир |
|
| н/б |
|
|
|
|
|
|
|
-
| Позняк Фёдор |
|
|
|
|
|
|
|
|
|
|
-
| Савельева Анастасия |
|
|
|
|
|
|
|
|
|
|
-
| Сидорович Даниил |
|
|
|
|
|
|
|
|
|
|
-
| Сорокин Александр |
|
| н/б |
|
|
|
|
|
|
|
-
| Чучкевич Алина |
|
|
|
|
|
|
|
|
|
|
-
| Юркевич-Войнич Назар |
|
|
|
|
|
|
|
|
|
|
-
| Яхновец Михаил |
| н/б | н/б |
|
|
|
|
| н/б | н/б |
-
| Филипова Диана | Прибыла в 3 класс |
|
|
| н/б |
|
| Всего писало работу | 22 | 23 | 18 | 24 | 23 | 24 | 23 | 25 | 22 | 24 |
|  Решили верно Решили верно
| 22 | 19 | 14 | 17 | 16 | 17 | 20 | 21 | 16 | 21 |
|  Ошибки в вычислениях Ошибки в вычислениях
| - | 2 | 2 | 3 | 4 | 4 | 2 | 1 | 1 | 1 |
|  Ошибки в рассуждении Ошибки в рассуждении
| - | 2 | 2 | 4 | 3 | 3 | 1 | 3 | 4 | 2 |
|  Не приступили к решению Не приступили к решению
| - | - | - | - | - | - | - | - | 1 | - |
Приложение 8
Участие учащихся класса в школьных олимпиадах по математике
2 класс
| № | Ф.И. учащегося | Балл | % | Место |
-
| Бабицкий Егор | 23 | 74% | 1 место |
-
| Копач Стефания | 15 | 48% |
|
-
| Василевская Ксения | 13 | 42% |
|
-
| Сидорович Даниил | 12 | 39% |
|
3 класс
| № | Ф.И. учащегося | Балл | % | Место |
-
| Бабицкий Егор | 29 | 97% | 1 место |
-
| Савельева Анастасия | 18 | 60% | 3 место |
-
| Сорокин Александр | 18 | 60% | 3 место |
-
| Лещенко Анна | 16 | 53% | 3 место |
-
| Копач Стефания | 8 | 47% |
|
Приложение 9
Участие в Республиканском математическом конкурсе «Кенгуру»
| Учебный год | Класс | Количество участников | Приз 3 | Приз 4 |
| 2013/2014 | 1 класс | 4 | 1 Бабицкий Егор |
|
| 2014/2015 | 2 класс | 8 | 1 Бабицкий Егор | 1 Савельева Анастасия |
| 2015/2016 | 3 класс | 18 | - | 2 Василевская Ксения, Яхновец Михаил |
Приложение 10
Урок математики в 3 классе
Тема: «Вычитание трёхзначных чисел без перехода через разряд»
Раздел: Трёхзначные и четырёхзначные числа
Тип урока: урок изучения нового материала.
Цель урока: знакомство с алгоритмом вычитания трёхзначных чисел без перехода через разряд, аналогичному приёму вычитания двузначных чисел
Задачи урока:
- «открыть» приём вычитания трёхзначных чисел без перехода через разряд на основании умения вычитать двузначные числа;
- способствовать формированию навыков анализа и решения составных задач;
- развивать вычислительные навыки;
- содействовать формированию умения планировать, контролировать и оценивать учебные действия;
- способствовать воспитанию трудолюбия, самостоятельности, аккуратности при выполнении заданий, сопереживания и стремления к результативности.
Оборудование: учебник, веера цветов, сигнальные карточки для рефлексии, мультимедийная презентация, карточки для самостоятельной работы по уровням, карточки для индивидуальной работы
Ход урока
1. Организация начала урока (слайд 1)
2. Устный счёт, чистописание Работа с рядом чисел (слайд 2):
Работа с веерами чисел: решение задач.
Лодка проплыла 21 км за 3 часа. С какой скорость плыла лодка? Как нашли? Как находим скорость? (Чтобы найти скорость, надо расстояние разделить на время.) (слайд 3)
Затем лодка развернулась и проплыла в обратном направлении 28 км с той же скорость. Сколько времени плыла лодка в обратном направлении? Как нашли? Как находим время? (Чтобы найти время, необходимо расстояние разделить на скорость.)
А сколько времени лодка была в пути всего? Как нашли?
На озере плавало 8 лодок. 2 из них причалили к берегу. Сколько лодок осталось на озере? Почему? (слайд 4)
Молодцы! Справились со всеми заданиями.
3. Физминутка для глаз (слайды 6 - 9)
4. Актуализация знаний
На экране примеры (слайд 10):
74 + 24 85 – 42
315 + 423 465 – 234
Нужно примеры записать в «столбик» и решить. Решаем первый столбик.
5. Сообщение темы урока, целей
Посмотрите на второй столбик. Что общего? Решаем первый пример на вычитание (двузначные числа). При проверке вспоминаем алгоритм вычитания двузначных чисел без перехода через разряд. Какой пример остался? Решали ли мы раньше такие примеры? Как вы думаете, над чем мы будем работать сегодня на уроке? (слайд 11). Какую цель вы поставите перед собой?
Каким образом мы можем достичь поставленной цели?
Изучение нового материала
Составление алгоритма вычитания трёхзначных чисел без перехода через разряд. (слайд 12)
Закрепление изученного материала
Работа с учебником (слайд 13). Выполнение вычислений в столбик № 1 на стр. 62. Самопроверка.
Физминутка подвижная
Работа над задачей (слайд 14)
![]()
![]() Найдите № 4 на стр. 63. Составление коллективно модели:
Найдите № 4 на стр. 63. Составление коллективно модели:
Медведи Кот S - 24 км t - ? ч Vм.= Vк.


S - 32 км t - 4 ч
Кто ехал на велосипедах? Кто проехал больше? Какое расстояние проехали медведи? Где показать? Какое расстояние проехал кот? Как показать? Какие данные ещё известны? Что требуется найти в задаче? Как находим время? (Чтобы найти время, необходимо расстояние разделить на скорость.) Расстояние известно? А скорость? Можем ли сразу найти время? Что нам известно про скорость? А скорость медведей известна? А можем найти? Как нужно находить скорость? (Чтобы найти скорость, надо расстояние разделить на время.) Все данные известны? Так что будем находить вначале задачи? Как? Что затем? Как?

 32 : 4 Самостоятельное решение задачи учащимися.
32 : 4 Самостоятельное решение задачи учащимися.


 Двое учащихся у доски. Проверка (сравнение).
Двое учащихся у доски. Проверка (сравнение).
 24 : ?
24 : ?



?
Для более сильных учащихся задача с изменением вопроса: На сколько меньше времени находился в пути кот, чем медведи? (индивидуальная проверка) Оцените решение задачи: правильность.
Самостоятельная работа
Индивидуальная работа с карточками по уровням.
Проверка правильности выполнения заданий (слайд 15).
Домашнее задание
Стр. 63, № 8 (воспользовавшись алгоритмами сложения и вычитания трёхзначных чисел, решите примеры в столбик) (слайд 16)
Итоги. Рефлексия
- Над какой темой сегодня работали? (слайд 17)
- Каким алгоритмом пользовались?
- Какие цели ставили?
- Достигли ли своей цели? Почему?
- Что получилось?
- Над чем стоит еще поработать?
- Что вы не знали, а сейчас знаете?
- Подумайте, какое настроение у вас на конец урока. Возьмите солнышко, если хорошее, или тучку, если нет. Необходимо поставить их у тех слов, которые больше всего подходят вам.
Конечно, было все понятно.
Лишь кое-что чуть-чуть неясно.
Еще придется потрудиться.
Да, трудно все-таки учиться!
- Оценка работы учащихся на уроке.








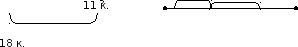
 Тр. – 12 шт.
Тр. – 12 шт.


 Гр.
Гр.  К.
К.
 самостоятельно анализировать и решать задачи
самостоятельно анализировать и решать задачи
 В автобусе ехало 43 человека. На остановке 16 человек вышли, а 7 человек зашли. Сколько пассажиров стало в автобусе?
В автобусе ехало 43 человека. На остановке 16 человек вышли, а 7 человек зашли. Сколько пассажиров стало в автобусе?








 На ветке 8 ласточек и 2 воробья. На сколько больше ласточек, чем воробьёв?
На ветке 8 ласточек и 2 воробья. На сколько больше ласточек, чем воробьёв?









