РЕШУ ОГЭ — математика
Вариант № 65257793
1. Тип 1 № 400935 
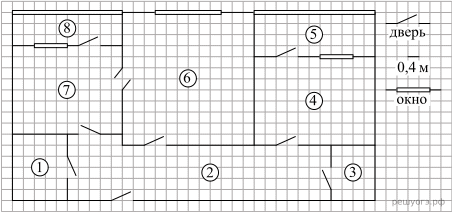
На рисунке изображен план двухкомнатной квартиры в многоэтажном жилом доме. Сторона одной клетки на плане соответствует 0,4 м, а условные обозначения двери и окна приведены в правой части рисунка.
Вход в квартиру находится в коридоре. Слева от входа в квартиру находится санузел, а в противоположном конце коридора — дверь в кладовую. Рядом с кладовой находится спальня, из которой можно пройти на одну из застекленных лоджий. Самое большое по площади помещение — гостиная, откуда можно попасть в коридор и на кухню. Из кухни также можно попасть на застекленную лоджию.
Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк перенесите последовательность четырех цифр без пробелов, запятых и других дополнительных символов.
| Объекты | коридор | кладовая | спальня | гостиная |
| Цифры | | | | |
2. Тип 2 № 409278 
Плитка для пола размером 40 см на 40 см продается в упаковках по 12 штук. Сколько упаковок плитки понадобится, чтобы выложить пол санузла?
3. Тип 3 № 409292 
Найдите площадь санузла. Ответ дайте в квадратных метрах.
4. Тип 4 № 409300 
На сколько процентов площадь коридора больше площади кладовой?
5. Тип 5 № 409308 
В квартире планируется установить стиральную машину. Характеристики стиральных машин, условия подключения и доставки приведены в таблице. Планируется купить стиральную машину с вертикальной загрузкой, не превосходящую 85 см по высоте.
| Модель | Вместимость барабана (кг) | Тип загрузки | Стоимость (руб.) | Стоимость подключения (руб.) | Стоимость доставки (% от стоимости машины) | Габариты (высота × ширина × глубина, см) |
| А | 7 | верт. | 28 000 | 1700 | бесплатно | 85 × 60 × 45 |
| Б | 5 | фронт. | 24 000 | 4500 | 10 | 85 × 60 × 40 |
| В | 5 | фронт. | 25 000 | 5000 | 10 | 85 × 60 × 40 |
| Г | 6,5 | фронт. | 24 000 | 4500 | 10 | 85 × 60 × 44 |
| Д | 6 | фронт. | 28 000 | 1700 | бесплатно | 85 × 60 × 45 |
| Е | 6 | верт. | 27 600 | 2300 | бесплатно | 89 × 60 × 40 |
| Ж | 6 | верт. | 27 585 | 1900 | 10 | 89 × 60 × 40 |
| З | 6 | фронт. | 20 000 | 6300 | 15 | 85 × 60 × 42 |
| И | 5 | фронт. | 27 000 | 1800 | бесплатно | 85 × 60 × 40 |
| К | 5 | верт. | 27 000 | 1800 | бесплатно | 85 × 60 × 40 |
Сколько рублей будет стоить наиболее дешевый подходящий вариант вместе с подключением и доставкой?
6. Тип 6 № 203747 
Запишите десятичную дробь, равную сумме 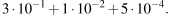
7. Тип 7 № 352483 
Между какими числами заключено число 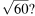
В ответе укажите номер правильного варианта.
1) 20 и 22
2) 7 и 8
3) 59 и 61
4) 3 и 4
8. Тип 8 № 400942 
Найдите значение выражения 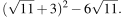
9. Тип 9 № 137381 
Решите уравнение 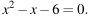
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
10. Тип 10 № 340463 
На экзамене по геометрии школьнику достается одна задача из сборника. Вероятность того, что эта задача по теме «Углы», равна 0,1. Вероятность того, что это окажется задача по теме «Параллелограмм», равна 0,6. В сборнике нет задач, которые одновременно относятся к этим двум темам. Найдите вероятность того, что на экзамене школьнику достанется задача по одной из этих двух тем.
11. Тип 11 № 339073 
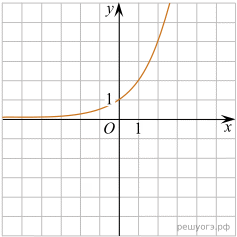
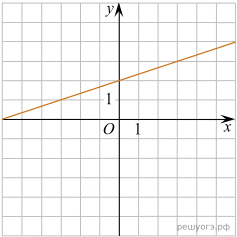
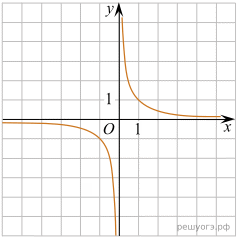
Установите соответствие между функциями и их графиками.
Функции
Графики
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
12. Тип 12 № 316355 
Полную механическую энергию тела (в джоулях) можно вычислить по формуле 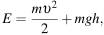 где m — масса тела (в килограммах), υ — его скорость (в м/с), h — высота положения центра масс тела над произвольно выбранным нулевым уровнем (в метрах), а g — ускорение свободного падения (в м/с2). Пользуясь этой формулой, найдите h (в метрах), если
где m — масса тела (в килограммах), υ — его скорость (в м/с), h — высота положения центра масс тела над произвольно выбранным нулевым уровнем (в метрах), а g — ускорение свободного падения (в м/с2). Пользуясь этой формулой, найдите h (в метрах), если 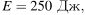
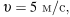
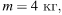 а
а 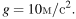
13. Тип 13 № 311310 
Решите неравенство 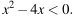
В ответе укажите номер правильного варианта.
1) 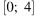
2) 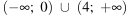
3) 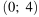
4) 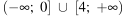
14. Тип 14 № 412224 
У Тани есть теннисный мячик. Она со всей силы бросила его об асфальт. После первого отскока мячик подлетел на высоту 360 см, а после каждого следующего отскока от асфальта подлетал на высоту в три раза меньше предыдущей. После какого по счету отскока высота, на которую подлетит мячик, станет меньше 15см?
15. Тип 15 № 132781 
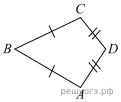 В выпуклом четырехугольнике ABCD
В выпуклом четырехугольнике ABCD 
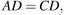
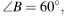
 Найдите угол A. Ответ дайте в градусах.
Найдите угол A. Ответ дайте в градусах.
16. Тип 16 № 333117 
 На окружности с центром O отмечены точки A и B так, что
На окружности с центром O отмечены точки A и B так, что 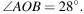 Длина меньшей дуги AB равна 63. Найдите длину большей дуги.
Длина меньшей дуги AB равна 63. Найдите длину большей дуги.
17. Тип 17 № 169881 
Основания трапеции равны 18 и 12, одна из боковых сторон равна 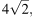 а угол между ней и одним из оснований равен 135°. Найдите площадь трапеции.
а угол между ней и одним из оснований равен 135°. Найдите площадь трапеции.
18. Тип 18 № 311366 
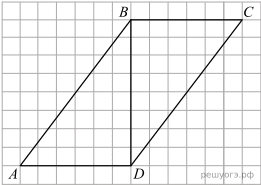 На рисунке с размером клетки 1×1 изображен параллелограмм ABCD. Используя рисунок, найдите
На рисунке с размером клетки 1×1 изображен параллелограмм ABCD. Используя рисунок, найдите 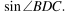
19. Тип 19 № 341410 
Какое из следующих утверждений верно?
1) Точка касания двух окружностей равноудалена от центров этих окружностей.
2) В параллелограмме есть два равных угла.
3) Площадь прямоугольного треугольника равна произведению длин его катетов.
Если утверждений несколько, запишите их номера в порядке возрастания.
20. Тип 20 № 338943 
Решите неравенство 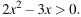
21. Тип 21 № 311558 
Расстояние между городами А и В равно 375 км. Город С находится между городами А и В. Из города А в город В выехал автомобиль, а через 1 час 30 минут следом за ним со скоростью 75 км/ч выехал мотоциклист, догнал автомобиль в городе С и повернул обратно. Когда он вернулся в А, автомобиль прибыл в В. Найдите расстояние от А до С.
22. Тип 22 № 314398 
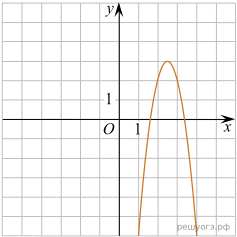
Парабола проходит через точки K(0; –5), L(3; 10), M( –3; –2). Найдите координаты ее вершины.
23. Тип 23 № 339432 
Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 30° и 120°, а CD = 25.
24. Тип 24 № 311606 
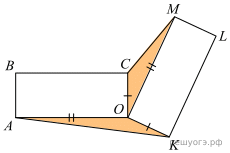 Два равных прямоугольника имеют общую вершину O (см. рис.). Докажите, что площади треугольников AOK и COM равны.
Два равных прямоугольника имеют общую вершину O (см. рис.). Докажите, что площади треугольников AOK и COM равны.
25. Тип 25 № 311562 
Окружность радиуса 4 касается внешним образом второй окружности в точке 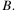 Общая касательная к этим окружностям, проходящая через точку
Общая касательная к этим окружностям, проходящая через точку 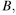 пересекается с некоторой другой их общей касательной в точке A. Найдите радиус второй окружности, если
пересекается с некоторой другой их общей касательной в точке A. Найдите радиус второй окружности, если 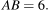









 В выпуклом четырехугольнике ABCD
В выпуклом четырехугольнике ABCD  На окружности с центром O отмечены точки A и B так, что
На окружности с центром O отмечены точки A и B так, что  На рисунке с размером клетки 1×1 изображен параллелограмм ABCD. Используя рисунок, найдите
На рисунке с размером клетки 1×1 изображен параллелограмм ABCD. Используя рисунок, найдите  Два равных прямоугольника имеют общую вершину O (см. рис.). Докажите, что площади треугольников AOK и COM равны.
Два равных прямоугольника имеют общую вершину O (см. рис.). Докажите, что площади треугольников AOK и COM равны.




















