Опорные конспекты по математике

Действительные числа

N :

1;2;3;4;5;6;…

Z

0

-1; -2; -3; -4; …

Q

R

N – множество натуральных чисел Z – множество целых чисел Q – множество рациональных чисел

R – множество действительных чисел

~

~

~

~

~

~

~

~

~

~

~

~

~

~

~

~

~

~

В

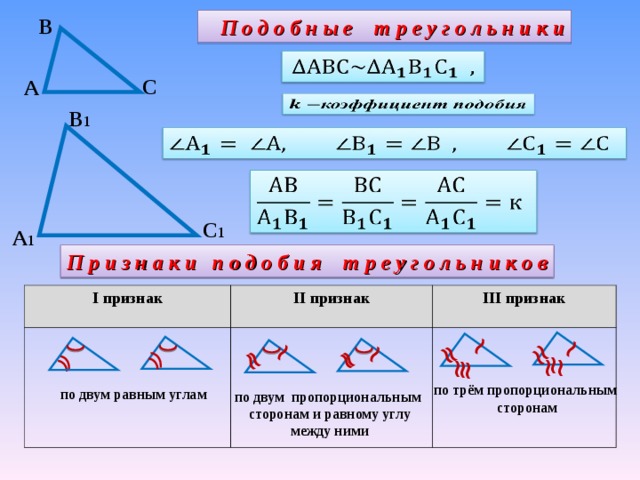
П о д о б н ы е т р е у г о л ь н и к и

С

А

В 1

С 1

А 1

П р и з н а к и п о д о б и я т р е у г о л ь н и к о в

І признак

І І признак

І ІІ признак

по трём пропорциональным

сторонам

по двум равным углам

по двум пропорциональным

сторонам и равному углу

между ними

Некоторые свойства прямоугольных треугольников.

• Сумма острых углов прямоугольного треугольника равна 90 ᵒ .
• Катет прямоугольного треугольника, лежащий против угла в 30 ᵒ , равен

половине гипотенузы.

• Если катет прямоугольного треугольника лежит против угла в 30 ᵒ , то он

равен половине гипотенузы.

Теорема Пифагора. Квадрат гипотенузы прямоугольного треугольника

равен сумме квадратов его катетов.

Пропорциональные отрезки в прямоугольном треугольнике.

1. Высота прямоугольного треугольника, проведённая из вершины прямого

угла, есть среднее пропорциональное для отрезков гипотенузы, на которые

делится гипотенуза этой высотой.

2. Каждый катет прямоугольного треугольника есть среднее

пропорциональное для гипотенузы и отрезка гипотенузы, заключённого

между катетом и высотой, проведённой из вершины прямого угла.

Определение. Два треугольника называются подобными , если углы

треугольников соответственно равны, а стороны одного

треугольника пропорциональны сходственным сторонам

другого. Причём, коэффициент подобия равен отношению

сходственных сторон.

Признаки подобия треугольников.

1. Если два угла одного треугольника равны двум углам другого треугольника,

то треугольники подобны .

2. Если две стороны одного треугольника пропорциональны двум сторонам

другого треугольника, а углы между этими сторонами равны, то

треугольники подобны.

3. Если три стороны одного треугольника пропорциональны трём сторонам

другого треугольника, то треугольники подобны.

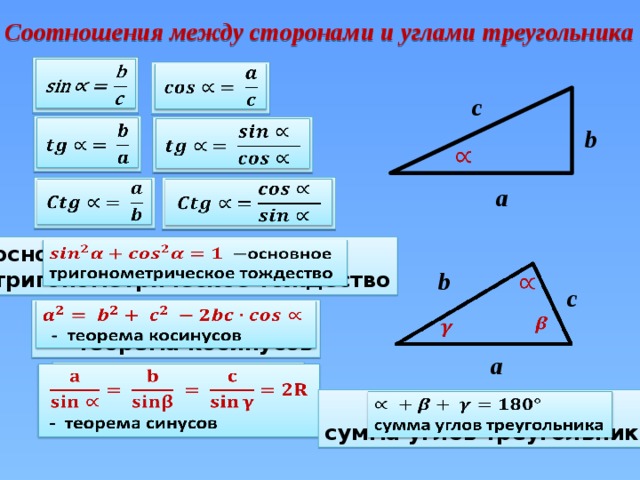
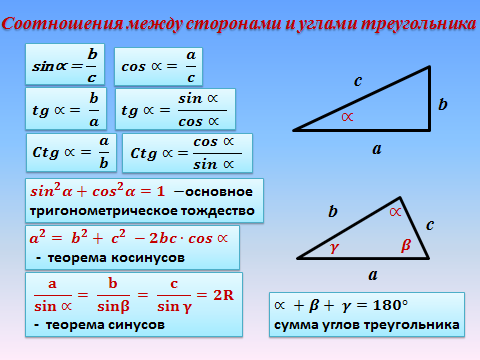
Соотношения между сторонами и углами треугольника

c

b

а

основное

тригонометрическое тождество

b

c

- теорема косинусов

а

- теорема синусов

сумма углов треугольника

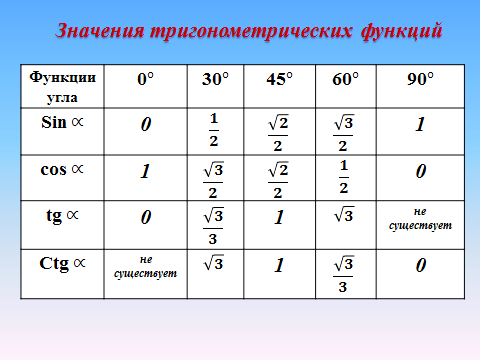
Значения тригонометрических функций

Функции угла

Функции угла

0

Sin

0

30

0

cos

1

1

tg

45

60

0

0

Ctg

90

не

не

1

1

1

1

существует

существует

0

0

1

1

не

не

существует

существует

0

0

Определение. Синусом острого угла прямоугольного треугольника

называется отношение противолежащего катета к гипотенузе.

Определение. Косинусом острого угла прямоугольного треугольника

называется отношение прилежащего катета к гипотенузе

Определение. Тангенсом острого угла прямоугольного треугольника

называется отношение противолежащего катета к прилежащему

Определение. Котангенсом острого угла прямоугольного треугольника

называется отношение прилежащего катета к противолежащему

Теорема косинусов. Квадрат стороны треугольника равен сумме квадратов

двух других его сторон минус удвоенное произведение

этих сторон на косинус угла между ними.

Теорема синусов . Отношения сторон треугольника к синусам противолежащих

углов равны и равны удвоенному радиусу описанной около

треугольника окружности.

Теорема о сумме углов треугольника. Сумма углов треугольника равна 180ᵒ.

b

b

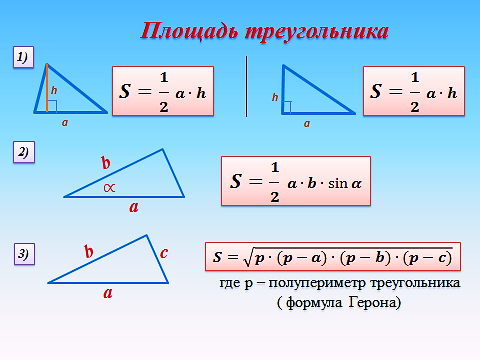
Площадь треугольника

1)

h

h

a

a

2)

а

c

3)

где р – полупериметр треугольника

( формула Герона)

а

1 . Площадь треугольника равна половине произведения основания на высоту.

2 . Площадь прямоугольного треугольника равна половине произведения

его катетов.

3. Если высоты двух треугольников равны, то их площади относятся как

основания.

4. Если два треугольника имеют по одному равному углу, то их площади

относятся как произведения сторон, заключающих равные углы.

5 . Отношение площадей двух подобных треугольников равно квадрату

коэффициента подобия.

6 . Площадь треугольника равна половине произведения двух сторон на синус

угла между ними.

• Формула Герона .

где р – полупериметр треугольника.

,

Скалярное произведение векторов

)

Теорема. Если , , то

Следствия.

,

Если , , то cos

• Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними.

• Теорема . Скалярное произведение векторов и

выражается формулой

• Следствия. 1. Ненулевые векторы и

перпендикулярны тогда и только тогда, когда их скалярное

произведение равно нулю.

2. Косинус угла между ненулевыми векторами

и выражается формулой

cos