Основные формулы школьного курса астрономии 1. Теоретическая разрешающая способность телескопа:
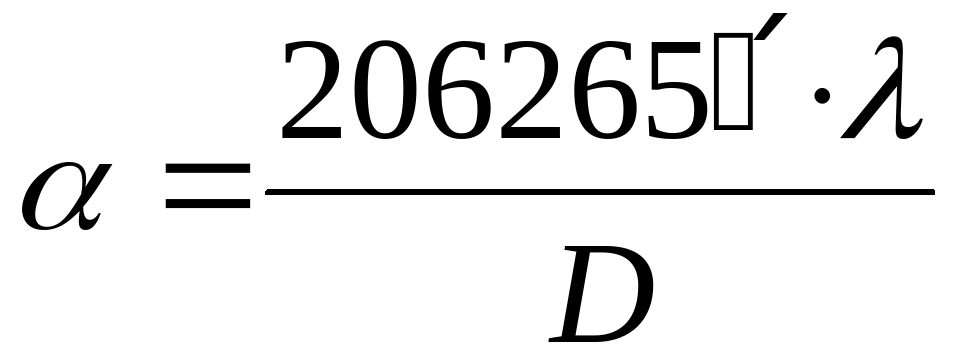 , где λ – средняя длина световой волны (5,5·10-7 м), D – диаметр объектива телескопа, или
, где λ – средняя длина световой волны (5,5·10-7 м), D – диаметр объектива телескопа, или 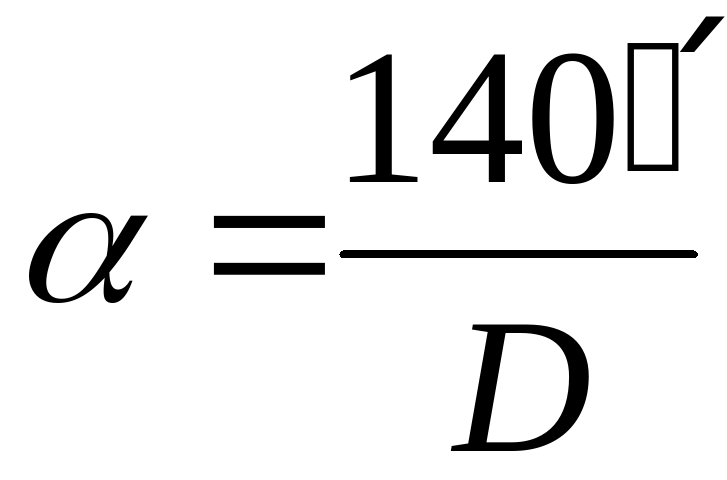 , где D – диаметр объектива телескопа в миллиметрах.
, где D – диаметр объектива телескопа в миллиметрах.
2. Увеличение телескопа:
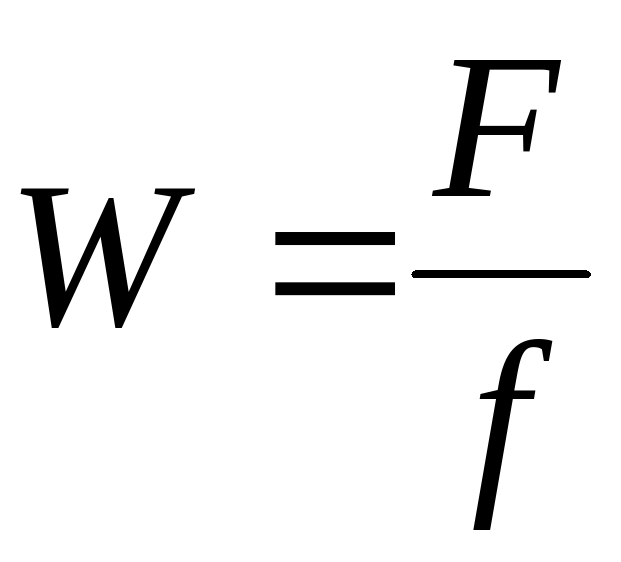 , где F – фокусное расстояние объектива, f – фокусное расстояние окуляра.
, где F – фокусное расстояние объектива, f – фокусное расстояние окуляра.
3. Высота светил в кульминации:
высота светил в верхней кульминации, кульминирующих к югу от зенита ( ):
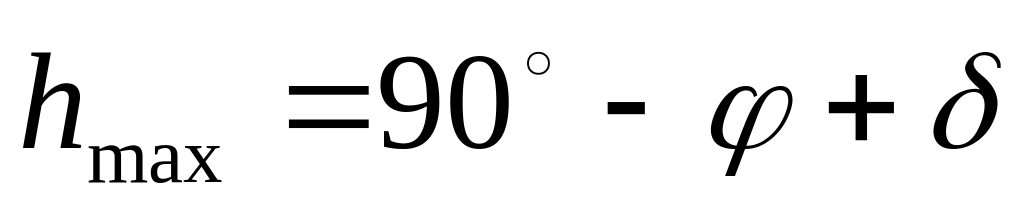 , где – широта места наблюдения, – склонение светила;
, где – широта места наблюдения, – склонение светила;
высота светил в верхней кульминации, кульминирующих к северу от зенита ( ):
 , где – широта места наблюдения, – склонение светила;
, где – широта места наблюдения, – склонение светила;
высота светил в нижней кульминации:
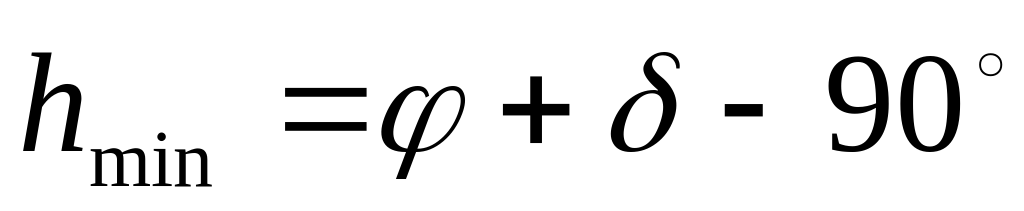 , где – широта места наблюдения, – склонение светила.
, где – широта места наблюдения, – склонение светила.
4. Астрономическая рефракция:
приближенная формула для вычисления угла рефракции, выраженного в секундах дуги (при температуре +10°C и атмосферном давлении 760 мм. рт. ст.):
 , где z – зенитное расстояние светила (для z
, где z – зенитное расстояние светила (для z
5. Время:
звездное время:
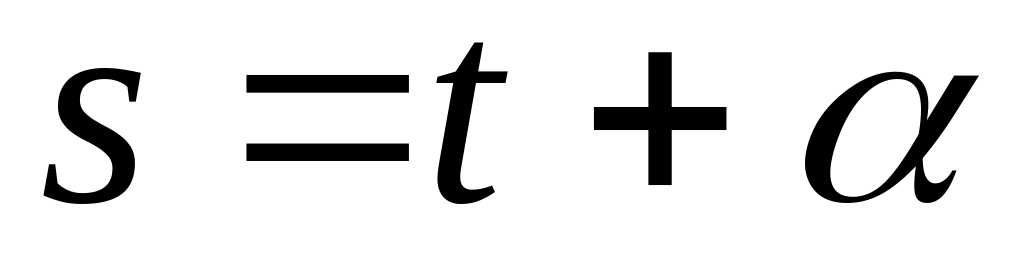 , где – прямое восхождение какого-либо светила, t – его часовой угол;
, где – прямое восхождение какого-либо светила, t – его часовой угол;
среднее солнечное время (местное среднее время):
Tm=T+, где T – истинное солнечное время, – уравнение времени;
всемирное время:
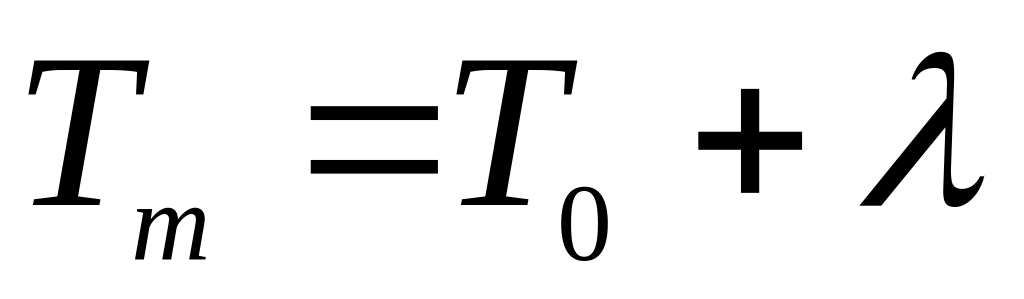 , где – долгота пункта с местным средним временем Tm, выраженная в часовой мере, T0 – всемирное время в этот момент;
, где – долгота пункта с местным средним временем Tm, выраженная в часовой мере, T0 – всемирное время в этот момент;
поясное время:
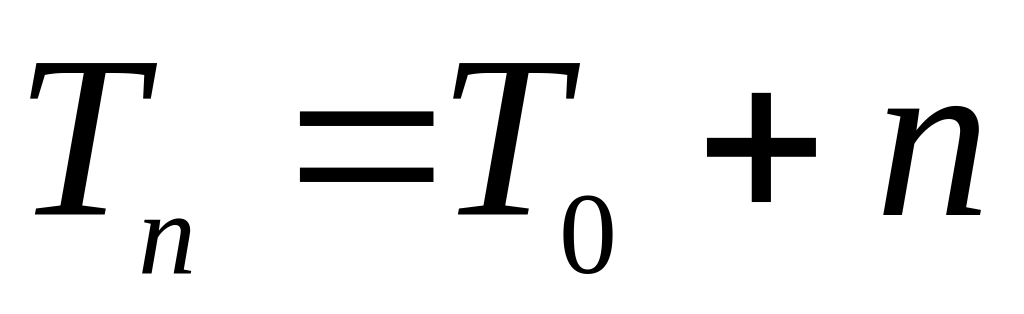 , где T0 – всемирное время; n – номер часового пояса (для Гринвича n=0, для Москвы n=2, для Красноярска n=6);
, где T0 – всемирное время; n – номер часового пояса (для Гринвича n=0, для Москвы n=2, для Красноярска n=6);
декретное время:
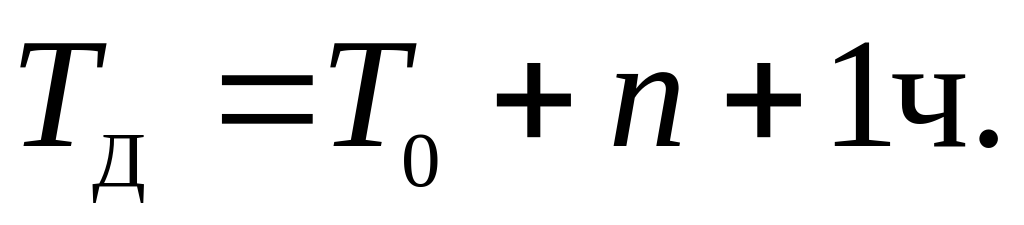 или
или 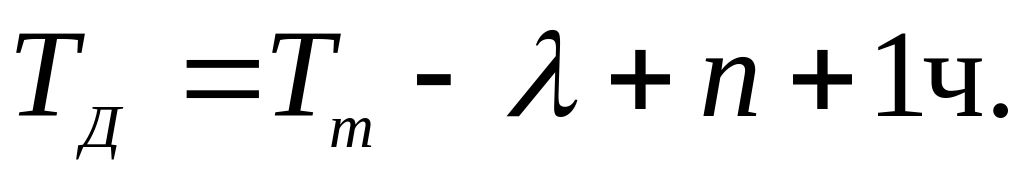
6. Формулы, связывающие сидерический (звездный) период обращения планеты T с синодическим периодом ее обращения S:
для верхних планет:
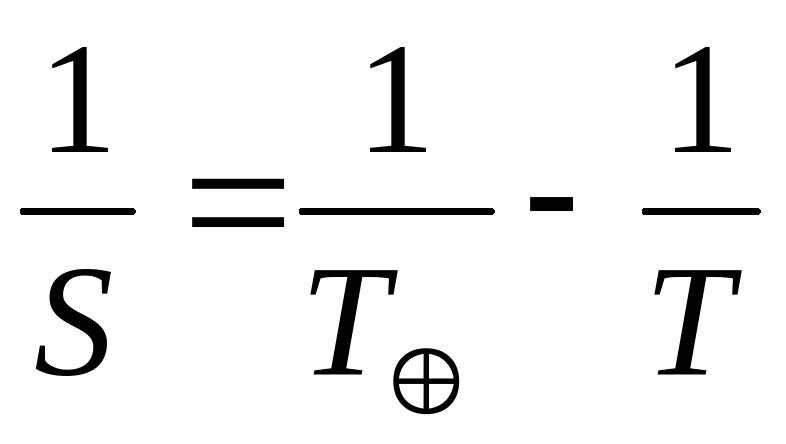 ;
;
для нижних планет:
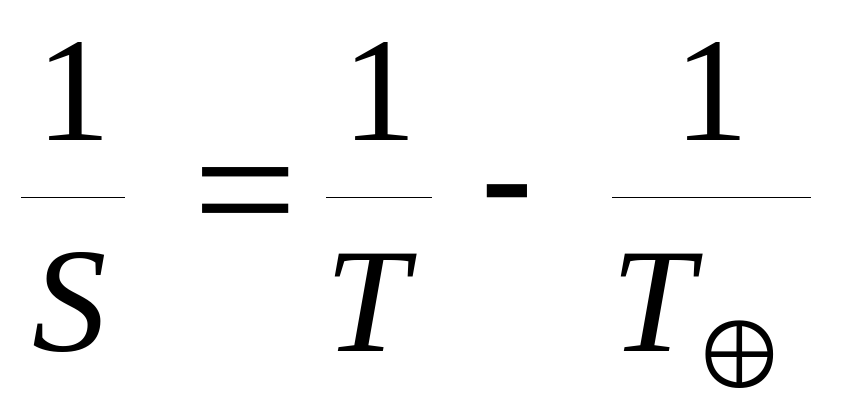 , где T – звездный период обращения Земли вокруг Солнца.
, где T – звездный период обращения Земли вокруг Солнца.
7. Третий закон Кеплера:
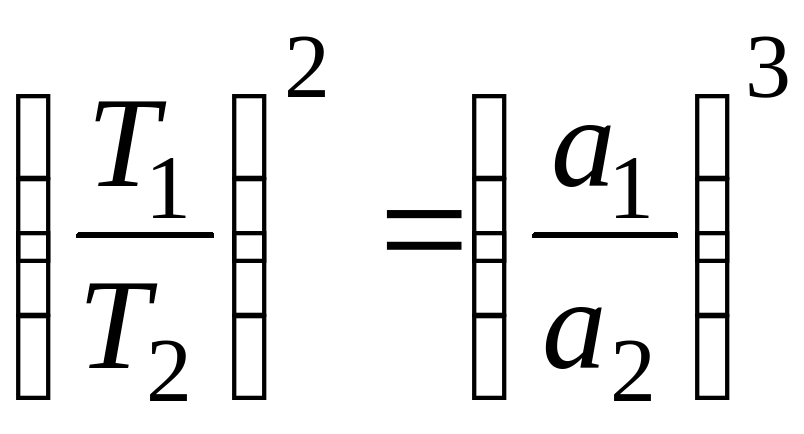 , где Т1 и Т2 – периоды обращения планет, a1 и a2 – большие полуоси их орбиты.
, где Т1 и Т2 – периоды обращения планет, a1 и a2 – большие полуоси их орбиты.
8. Закон всемирного тяготения:
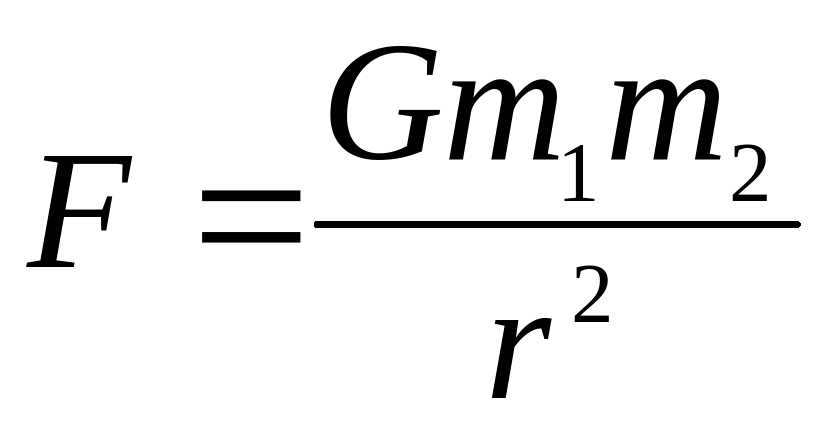 , где m1 и m2 – массы притягивающихся материальных точек, r – расстояние между ними, G – гравитационная постоянная.
, где m1 и m2 – массы притягивающихся материальных точек, r – расстояние между ними, G – гравитационная постоянная.
9. Третий обобщенный закон Кеплера:
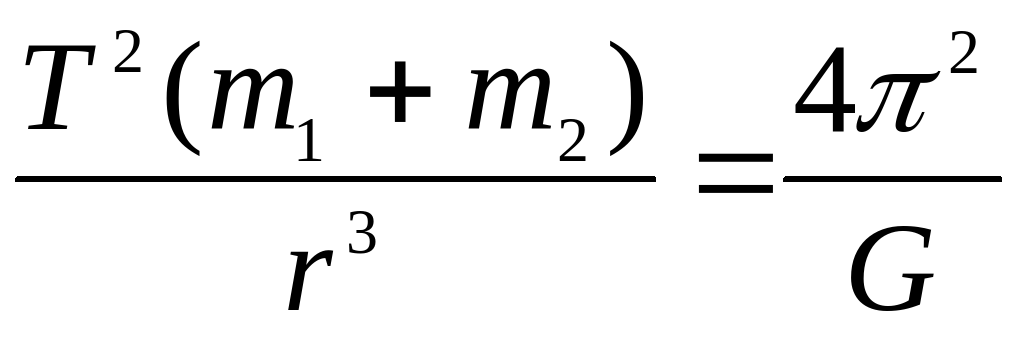 , где m1 и m2 – массы двух взаимно притягивающихся тел, r – расстояние между их центрами, Т – период обращения этих тел вокруг общего центра масс, G – гравитационная постоянная;
, где m1 и m2 – массы двух взаимно притягивающихся тел, r – расстояние между их центрами, Т – период обращения этих тел вокруг общего центра масс, G – гравитационная постоянная;
для системы Солнце и две планеты:
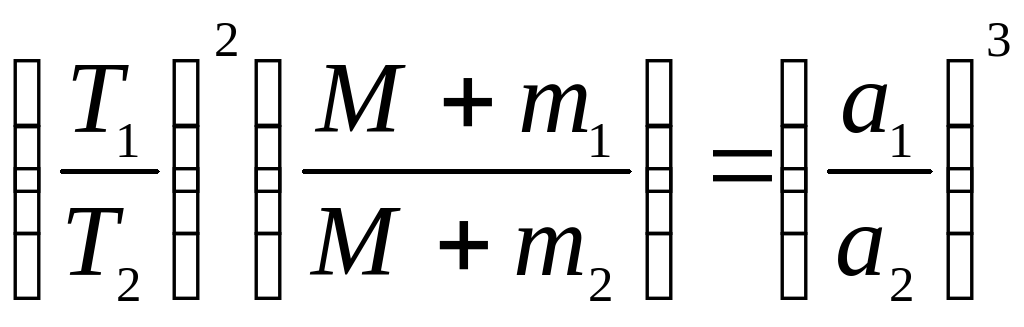 , где Т1 и Т2 – сидерические (звездные) периоды обращения планет, М – масса Солнца, m1 и m2 – массы планет, a1 и a2 –большие полуоси орбит планет;
, где Т1 и Т2 – сидерические (звездные) периоды обращения планет, М – масса Солнца, m1 и m2 – массы планет, a1 и a2 –большие полуоси орбит планет;
для систем Солнце и планета, планета и спутник:
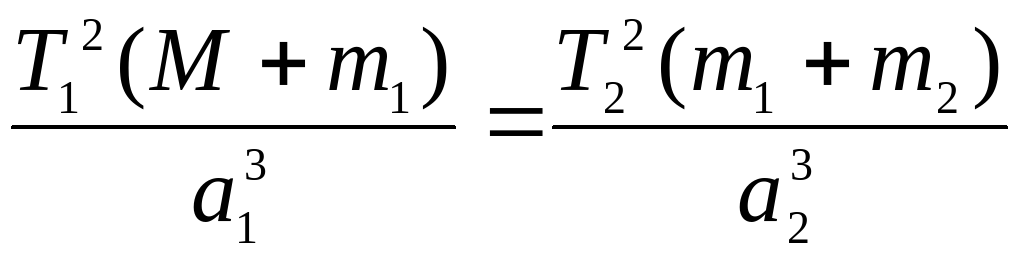 , где M – масса Солнца; m1 – масса планеты; m2 – масса спутника планеты; Т1 и a1 – период обращения планеты вокруг Солнца и большая полуось ее орбиты; Т2 и a2 – период обращения спутника вокруг планеты и большая полуось его орбиты;
, где M – масса Солнца; m1 – масса планеты; m2 – масса спутника планеты; Т1 и a1 – период обращения планеты вокруг Солнца и большая полуось ее орбиты; Т2 и a2 – период обращения спутника вокруг планеты и большая полуось его орбиты;
при M m1, а m1 m2,
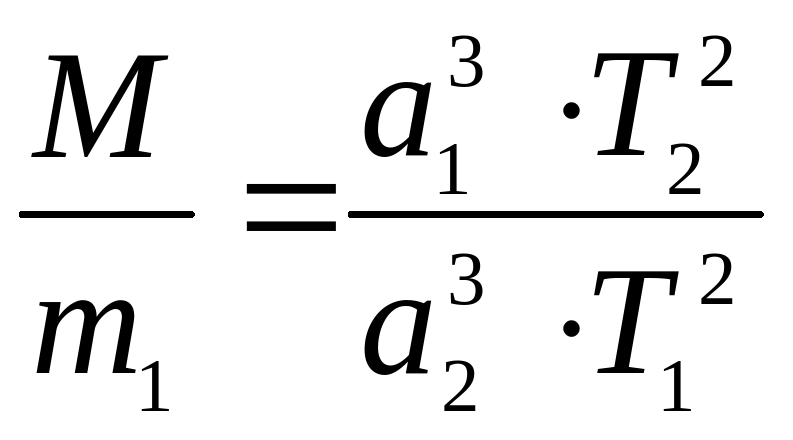 .
.
10. Линейная скорость движения тела по параболической орбите (параболическая скорость):
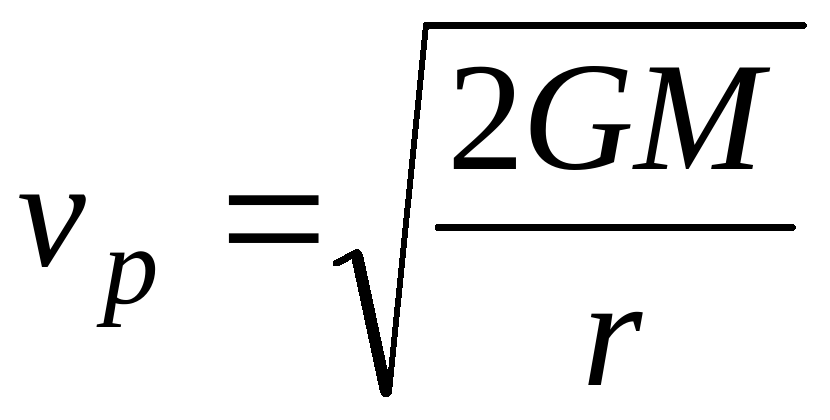 , где G – гравитационная постоянная, M – масса центрального тела, r – радиус-вектор избранной точки параболической орбиты.
, где G – гравитационная постоянная, M – масса центрального тела, r – радиус-вектор избранной точки параболической орбиты.
11. Линейная скорость движения тела по эллиптической орбите в избранной точке:
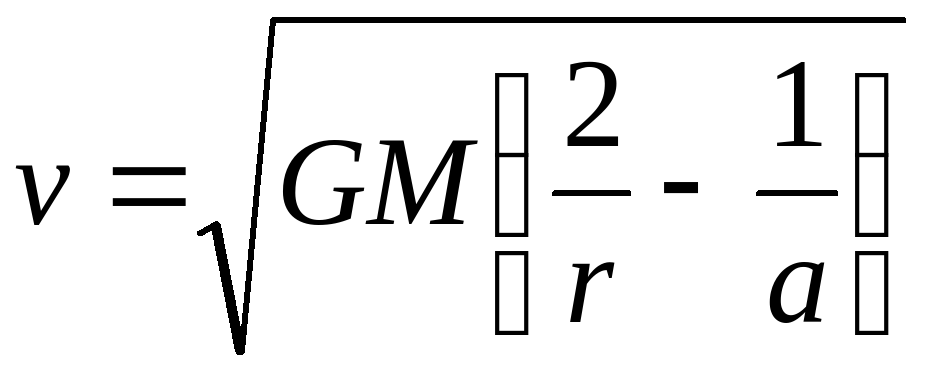 , где G – гравитационная постоянная, M – масса центрального тела, r – радиус-вектор избранной точки эллиптической орбиты, a – большая полуось эллиптической орбиты.
, где G – гравитационная постоянная, M – масса центрального тела, r – радиус-вектор избранной точки эллиптической орбиты, a – большая полуось эллиптической орбиты.
12. Линейная скорость движения тела по круговой орбите (круговая скорость):
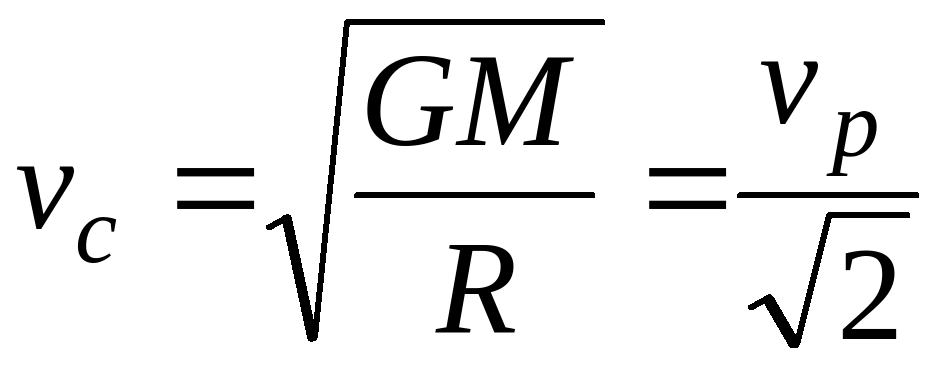 , где G – гравитационная постоянная, M – масса центрального тела, R – радиус орбиты, vp – параболическая скорость.
, где G – гравитационная постоянная, M – масса центрального тела, R – радиус орбиты, vp – параболическая скорость.
13. Эксцентриситет эллиптической орбиты, характеризующий степень отклонение эллипса от окружности:
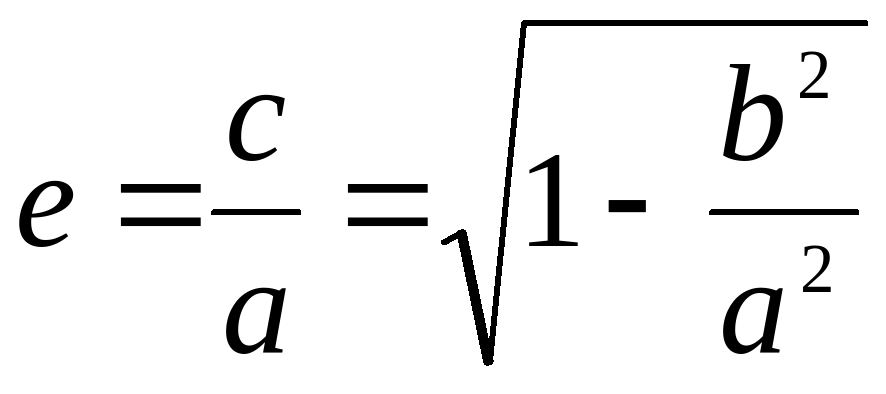 , где c – расстояние от фокуса до центра орбиты, a – большая полуось орбиты, b – малая полуось орбиты.
, где c – расстояние от фокуса до центра орбиты, a – большая полуось орбиты, b – малая полуось орбиты.
14. Связь расстояний перицентра и апоцентра с большой полуосью и эксцентриситетом эллиптической орбиты:
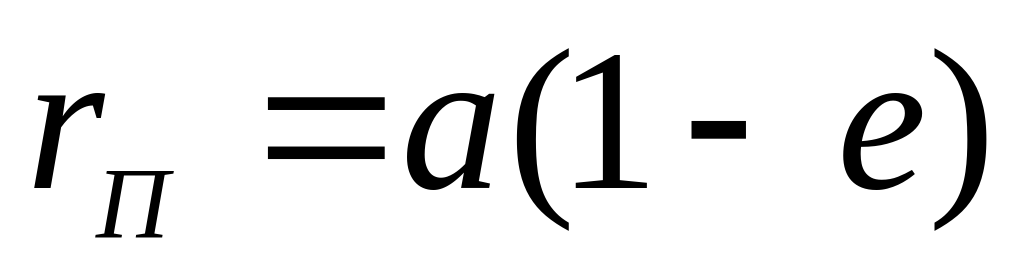 , , , где rП – расстояния от фокуса, в котором находится центральное небесное тело, до перицентра, rА – расстояния от фокуса, в котором находится центральное небесное тело, до апоцентра, a – большая полуось орбиты, e – эксцентриситет орбиты.
, , , где rП – расстояния от фокуса, в котором находится центральное небесное тело, до перицентра, rА – расстояния от фокуса, в котором находится центральное небесное тело, до апоцентра, a – большая полуось орбиты, e – эксцентриситет орбиты.
15. Расстояние до светила (в пределах Солнечной системы):
, где R – экваториальный радиус Земли, ρ0– горизонтальный параллакс светила, выраженный в секундах дуги,
или , где D1 и D2 – расстояния до светил, ρ1 и ρ2 – их горизонтальные параллаксы.
16. Радиус светила:
, где ρ – угол, под которым с Земли виден радиус диска светила (угловой радиус), R – экваториальный радиус Земли, ρ0– горизонтальный параллакс светила.
17. Расстояние до звезд:
в парсеках: , где – годичный параллакс звезды, выраженный в радианах;
в астрономических единицах: , где – годичный параллакс звезды, выраженный в секундах дуги;
в километрах: , где – годичный параллакс звезды, выраженный в секундах дуги, a – средний радиус (большая полуось) земной орбиты.
18. Связь блеска звезды и ее звездной величины (формула Погсона):
, где I1 – освещенность, создаваемая звездой, звездная величина которой равна m1, и I2 – освещенность, создаваемая другой звездой, звездная величина которой равна m2.
19. Абсолютная звездная величина:
, где m – видимая звездная величина, R – расстояние до звезды в парсеках.
20. Закон Стефана–Больцмана:
ε=σT4, где ε – энергия, излучаемая в единицу времени с единицы поверхности, Т – температура (в кельвинах), а σ – постоянная Стефана–Больцмана.
21. Закон Вина:
, где λmax – длина волны, на которую приходится максимум излучения абсолютно черного тела (в сантиметрах), Т – абсолютная температура в кельвинах.
22. Закон Хаббла:
, где v – лучевая скорость удаления галактики, c – скорость света, Δλ – доплеровское смещение линий в спектре, λ – длина волны источника излучения, z – красное смещение, r – расстояние до галактики в мегапарсеках, H – постоянная Хаббла, равная 75 км / (сМпк).
4





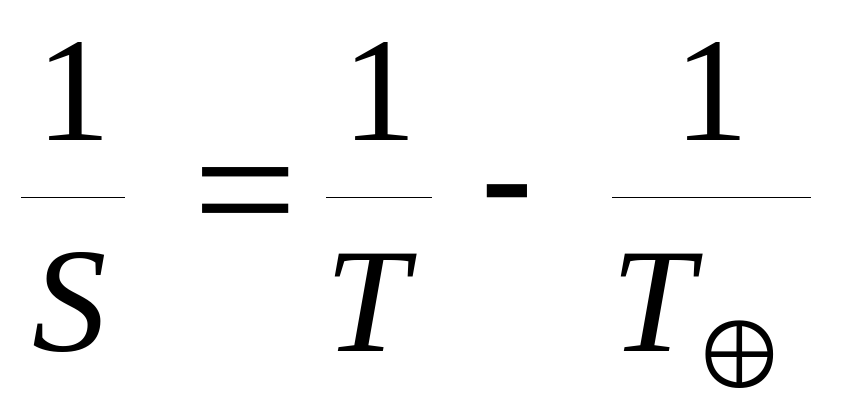 , где T – звездный период обращения Земли вокруг Солнца.
, где T – звездный период обращения Земли вокруг Солнца.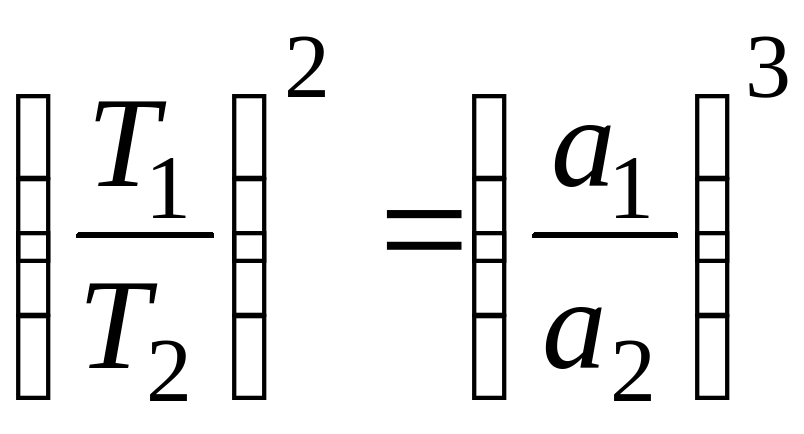 , где Т1 и Т2 – периоды обращения планет, a1 и a2 – большие полуоси их орбиты.
, где Т1 и Т2 – периоды обращения планет, a1 и a2 – большие полуоси их орбиты.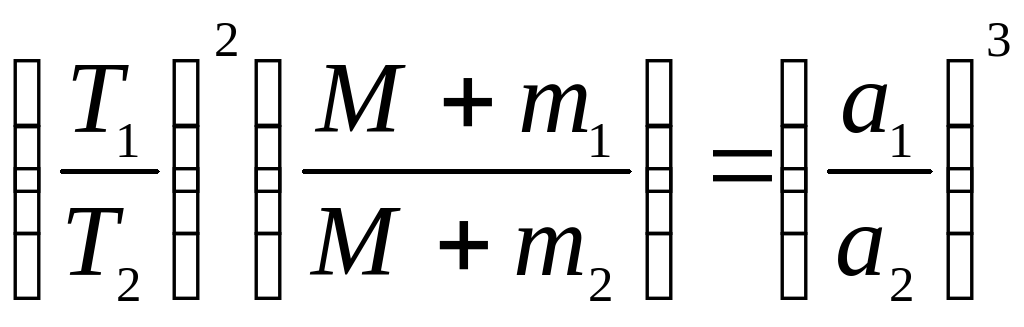 , где Т1 и Т2 – сидерические (звездные) периоды обращения планет, М – масса Солнца, m1 и m2 – массы планет, a1 и a2 –большие полуоси орбит планет;
, где Т1 и Т2 – сидерические (звездные) периоды обращения планет, М – масса Солнца, m1 и m2 – массы планет, a1 и a2 –большие полуоси орбит планет;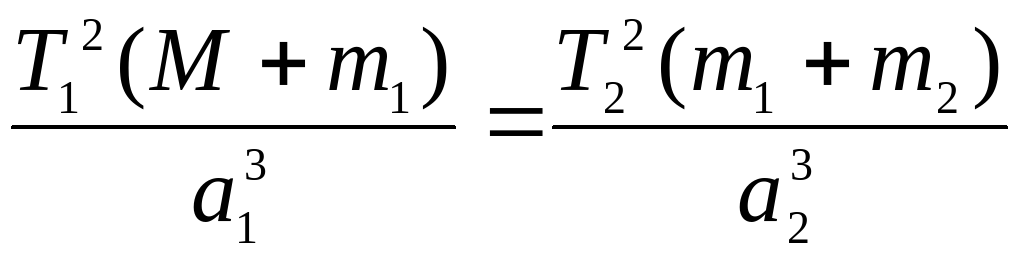 , где M – масса Солнца; m1 – масса планеты; m2 – масса спутника планеты; Т1 и a1 – период обращения планеты вокруг Солнца и большая полуось ее орбиты; Т2 и a2 – период обращения спутника вокруг планеты и большая полуось его орбиты;
, где M – масса Солнца; m1 – масса планеты; m2 – масса спутника планеты; Т1 и a1 – период обращения планеты вокруг Солнца и большая полуось ее орбиты; Т2 и a2 – период обращения спутника вокруг планеты и большая полуось его орбиты;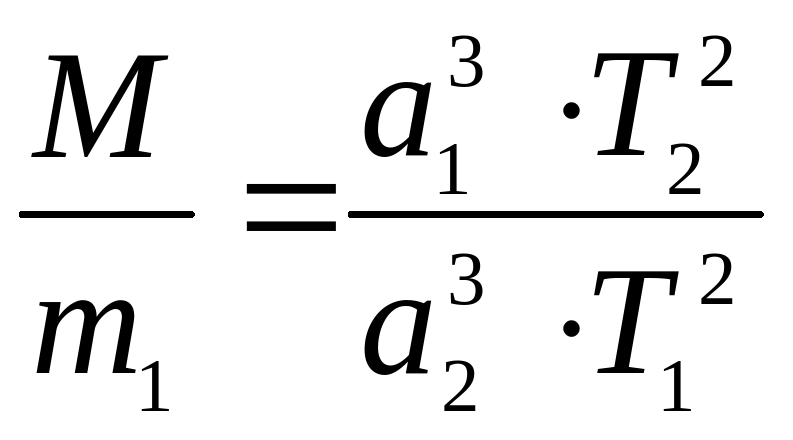 .
.









