Открытый урок "Линейное уравнение с двумя переменными"

Этап

Деятельность учителя

Мотивация к деятельности

Цель этапа: включение учащихся в деятельность.

2 мин

– Здравствуйте, ребята! Здравствуйте, уважаемые гости нашего урока!

Дорогие ребята, сегодня у нас не совсем обычный урок, но, как всегда, мне понадобится ваше внимание и трудолюбие. Давайте сделаем небольшое упражнение.

Слайд 1 Таблица. Сосредоточились! Запомните эту таблицу, смотрите на нее, охватывая взглядом все сразу. (5 секунд) А теперь скажите, сколько в ней единиц?- (-)- а четверок? - Очень хорошо.

Сегодня мы будем общаться на самом универсальном языке во Вселенной- и это язык …?( математики)

Слайд 2

Мне бы хотелось, чтобы у нас сегодня состоялся разговор, ибо как сказал Вовенарг : «Непринужденная беседа — лучшая школа для ума». Хочется еще, чтобы вы помнили слова российского историка Ключевского: «Есть люди, которые умеют говорить, но не умеют ничего сказать. Это ветряные мельницы, которые вечно машут крыльями, но никогда не летают». Надеюсь, что нам сегодня удастся взлететь на вершину новых знаний алгебры.

МОТИВАЦИЯ!

Актуализация и пробное учебное действие

Цель этапа: подготовка мышления учащихся и организация осознания ими внутренней потребности к построению нового способа действий.

6 мин

- Как вы думаете, может ли алгебра понадобиться, например, в парикмахерской? Оказывается, что такие случаи бывают. Послушаем разговор, который там (довольно давно) однажды состоялся. (Звучит запись разговора):

Учитель: - А вы смогли бы помочь эти мастерам?

Задачу можно решить и арифметически. Но язык алгебры приводит здесь к успеху проще и быстрее

Переведем эту задачу с родного языка на язык алгебры привычным нам табличным способом: таблица в Рабочем листе, заполним ее.

Слайд 3

Слайд 4. Составим уравнение: 0,3x + 0,03y = 0,12(x + y)

Что же это за алгебраический объект у нас получился? Попробуем дать ему название.

(уравнение) (с двумя переменными)

ПРОБЛЕМНАЯ ЗАДАЧА

Постановка учебной задачи

Цель этапа: обсуждение затруднений (почему возникли затруднения, что мы еще не знаем).

3 мин

Это линейное уравнение с двумя переменными.

Сформулируем тему урока. (Линейное уравнение с двумя переменными)

Цель нашего урока – знакомство с линейными уравнениями с двумя переменными.

Чтобы вам хотелось узнать сегодня на уроке?

( листы на доску)

Задачи урока:

1.Что называется линейным уравнением с двумя переменными?- опр.

2.Что называется решением уравнения с двумя переменными?-( пара чисел)

3.Как решить линейное уравнение с двумя переменными?- подбором.

ЦЕЛИ И ЗАДАЧИ УРОКА

Выявление места и причины затруднения

Цель этапа: постановка учебной деятельности и на этой основе- выбора способа и средств их реализации

10 мин

А) Нам ведь уже знакомы похожие объекты? Что это за объекты? (линейные уравнения с одной переменной)

Придумайте и запишите линейное уравнение с одной переменной. Слушаю.

-Посмотрите на доску, перед нами действительно линейное уравнение с одной переменной. Вспомним общий вид линейного уравнения с одной переменной.

(ax=b, где a и b –некоторые числа, а x-переменная).

А как определить общий вид линейного уравнения с двумя переменными?

Перед вами на доске уравнения

1. 3у+2х=0.

2. 5у – 6 =0.

3. 0,2х² – у +3=0.

4. х+у=15.

5. 4х – 17 = 0.

6. 5х+2у=12

Работаем в парах.

Выпишите те уравнений, которые бы вы отнесли к линейным уравнениям с двумя переменными? Проверьте себя и своего партнера. Запишите общий вид уравнения, заменив числовые коэффициенты на буквы а, в, с. Обменялись РЛ и поставили плюс или минус.

Определим общий вид линейного уравнения с двумя переменными: (ax+by=c, где a,b,c некоторые числа, x, y переменные.)

Попробуйте сформулировать определение:

(Линейным уравнением с двумя переменными называется уравнение вида ax+by=c, где a,b,c некоторые числа, x, y переменные)—проговариваем.

Возьмите теоретический справочник. Прочитайте определение про себя. Не ошиблись ли мы в определении. Есть ли различия?

Придумайте и запишите в рабочем листе свое линейное уравнение с двумя переменными.-( 1.Что называется линейным уравнением с двумя переменными?- ответили, лист переворачиваю)

Б) Как решаются и свойства

Вернемся к линейным уравнениям с одной переменной. Давайте вспомним, как они решаются, и решим уравнение с объяснением:

2х+6=10

(Перенесем слагаемое без х в правую часть уравнения, изменив при этом его

знак на противоположный: 2х=10-6 , вычислим результат 2х=4. Разделим обе

части уравнения на 2, получим х=2).

- Ребята, такие уравнения вы хорошо умеете решать.

Вспомним алгоритм решения.

- А какие свойства применяли при решении этих уравнений? (Если в уравнении слагаемое перенести из одной части в другую, изменив его знак, то получится уравнение, равносильное данному.)

- А какое еще свойство вы применяли? (Если разделить или умножить обе части уравнения на одно и тоже отличное от нуля число, то получится уравнение равносильное данному.)

Линейные уравнения с двумя переменными обладают такими же свойствами.

Для уравнений с двумя переменными все остается в силе. Загляните в справочный лист и прочитайте свойства линейного уравнении с двумя переменными.

В) Решим конкретное уравнение

Ребята, ведь мы забыли про мастеров из парикмахерской. Это нехорошо. Надо им помочь. Давайте вернемся к той ситуации. Применим свойства уравнений с двумя переменными к полученному нами уравнению, и сведем его к виду, указанному в определении.

0,3x + 0,03y = 0,12(x + y)- что делаем?

0,3x + 0,03y = 0,12x + 0,1-группируем неизвестные справа и слева.

0,3x – 0,12x = 0,12y – 0,03y- приводим подобные

0,18x - 0,09y =0- умножаем на 100( переход к целым числам)

18x - 9y=0

2x-y=0

При каких значениях x и y наше уравнение обратится в верное равенство?

при х=1, у=2 (записываю на доске) (2∙1=2)

Ребята, ведь мы забыли про мастеров из парикмахерской. Это нехорошо. Надо им помочь. Давайте вернемся к той ситуации. Применим свойства уравнений с двумя переменными к полученному нами уравнению, и сведем его к виду, указанному в определении.

0,3x + 0,03y = 0,12(x + y)- что делаем?

0,3x + 0,03y = 0,12x + 0,1-группируем неизвестные справа и слева.

0,3x – 0,12x = 0,12y – 0,03y- приводим подобные

0,18x - 0,09y =0- умножаем на 100( переход к целым числам)

18x - 9y=0

2x-y=0

При каких значениях x и y наше уравнение обратится в верное равенство?

при х=1, у=2 (записываю на доске) (2∙1=2)

Что же является решением линейных уравнений с двумя переменными? (Решением уравнения с двумя переменными называется пара значений переменных, обращающая это уравнение в верное равенство.)

Прочитайте это определение в справочнике про себя. Не ошиблись ли мы, давая определение?-( ответили 2.Что называется решением уравнения с двумя переменными?-0 лист переворачиваю)

А какие еще пары чисел будут являться решениями уравнения 2x-y=0?

х=2, у=4

х=3, у=6

х=4, у=8

Сколько же таких пар? (Множество)

В нашем случае это будут числа, одно из которых в два раза больше другого.

Т.е 3-процентного раствора надо взять вдвое больше, чем 30-процентного. Как же смешать? мерить будем мерным стаканчиком. Дети показывают на практике:

Выходит ученик , наливает 100 г 3% раствора и 50 г 30% раствора.

Мы решили задачу!- а как? Подбором чисел.

1.Общий вид ур-я

( по аналогии)

-на доске

2.Свойства – через

повторение

Уравнений с одной

Переменной

3.Решение уравнения

Проблемной задачи

Интерпретация

Первичное закрепление.

Цель этапа: усвоение учащимися правила

3 мин

Физминутка

3 минуты

Продолжим знакомство с линейными уравнениями.

Присмотритесь, пожалуйста, к этим парам. Может есть у кого предложение, как записать это решение короче, пользуясь символическим языком математики?

( (2, 4), (3,6), (4, 8) и т.д.- парами

-При такой записи необходимо знать, значение какой из переменных стоит на первом месте, а какой – на втором. В записи решений уравнения с переменными х и у на первом месте записывают значения х, а на втором – значение у.

Где-то нам уже встречалась такая запись? Правильно, это координаты точек на координатной плоскости.

Есть ли у нашего уравнения еще решения? Сколько же у него решений? (бесконечно много)

Можем ли мы все его решения нанести на координатную плоскость? (да, они образуют прямую). Все ли решения будут пригодны для ситуации в парикмахерской?- (нет)

Переворачиваю 3 лист.(3.Как решить линейное уравнение с двумя переменными?- подбором. )

На основании построенного графика сделаем вывод о количестве решений линейного уравнения с двумя переменными (множество решений уравнения с двумя неизвестными, как правило, бесконечно и его изображение на координатной плоскости — прямая линия, а также может быть и пустым)

Общий вид- решение

в координатной форме

Самостоятельная работа с самопроверкой по эталону

Цель этапа: самооценка учащимися результатов своей учебной деятельности

8 мин

Организует деятельность по применению новых знаний

Работа в парах

1.Среди данных уравнений выберите линейные уравнения с двумя переменными:

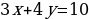
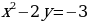
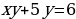
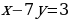
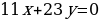
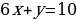2.Является ли решением уравнения пара чисел

1. 5(3;-8)

2. (2;4)

3. (0;10)

4. (-2;2)

3.Составьте уравнение и найдите хотя бы одно решение

Задача: Сахар расфасован в пакеты по 3 кг и по 2 кг. Сколько пакетов каждого вида надо взять, чтобы получить 20 кг сахара?

4.Изобразить решения линейного уравнения х+у-3=0 точками в координатной плоскости

Рефлексия деятельности

3 мин

Организует рефлексию, организует самооценку результатов уч-ся.

1.Какую проблему мы поставили на уроке?( как решить задачу с двумя неизвестными)

2.Мы выполнили задачи этого урока? Какие? ( на доске)

3. Что мы повторили? ( Решение линейных уравнений с одним неизвестным, алгоритм)

4.Где еще можно будет применить уравнения с двумя неизвестными? ( в различных задачах)

5.Выберите яблоко

Вы можете написать на яблоке свои впечатления, вопросы, пожелания. В конце урока прикрепите его к дереву математики.