Открытый урок по теме: "Треугольник. Решение задач"

Урок геометрии в 7 «Б» классе

Подготовил: учитель математики МКОУ СОШ № 9 с. Воздвиженское, Апанасенковского района, Ставропольского края, Скиба Ольга Юрьевна.

Тема урока: Решение задач по теме «Треугольник» (слайд 1).

Тип урока: урок обобщения и систематизации знаний.

Цели урока:

1. Систематизировать и обобщить знания,

умения и навыки по применению признаков равенства треугольников;

2. Подготовиться к контрольной работе

3. Развивать логическое мышление, речь, память, реакцию, фантазию;

4. Показать применение треугольников в быту и жизни;

5. Воспитывать общую культуру, активность, самостоятельность, умение общаться.

ХОД УРОКА

1. Организационный момент (слайд 2).

Один мудрец сказал: "Высшее проявление духа - это разум. Высшее проявление разума - это геометрия.

Клетка геометрии - это треугольник. Он также неисчерпаем как Вселенная. Душа геометрии - окружность.

Познайте окружность и треугольник, и вы не только познаете  душу геометрии, но и  возвысите свой разум".

1. Сообщение темы и целей урока.

Сегодня мы продолжаем разговор об основной клетке геометрии – треугольнике.

При подведении итога урока мы с вами должны ответить на основополагающий вопрос урока:

Чем удивителен треугольник? (слайд 3).

1. Теоретическая разминка.

- Как вы думаете, на какие вопросы вы должны знать ответ, изучая тему «Треугольник»?

(2 ученика работают по карточкам у доски).

Карточка 1. (слайд 4).

1. Из вершины N к основанию MK равнобедренного треугольника MNK провели биссектрису и медиану. Сколько отрезков провели в треугольнике?

2. Какой из элементов – медиана, биссектриса, высота – всегда лежит внутри треугольника?

3. Треугольник с вершинами в точках A, B, C равен треугольнику с вершинами в точках K, L, M, 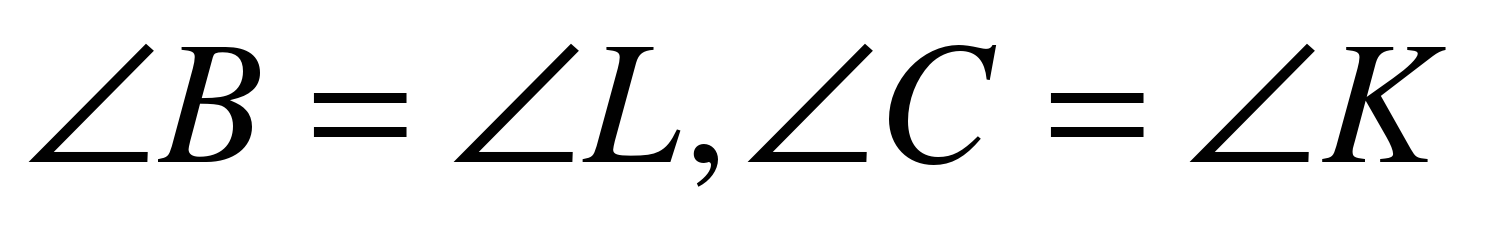. Назовите пары равных сторон.

Карточка 2. (слайд 5).

1. Могут ли две высоты треугольника совпадать с его сторонами?

2. Могут ли два каких – либо угла треугольника иметь разные величины, если все его стороны равны?

3. В равнобедренном треугольнике CDE с основанием DE проведена медиана CM. Назовите пары равных углов.

(2 ученика работают по карточкам на местах с самопроверкой (слайд 6).).

Тест 1.

- Назовите …

• Основные элементы треугольника (вершины, стороны, углы)

• Виды треугольников по углам,

• Виды треугольников по сторонам,

• Сумма углов треугольника,

• Вертикальные углы, их свойства,

• Смежные углы, их свойства,

• Равнобедренный треугольник, его свойства,

• Медианы, биссектрисы, высоты, их свойства,

• Признаки равенства треугольников.

- Что является важным при решении задач? (знание определений и теорем)

- Умение применять теоретические знания при решении задач.

1. Решение задач с практическим содержанием.

- Треугольник — это простейшая фигура: три стороны и три вершины. Математики его называют двумерным симплексом. «Сим­плекс» по-латыни означает простейший. Именно в силу своей про­стоты треугольник явился основой многих практических измерений. Землемеры при своих вычисле­ниях площадей земельных участков и аст­рономы при нахождении расстояний до пла­нет и звезд используют свойства треуголь­ников.

(слайд 7).

Теореме о равенстве треугольников древнегреческий ученый Фалес Милетский нашел практическое применение.

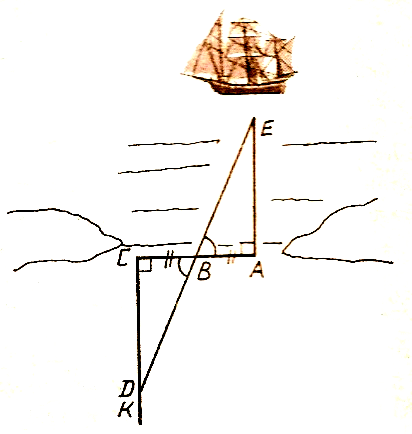
В гавани Милета был построен дальномер, определяющий расстояние до корабля в море. Он представлял собой три вбитых колышка А, В, С, (АВ = ВС) и размеченную прямую . При появлении корабля на прямой СК находили точку D такую, чтобы точки D, В, Е оказывались на одной прямой. Как ясно из чертежа, расстояние на земле СD и является искомым расстоянием до корабля АЕ по воде.

Какой признак равенства треугольников был использован?

Задача 1. В мастерской сделаны из проволоки стержни длиной 2 дм, 5 дм, 9 дм, 11 дм, 17 дм. Выясните, из каких стержней, соединяя их концы, можно сделать треугольные конструкции, а из каких нельзя.

Можно: 5 дм, 9 дм, 11 дм; 5 дм, 9 дм, 17 дм. Нельзя из всех остальных сочетаний по 3 стержня. (слайд 8).

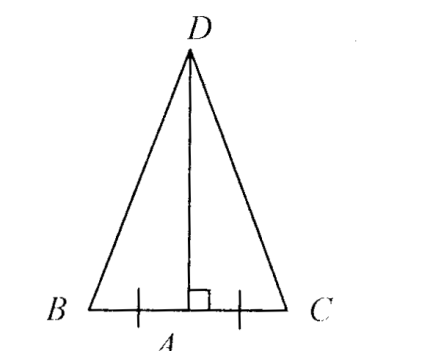
Задача 2. Населенные пункты А, В, С, D расположены так, что пункт А находится в нескольких километрах к югу от D, а пунк­ты В и С— на одинаковых расстояниях к западу и востоку (соот­ветственно) от А. Верно ли, что В и С находятся на одинаковом расстоянии от D?

Решение. Треугольники DАВ и DАС равны по двум сторонам и углу между ними, значит, ВD = СD. (слайд 9).

VI. Физкультминутка.

Быстро встали, улыбнулись,

Выше-выше подтянулись.

Ну-ка плечи распрямите,

Поднимите, опустите.

Вправо, влево повернитесь,

Рук коленями коснитесь.

Сели, встали, сели, встали,

И на месте побежали.     

VII. Работа в группах (разноуровневые карточки).

Карточка 1. Уровень «3».

Карточка 2. Уровень «4».

1.

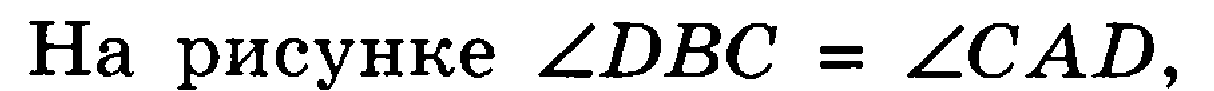
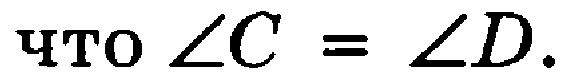
Карточка 3. Уровень «5».

1. Применение изучаемой темы в природе.

- При изучении данной темы вы познакомились с понятием треугольника. Знакомый всем нам треугольник таит в себе немало интересного и загадочного.

В ходе изучения темы вам были заданы проблемные вопросы, на которые вы должны были найти ответы:

1. Что же это такое, загадочный Бермудский треугольнике, в котором бесследно исчезают корабли и самолёты? (слайд 12).

2. Что такое «флексагон», фокусы с ним. (слайд 13).

Послушаем тех, кто подготовил сообщения по данным вопросам.

(выступление учащихся)

- Хочу добавить, что треугольник был незаменим во время Великой Отечественной войны. Сейчас письма мы отправляем в прямоугольных конвертах, а раньше, во время войны, письма имели треугольную форму.
(слайд 14 - 15).

Солдатский треугольник – письмо без марки и конверта, отправленное солдатом с фронта или солдату на фронт. Я научу вас складывать треугольное письмо. Перед написанием письма надо было сложить треугольник из чистого листа. Обычно это был страничный листик из школьной тетрадки.

1. Рефлексия.

- Раскройте ваши треугольные конверты и напишите мне, что вам понравилось на уроке, а что не понравилось

1. Подведение итогов, домашнее задание.

- Ответим на основополагающий вопрос нашего урока: Чем удивителен треугольник? (слайд 16).

- Конечно, все законы красоты невозможно вместить в несколько фраз и формул, но, изучая математику, мы можем открыть новые элементы прекрасного, которые находят свое применение в окружающем нас мире. Я думаю, что и в дальнейшем людей будут интересовать треугольники. И из таких простых слагаемых, может быть кто-нибудь из вас, составит ещё более интересную, более сложную, более многогранную сумму и назовет это новое чудо природы еще более интересным и замечательным словом.

Подошло время подводить итоги урока и задавать домашнее задание.

VIII. Домашнее задание (слайд 17): подготовиться к контрольной работе;

на выбор:

1) как измерить ширину озера. № 169, с.52

2) Придумать и решить практическую задачу, в которой бы использовались свойства или признаки равенства треугольников.