Платоновы и архимедовы тела

Информационный лист 2

Платоновы и архимедовы тела

Многогранник – это тело, граница которого состоит из конечного числа многоугольников.

У многогранника различают вершины, ребра и грани.

Обозначим число вершин, ребер и граней многогранника буквами v, e и f соответственно. В примерах на Рис. 1. вы видите многогранники (Платоновы тела) с различными значениями чисел v, e и f. Эти числа не могут

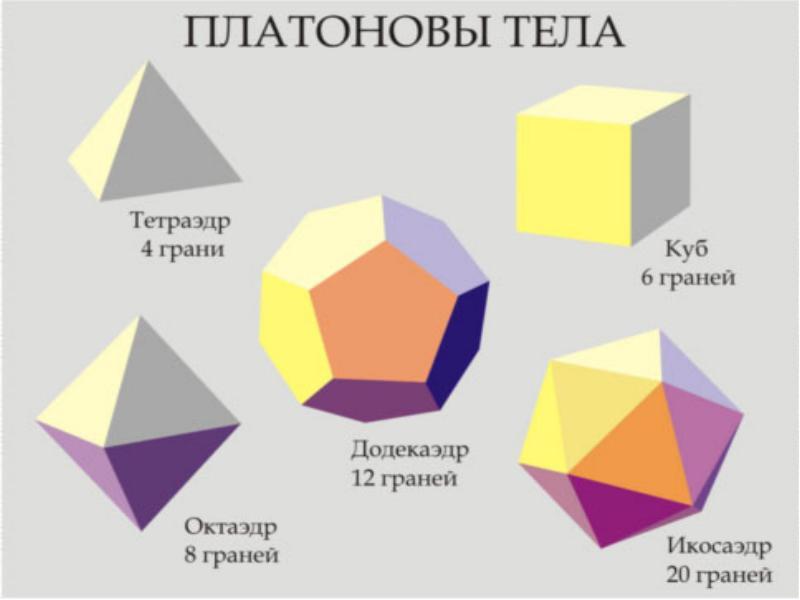
Рис. 1

быть какими угодно. Ясно, что v4, e6 и f4.

Между числами v, e и f существует глубокая связь. Великий математик Леонард Эйлер заметил, что для обширного класса многогранников, в который входят, в частности, все выпуклые многогранники, выполняется простое соотношение (теорема Эйлера): χ=v−e+f=2. Эта константа χ (греческая буква χ читается как хи) называется характеристикой Эйлера – Пуанкаре. Заметьте, что не для всех многогранников она равна 2, но в то же время она может быть равна 2 не только для выпуклых многогранников.

Многогранники издревле привлекали внимание ученых – математиков, физиков и философов. Почти две с половиной тысячи лет тому назад великий греческий философ Платон в диалоге «Тимей» описал систематическое построение космоса и представил все реально существующее как совокупное взаимодействие космических идей и материи.

С четырьмя главными земными сущностями – землей, огнем, водой и воздухом – Платон сопоставляет прекрасные геометрические тела, построения которых он подробно описывает. Вот несколько цитат из произведения Платона.

«Когда же четыре равносторонних треугольника окажутся соединенными в три двугранных угла, они образуют один объемный угол... Завершив построение четырех таких углов, мы получаем первый объемный вид, имеющий свойство делить всю описанную около него сферу на равные и подобные части.

Второй вид строится из исходных треугольников, соединившихся по восемь в равносторонний треугольник и образующих каждый раз из четырех плоских углов по одному объемному; когда таких объемных углов шесть, второе тело получает завершенность.

Третий вид образуется... из двенадцати объемных углов, каждый из которых охвачен пятью равносторонними треугольниками, так что все тело имеет двадцать граней...»

Так Платоном описаны правильный тетраэдр, октаэдр и икосаэдр.

«Земле мы, конечно, припишем вид куба: ведь из всех четырех сущностей наиболее неподвижна и пригодна к образованию тел именно Земля, а потому ей необходимо иметь самые устойчивые основания... Из всех тел наиболее подвижно по природе своей то, у которого наименьшее число оснований, ибо оно со всех сторон имеет режущие грани и колющие углы... Пусть же образ пирамиды, рожденный объемным, и будет первоначалом и семенем огня...»

Далее столь же образно Платон связывает воздух с октаэдром, а воду с икосаэдром. Что же касается пятого правильного многогранника – додекаэдра, то Платон говорит, что у него «в запасе оставалось еще пятое многогранное построение: его Бог определил для Вселенной и прибегнул к нему, когда разрисовывал ее и украшал».

Пять правильных многогранников – тетраэдр, куб, октаэдр, икосаэдр и додекаэдр – остаются символом глубины и стройности геометрии, образцом красоты и совершенства.

Другой великий греческий ученый – Архимед – получил замечательные результаты при вычислении объемов многогранников и других геометрических тел. Архимед описал большую серию симметричных многогранников, называемых архимедовыми телами (рис. 2).

Рис. 2. Архимедовы тела

Платоновы и архимедовы тела имеют богатую симметрию. В природе похожую симметрию имеют различные кристаллы. Атомы кристалла расположены в пространстве очень симметрично. Их взаимное расположение в пространстве может неограниченно повторяться. Наука о кристаллах – кристаллография – поставила перед математиками вопрос: какие вообще возможны типы симметрий кристаллов? Эта задача была успешно решена к середине XX века. Большую роль в ее решении Федоров. Оказалось, что существует ровно 230 типов симметрий, что позволило составить полный список всех возможных типов кристаллов и реализовать на практике их создание.

Многие вопросы о многогранниках были решены лишь недавно, а некоторые из них остаются открытыми до сих пор. Выдающийся вклад в теорию многогранников и развитие математического образования в нашей стране внес замечательный русский математик Александр Данилович Александров.

1