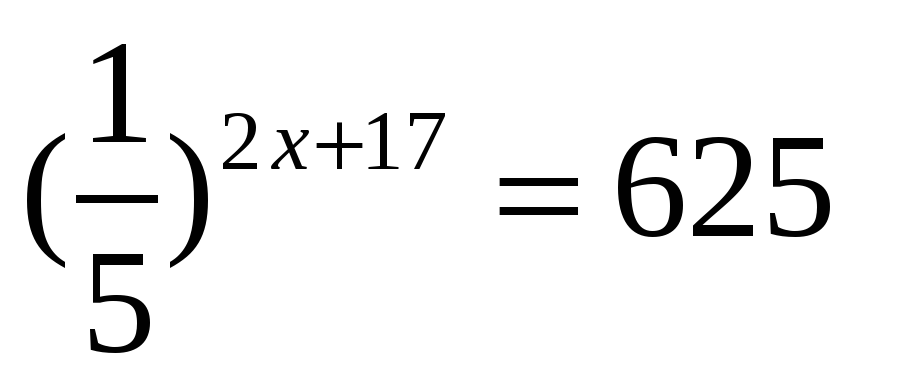МАТЕМАТИКА, 11 класс Вариант № 1, Апрель 2019
Тьюторская диагностическая работа по МАТЕМАТИКЕ
ВАРИАНТ № 1
Инструкция по выполнению работы
На выполнение краевой диагностической работы по математике дается 90 минут. Работа состоит из двух частей, включающих в себя 12 заданий.
Часть 1 содержит 12 заданий (задания 1–12) базового уровня сложности, проверяющих наличие практических математических знаний и умений.
Ответом к каждому из заданий 1–12 является целое число или конечная десятичная дробь.
.
Бланк ответов заполняется яркими чёрными чернилами. Допускается использование гелиевой, капиллярной или перьевой ручки.
При выполнении заданий Вы можете пользоваться черновиком. Обращаем Ваше внимание, что записи в черновике не будут учитываться при оценивании работы.
Желаем успеха!
Часть 1
| Ответом на задания 1–12 должно быть целое число или конечная десятичная дробь. Ответ следует записать в бланк ответов № 1 справа от номера выполняемого задания, начиная с первой клеточки. Каждую цифру, знак минус и запятую пишите в отдельной клеточке в соответствии с приведёнными в бланке образцами. Единицы измерений писать не нужно. Если ответом является последовательность цифр, то запишите эту последовательность в бланк ответов № 1 без пробелов, запятых и других дополнительных символов. |
1. Среднее гармоническое трёх чисел  и
и  вычисляется по формуле
вычисляется по формуле  . Найдите среднее гармоническое чисел
. Найдите среднее гармоническое чисел  и
и  .
.
Ответ:________________________________
2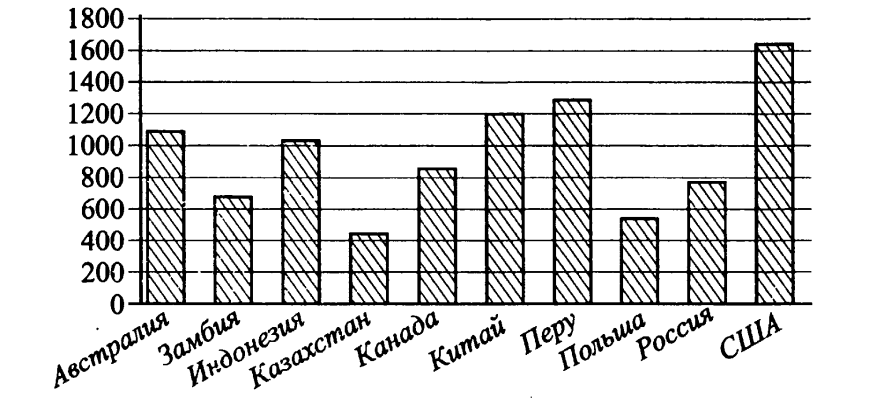 . На диаграмме показано распределение выплавки некоторого металла в 10 странах мира (в тысячах тонн) за 2006 год. Среди представленных стран первое место по выплавке этого металла занимали США, десятое место – Казахстан. Какое место занимал Китай?
. На диаграмме показано распределение выплавки некоторого металла в 10 странах мира (в тысячах тонн) за 2006 год. Среди представленных стран первое место по выплавке этого металла занимали США, десятое место – Казахстан. Какое место занимал Китай?
Ответ:________________________
3. Сергей Петрович хочет купить в интернет-магазине микроволновую печь определённой модели. В таблице показано 6 предложений от разных интернет-магазинов.
| Номер магазина | Рейтинг магазина | Стоимость товара (руб.) | Стоимость доставки (руб.) |
| 1 | 3 | 12 895 | 400 |
| 2 | 5 | 18 490 | 0 |
| 3 | 5 | 13 513 | 0 |
| 4 | 5 | 13 745 | 390 |
| 5 | 4 | 13 411 | 399 |
| 6 | 4 | 17 489 | 0 |
Сергей Петрович считает, что покупку нужно делать в магазине, рейтинг которого не ниже 4. Среди магазинов, удовлетворяющих этому условию, выберите предложение с самой низкой стоимостью покупки с учётом доставки.
В ответе запишите номер выбранного магазина.
Ответ: ___________________________
4. Вектор  с началом в точке А (3;6) имеет координаты (9;3). Найдите сумму координат точки В.
с началом в точке А (3;6) имеет координаты (9;3). Найдите сумму координат точки В.
Ответ: ____________________________
5. У Кати в копилке лежит 7 однорублевых, 6 двухрублевых и 3 пятирублевых монеты. Катя наугад достает из копилки одну монету. Найдите вероятность того, что оставшаяся после этого в копилке сумма составит более 30 рублей.
Ответ: __________________________
6. Решите уравнение: 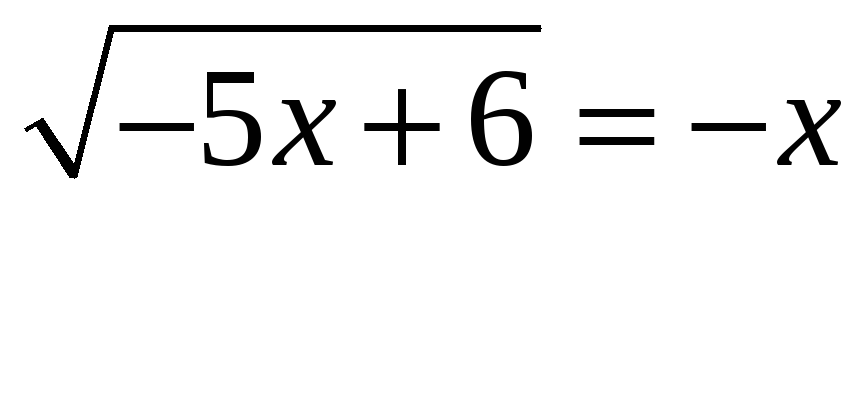 . Если уравнение имеет более одного корня, найдите больший из них.
. Если уравнение имеет более одного корня, найдите больший из них.
Ответ:_______________________________
7. Стороны основания правильной шестиугольной пирамиды равны 20, боковые рёбра равны 25. Найдите объём этой пирамиды, в ответе укажите 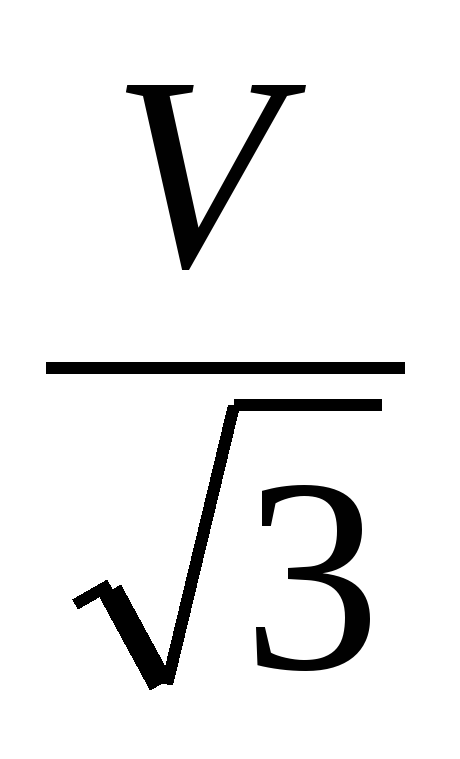 .
.
О твет:_______________________________
твет:_______________________________
8. На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Ответ:__________________________________
9. Одна цилиндрическая кружка вдвое выше второй, зато вторая в два раза шире. Найдите отношение объема второй кружки к объему первой.
Ответ:_________________________________
10. Упростите выражение: � � (�
� (� �- 2(sinx+1)
�- 2(sinx+1)
Ответ:__________________________________
11. Поезд, двигаясь равномерно со скоростью 70 км/ч, проезжает мимо лесополосы, длина которой равна 800 метров, за 1 минуту 30 секунд. Найдите длину поезда в метрах. Ответ:_________________________________
12. Найдите наименьшее значение функции 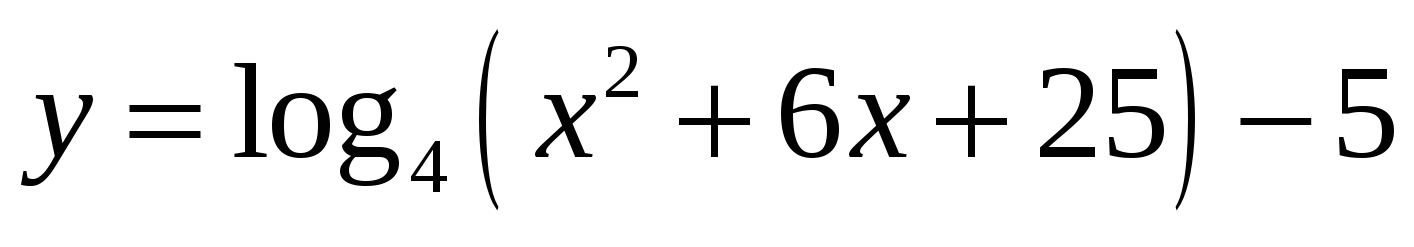
Ответ:_________________________________
Тьюторская диагностическая работа по МАТЕМАТИКЕ
ВАРИАНТ № 2
На выполнение краевой диагностической работы по математике дается 90 минут. Работа состоит из двух частей, включающих в себя 12 заданий.
Часть 1 содержит 12 заданий (задания 1–12) базового уровня сложности, проверяющих наличие практических математических знаний и умений.
Ответом к каждому из заданий 1–12 является целое число или конечная десятичная дробь.
.
Бланк ответов заполняется яркими чёрными чернилами. Допускается использование гелиевой, капиллярной или перьевой ручки.
При выполнении заданий Вы можете пользоваться черновиком. Обращаем Ваше внимание, что записи в черновике не будут учитываться при оценивании работы.
Желаем успеха!
Часть 1
| Ответом на задания 1–12 должно быть целое число или конечная десятичная дробь. Ответ следует записать в бланк ответов № 1 справа от номера выполняемого задания, начиная с первой клеточки. Каждую цифру, знак минус и запятую пишите в отдельной клеточке в соответствии с приведёнными в бланке образцами. Единицы измерений писать не нужно. Если ответом является последовательность цифр, то запишите эту последовательность в бланк ответов № 1 без пробелов, запятых и других дополнительных символов. |
1.Площадь треугольника со сторонами 
 и
и  можно найти по формуле Герона
можно найти по формуле Герона  , где
, где  . Найдите площадь треугольника со сторонами
. Найдите площадь треугольника со сторонами  ,
,  ,
,  .
.
Ответ:________________________________
2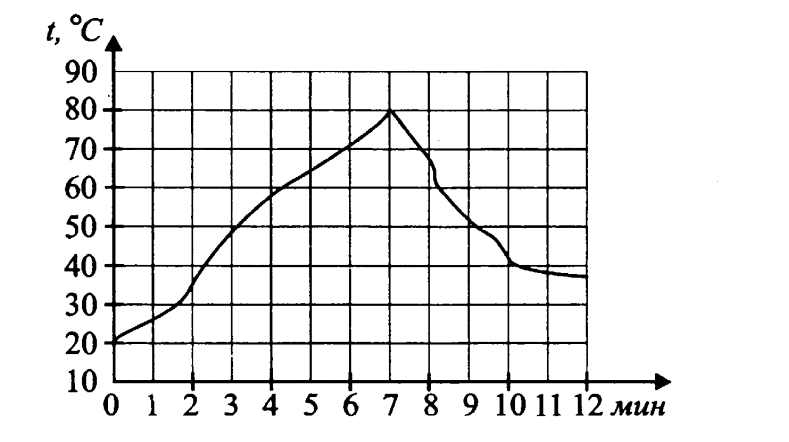 . На графике показан процесс разогрева двигателя легкового автомобиля при температуре окружающего воздуха 15 0 С. На оси абсцисс откладывается время в минутах, прошедшее от запуска двигателя, на оси ординат – температура двигателя Цельсия. Когда температура достигает определённого значения, включается вентилятор, охлаждающий двигатель, и температура начинает понижаться. Определите по графику, сколько минут прошло от момента запуска двигателя до включения вентилятора?
. На графике показан процесс разогрева двигателя легкового автомобиля при температуре окружающего воздуха 15 0 С. На оси абсцисс откладывается время в минутах, прошедшее от запуска двигателя, на оси ординат – температура двигателя Цельсия. Когда температура достигает определённого значения, включается вентилятор, охлаждающий двигатель, и температура начинает понижаться. Определите по графику, сколько минут прошло от момента запуска двигателя до включения вентилятора?
Ответ: ______________________________
3. В городском парке имеется пять аттракционов: карусель, колесо обозрения, автодром, «Ромашка» и «Весёлый тир». В кассах продаётся шесть видов билетов, каждый из которых позволяет посетить один или два аттракциона. Сведения о стоимости билетов представлены в таблице.
| Номер билета | Набор аттракционов | Стоимость (руб.) |
| 1 | «Весёлый тир», колесо обозрения | 500 |
| 2 | Карусель, «Ромашка» | 350 |
| 3 | Карусель, колесо обозрения | 150 |
| 4 | Автодром, «Весёлый тир» | 500 |
| 5 | «Ромашка» | 250 |
| 6 | Автодром, “Ромашка” | 450 |
Какие билеты должен купить Андрей, чтобы посетить все пять аттракционов и затратить 900 рублей?
В ответе укажите какой-нибудь один набор номеров билетов без пробелов, запятых и других дополнительных символов.
Ответ: _______________________________
4. Вектор  с концом в точке В (5;3) имеет координаты (3;1). Найдите сумму координат точки А.
с концом в точке В (5;3) имеет координаты (3;1). Найдите сумму координат точки А.
Ответ: _______________________________
5. В женском спринте на этапе кубка мира по биатлону участвуют 80 спортсменок, среди которых 6 биатлонисток из России. Порядок старта определяется жеребьевкой. Найдите вероятность того, что пятнадцатой будет стартовать спортсменка из России.
Ответ: ________________________________
6. Решите уравнение: 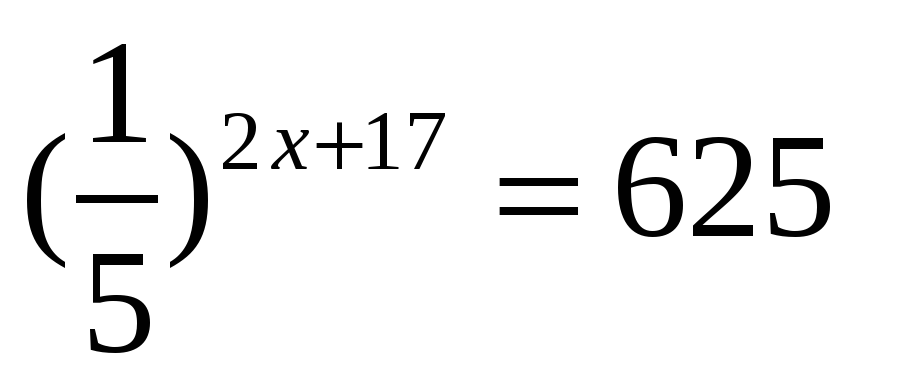
Ответ:__________________________________
7. Найдите объём правильной треугольной пирамиды, если её апофема равна  и наклонена к плоскости основания под углом .
и наклонена к плоскости основания под углом .
Ответ:__________________________________
8. На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Ответ:__________________________________
9. Одна цилиндрическая кружка вдвое выше второй, зато вторая в два раза шире. Найдите отношение объема первой кружки к объему второй.
Ответ:_________________________________
10. Упростите выражение: (sinx+cosx)2-sin2x
Ответ:__________________________________
11. Маша спустилась по движущемуся вниз эскалатору за 36 секунд. По неподвижному эскалатору с той же скоростью относительного него она спустится за 1 минуту 3 секунды. За сколько секунд она спустится, стоя на ступеньках движущегося эскалатора
Ответ:_________________________________
12. Найдите наименьшее значение функции y=7+12x-x3 на отрезке [ -2; 2]
Ответ:_________________________________
Краевая диагностическая работа по МАТЕМАТИКЕ
ВАРИАНТ № 3
На выполнение краевой диагностической работы по математике дается 90 минут. Работа состоит из двух частей, включающих в себя 12 заданий.
Часть 1 содержит 12 заданий (задания 1–12) базового уровня сложности, проверяющих наличие практических математических знаний и умений.
Ответом к каждому из заданий 1–12 является целое число или конечная десятичная дробь.
Бланк ответов заполняется яркими чёрными чернилами. Допускается использование гелиевой, капиллярной или перьевой ручки.
При выполнении заданий Вы можете пользоваться черновиком. Обращаем Ваше внимание, что записи в черновике не будут учитываться при оценивании работы.
Желаем успеха!
Часть 1
| Ответом на задания 1–12 должно быть целое число или конечная десятичная дробь. Ответ следует записать в бланк ответов № 1 справа от номера выполняемого задания, начиная с первой клеточки. Каждую цифру, знак минус и запятую пишите в отдельной клеточке в соответствии с приведёнными в бланке образцами. Единицы измерений писать не нужно. Если ответом является последовательность цифр, то запишите эту последовательность в бланк ответов № 1 без пробелов, запятых и других дополнительных символов. |
1. Мощность постоянного тока (в ваттах) вычисляется по формуле P = I2R, где I — сила тока (в амперах), R — сопротивление (в омах). Пользуясь этой формулой, найдите сопротивление R (в омах), если мощность составляет 224 Вт, а сила тока равна 4 А.
Ответ:______________________
2. На рисунке показано изменение температуры воздуха на протяжении трёх суток. По горизонтали указывается дата и время суток, по вертикали – значение температуры в градусах Цельсия. Определите по рисунку наименьшую температуру воздуха 27 апреля. Ответ дайте в градусах Цельсия.
Ответ:_______________________________
3. Турист подбирает экскурсии. Сведения об экскурсиях представлены
в таблице.
| Номер экскурсии | Посещаемые объекты | Стоимость (руб.) |
| 1 | Музей живописи, парк | 450 |
| 2 | Загородный дворец, крепость | 250 |
| 3 | Загородный дворец, музей живописи | 200 |
| 4 | Парк | 200 |
| 5 | Загородный дворец | 250 |
| 6 | Крепость | 150 |
Пользуясь таблицей, подберите набор экскурсий так, чтобы турист посетил четыре объекта: крепость, загородный дворец, парк и музей живописи,
а суммарная стоимость экскурсий не превышала 650 рублей. В ответе укажите какой-нибудь один набор номеров экскурсий без пробелов, запятых и других дополнительных символов.
Ответ:_______________________________
4. Найдите сумму координат вектора  , если А (2;4), В(8;6).
, если А (2;4), В(8;6).
Ответ: ________________________________
5. На железнодорожном вокзале 3 кассира. Каждый из них занят с клиентом с вероятностью 0,2 независимо от других кассиров. Найти вероятность того, что в случайный момент времени все три кассира заняты одновременно.
Ответ:__________________________
6. Решите уравнение: . В ответе укажите произведение корней.
Ответ:_________________________________
7. Найдите объём правильной шестиугольной пирамиды, если её апофема равна  и наклонена к плоскости основания под углом .
и наклонена к плоскости основания под углом .
Ответ:________________________________
8. На рисунке изображен график функции y=f(x) и отмечены точки −2, −1, 1, 4. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.
Ответ:__________________________________
9. Одна цилиндрическая кружка вдвое выше второй, зато вторая в два
раза шире. Найдите отношение площади боковой поверхности второй кружки к площади боковой поверхности первой.
Ответ:_________________________________
10. Найдите � �, если �
�, если � � -0,5 хЄ�
� -0,5 хЄ� �
�
Ответ:__________________________________
11. Первая труба пропускает на 14 литров воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает вторая труба, если резервуар объемом 528 литров она заполняет на 42 минуты быстрее, чем первая труба?
Ответ:_________________________________
12. Найдите наименьшее значение функции
Ответ:_________________________________
Краевая диагностическая работа по МАТЕМАТИКЕ
ВАРИАНТ № 4
На выполнение краевой диагностической работы по математике дается 90 минут. Работа состоит из двух частей, включающих в себя 12 заданий.
Часть 1 содержит 12 заданий (задания 1–12) базового уровня сложности, проверяющих наличие практических математических знаний и умений.
Ответом к каждому из заданий 1–12 является целое число или конечная десятичная дробь.
.
Бланк ответов заполняется яркими чёрными чернилами. Допускается использование гелиевой, капиллярной или перьевой ручки.
При выполнении заданий Вы можете пользоваться черновиком. Обращаем Ваше внимание, что записи в черновике не будут учитываться при оценивании работы.
Желаем успеха!
Часть 1
| Ответом на задания 1–12 должно быть целое число или конечная десятичная дробь. Ответ следует записать в бланк ответов № 1 справа от номера выполняемого задания, начиная с первой клеточки. Каждую цифру, знак минус и запятую пишите в отдельной клеточке в соответствии с приведёнными в бланке образцами. Единицы измерений писать не нужно. Если ответом является последовательность цифр, то запишите эту последовательность в бланк ответов № 1 без пробелов, запятых и других дополнительных символов. |
1. Длина биссектрисы lc, проведённой к стороне c треугольника со сторонами a, b и c, вычисляется по формуле Найдите длину биссектрисы lc, если a = 3, b = 9,
Ответ:______________________________
2. На рисунке жирными точками показано суточное количество осадков, выпадавших в городе N с 3 по 15 апреля 1900 года. По горизонтали указываются числа месяца, по вертикали – количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какого числа впервые выпало 4 миллиметра осадков.
Ответ:______________________________
3. В трёх салонах сотовой связи один и тот же телефон продаётся в кредит на разных условиях. Условия даны в таблице.
| Салон | Цена телефона (руб.) | Первоначальный взнос (в % от цены) | Срок кредита (мес.) | Сумма ежемесячного платежа (руб.) |
| Эпсилон | 15 400 | 25 | 12 | 1390 |
| Дельта | 16 200 | 5 | 6 | 3240 |
| Омикрон | 16 000 | 25 | 12 | 1350 |
Определите, в каком из салонов покупка обойдётся дешевле всего (с учётом переплаты). В ответе запишите эту сумму в рублях.
Ответ:________
4. Вектор  с началом в точке А (2;4) имеет координаты (6;2). Найдите абсциссу точки В.
с началом в точке А (2;4) имеет координаты (6;2). Найдите абсциссу точки В.
Ответ:________________________________
5. В ларьке на улице Счастья стоят два платежных автомата. Каждый из них может быть неисправен с вероятностью 0,1 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.
Ответ: _____________________________
6. Решите уравнение: .
Ответ: ____________________________
7. Диагональ основания BD правильной шестиугольной пирамиды SABCDEF равна , а высота равна . Найти объём пирамиды.
Ответ: ________________________
8. Материальная точка движется прямолинейно по закону x(t)=6t2−48t+17, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t=9 с.
Ответ:__________________________________
9. Однородный шар диаметром 3 см имеет массу 162 грамма. Чему равна масса шара, изготовленного из того же материала, с диаметром 2 см? Ответ дайте в граммах.
Ответ:_________________________________
10. Найдите � �если cosx=0,5 ч�
�если cosx=0,5 ч� �
�
Ответ:__________________________________
11. Один мастер может выполнить заказ за 6 часов, а другой — за 10 часов.
За сколько часов выполнят заказ оба мастера, работая вместе?
Ответ:_________________________________
12. Найдите наименьшее значение функции на отрезке [-33 ;-23]
Ответ:_________________________________
Тьюторская диагностическая работа по МАТЕМАТИКЕ
ВАРИАНТ № 5
На выполнение краевой диагностической работы по математике дается 90 минут. Работа состоит из двух частей, включающих в себя 12 заданий.
Часть 1 содержит 12 заданий (задания 1–12) базового уровня сложности, проверяющих наличие практических математических знаний и умений.
Ответом к каждому из заданий 1–12 является целое число или конечная десятичная дробь.
.
Бланк ответов заполняется яркими чёрными чернилами. Допускается использование гелиевой, капиллярной или перьевой ручки.
При выполнении заданий Вы можете пользоваться черновиком. Обращаем Ваше внимание, что записи в черновике не будут учитываться при оценивании работы.
Желаем успеха!
Часть 1
| Ответом на задания 1–12 должно быть целое число или конечная десятичная дробь. Ответ следует записать в бланк ответов № 1 справа от номера выполняемого задания, начиная с первой клеточки. Каждую цифру, знак минус и запятую пишите в отдельной клеточке в соответствии с приведёнными в бланке образцами. Единицы измерений писать не нужно. Если ответом является последовательность цифр, то запишите эту последовательность в бланк ответов № 1 без пробелов, запятых и других дополнительных символов. |
1. Среднее квадратическое трёх чисел  и
и  вычисляется по формуле . Найдите среднее квадратичное чисел
вычисляется по формуле . Найдите среднее квадратичное чисел 
 и
и  .
.
Ответ:________________________________
2. На рисунке жирными точками показана цена платины на момент закрытия биржевых торгов во все рабочие дни биржи с 13 по 31 октября 2009 года. По горизонтали указываются числа месяца, по вертикали – цена унции платины в долларах США. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку наибольшую цену платины на момент закрытия торгов в указанный период (в долларах США за унцию).
Ответ: ______________________________
3. Вася загружает на свой компьютер из Интернета файл размером 30 Мб за 29 секунд. Петя загружает файл размером 28 Мб за 26 секунд, а Миша загружает файл размером 32 Мб за 29 секунд. Сколько секунд будет загружаться файл размером 496 Мб на компьютер с наибольшей скоростью загрузки?
Ответ: _______________________________
4. Вектор  с концом в точке В (5;3) имеет координаты (3;1). Найдите ординату точки А.
с концом в точке В (5;3) имеет координаты (3;1). Найдите ординату точки А.
Ответ: _______________________________
5. За круглый стол на 51 стул в случайном порядке рассаживаются 49 мальчиков и 2 девочки. Найдите вероятность того, что обе девочки будут сидеть рядом.
Ответ: ____________________________
6. Решите уравнение:
Ответ:__________________________________
7. Диагональ основания правильной четырёхугольной пирамиды равна , а высота 15. Найдите объём пирамиды.
Ответ:__________________________________
8. Материальная точка движется прямолинейно по закону x(t)=t2−13t+23, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 3 м/с?
Ответ:__________________________________
9. Основание одной конусной воронки в вдвое больше основания второй, зато вторая конусная воронка выше первой в полтора раза. Найдите отношение объёма второй конусной воронки к объёму первой.
Ответ:_________________________________
10. Найдите значение выражения:� �если sinx=�
�если sinx=� �
�
Ответ:__________________________________
11. Бизнесмен получил в 2015 году прибыль в размере 20 000 рублей. Каждый следующий год его прибыль увеличивалась на 250% по сравнению с предыдущим годом. Сколько рублей заработал бизнесмен в 2018 году?
Ответ:_________________________________
12. Найдите наименьшее значение функции на отрезке
Ответ:_________________________________
Тьюторская диагностическая работа по МАТЕМАТИКЕ
ВАРИАНТ № 6
На выполнение краевой диагностической работы по математике дается 90 минут. Работа состоит из двух частей, включающих в себя 12 заданий.
Часть 1 содержит 12 заданий (задания 1–12) базового уровня сложности, проверяющих наличие практических математических знаний и умений.
Ответом к каждому из заданий 1–12 является целое число или конечная десятичная дробь.
Бланк ответов заполняется яркими чёрными чернилами. Допускается использование гелиевой, капиллярной или перьевой ручки.
При выполнении заданий Вы можете пользоваться черновиком. Обращаем Ваше внимание, что записи в черновике не будут учитываться при оценивании работы.
Желаем успеха!
Часть 1
| Ответом на задания 1–12 должно быть целое число или конечная десятичная дробь. Ответ следует записать в бланк ответов № 1 справа от номера выполняемого задания, начиная с первой клеточки. Каждую цифру, знак минус и запятую пишите в отдельной клеточке в соответствии с приведёнными в бланке образцами. Единицы измерений писать не нужно. Если ответом является последовательность цифр, то запишите эту последовательность в бланк ответов № 1 без пробелов, запятых и других дополнительных символов. |
1. Площадь прямоугольника вычисляется по формуле где d— диагональ, α — угол между диагоналями. Пользуясь этой формулой, найдите S , если d = 10 и
Ответ:________________________________
2. На диаграмме показана среднемесячная температура воздуха в Краснодаре за каждый месяц 2014 года. По горизонтали указываются месяцы, по вертикали – температура в градусах Цельсия. Определите по диаграмме наибольшую среднемесячную температуру в 2014 году. Ответ дайте в градусах Цельсия.
Ответ:________________________
3. По тарифному плану «Просто как день» компания сотовой связи каждый вечер снимает со счёта абонента 18 руб. Если на счету осталось меньше 18 руб., то на следующее утро номер блокируют до пополнения счёта. Сегодня утром у Лизы на счету было 800 руб. Сколько дней (включая сегодняшний) она сможет пользоваться телефоном, не пополняя счёт?
Ответ: _______________________________
4. Вектор  с началом в точке А (3;6) имеет координаты (9;3). Найдите абсциссу точки В.
с началом в точке А (3;6) имеет координаты (9;3). Найдите абсциссу точки В.
Ответ: _______________________________
5. Охотник Генри попадает в муху на стене с вероятностью 0,6 , если стреляет из пристрелянного ружья. Если Генри стреляет из непристрелянного ружья, то он попадает в муху с вероятностью 0,4. На столе лежит 12 ружей, из них 9 пристрелянные. Охотник Генри видит на стене муху, наудачу хватает первое попавшееся ружье и стреляет в муху. Найдите вероятность того, что Генри промахнется.
Ответ: ________________________________
6. Решите уравнение:
Ответ:__________________________________
7. Апофема боковой грани правильной четырёхугольной пирамиды равна и наклонена к плоскости основания под углом . Найдите объём пирамиды.
Ответ:_________________________________
8. Материальная точка движется прямолинейно по закону x(t)=� � t3−3t2−5t+3, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 2 м/с?
� t3−3t2−5t+3, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 2 м/с?
Ответ:__________________________________
9. Радиус основания одной конусной воронки в вдвое больше радиуса основания второй, но образующая второй конусной воронки больше первой в полтора раза. Найдите отношение площади боковой поверхности второй конусной воронки к площади боковой поверхности первой.
Ответ:_________________________________
10. Найдите значение выражения:1+tg2x,если cosx=� �
�
Ответ:__________________________________
11. Цена холодильника в магазине ежегодно уменьшается на одно и то же число процентов от предыдущей цены. Определите, на сколько процентов каждый год уменьшалась цена холодильника, если, выставленный на продажу за 20000 рублей, через два года был продан за 17672 рубля.
Ответ:_________________________________
12. Найти наибольшее значение функции на отрезке [-10; -1]
Ответ:_________________________________
Институт развития образования Краснодарского края
Сообщество тьюторов по математике Краснодарского Края







 . На диаграмме показано распределение выплавки некоторого металла в 10 странах мира (в тысячах тонн) за 2006 год. Среди представленных стран первое место по выплавке этого металла занимали США, десятое место – Казахстан. Какое место занимал Китай?
. На диаграмме показано распределение выплавки некоторого металла в 10 странах мира (в тысячах тонн) за 2006 год. Среди представленных стран первое место по выплавке этого металла занимали США, десятое место – Казахстан. Какое место занимал Китай? твет:_______________________________
твет:_______________________________ . На графике показан процесс разогрева двигателя легкового автомобиля при температуре окружающего воздуха 15 0 С. На оси абсцисс откладывается время в минутах, прошедшее от запуска двигателя, на оси ординат – температура двигателя Цельсия. Когда температура достигает определённого значения, включается вентилятор, охлаждающий двигатель, и температура начинает понижаться. Определите по графику, сколько минут прошло от момента запуска двигателя до включения вентилятора?
. На графике показан процесс разогрева двигателя легкового автомобиля при температуре окружающего воздуха 15 0 С. На оси абсцисс откладывается время в минутах, прошедшее от запуска двигателя, на оси ординат – температура двигателя Цельсия. Когда температура достигает определённого значения, включается вентилятор, охлаждающий двигатель, и температура начинает понижаться. Определите по графику, сколько минут прошло от момента запуска двигателя до включения вентилятора?