Понятие объема. Объём прямоугольного параллелепипеда.

Муниципальное казенное общеобразовательное учреждение

«Средняя общеобразовательная школа № 1» с. Дивное

Урок геометрии в 11 классе на тему

«Понятие объема.

Объём прямоугольного параллелепипеда.»

Выполнила

учитель математики

МКОУ СОЩ № 1

Титаренко Н.А.

13.02.2020

Тема урока «Понятие объема. Объём прямоугольного параллелепипеда.»

Цель урока: Выработка умений и навыков учащихся решать задачи на вычисление объёма прямоугольного параллелепипеда, применяя различные формулы для вычисления площади прямоугольников. Рассмотреть решение задач на вычисления объёма прямоугольного параллелепипеда при помощи многогранников. Провести срез знаний по данной теме.

Вид урока: урок закрепления и совершенствования знаний.

Оборудование: компьютер, проектор, слайды, чертёжные инструменты.

Структура урока:

1. Оргмомент.

2. Сообщение темы. Постановка целей

3. Решение задач

4. Физкульминутка

5. Математические развлечения

4. Самостоятельная работа.

5. Рефлексия.

6. Постановка домашнего задания.

Ход урока

1. Мотивация

Учитель объявляет тему и формулирует совместно с учениками цель урока. (СЛАЙД 1)

Вопросы учителя:

1. - что такое прямоугольный параллелепипед

(если его боковые ребра перпендикулярны к основанию, а основания представляют собой прямоугольники)

1. - сколько ребер имеет прямоугольный параллелепипед?

12

1. - сколько вершин имеет прямоугольный параллелепипед?

8

1. - как вычислить объем прямоугольного параллелепипеда (теорема)?

(объем параллелепипеда равен произведению трех его измерений)

1. - какое следствие из теоремы мы выучили (следствие 1)?

(объем параллелепипеда равен произведению площади основания на высоту)

Установите соответствие между параллелепипедом и формулой (СЛАЙД 2)

2. Решение задач

1.Объём куба равен 27дм³.Найдите площадь полной поверхности куба.

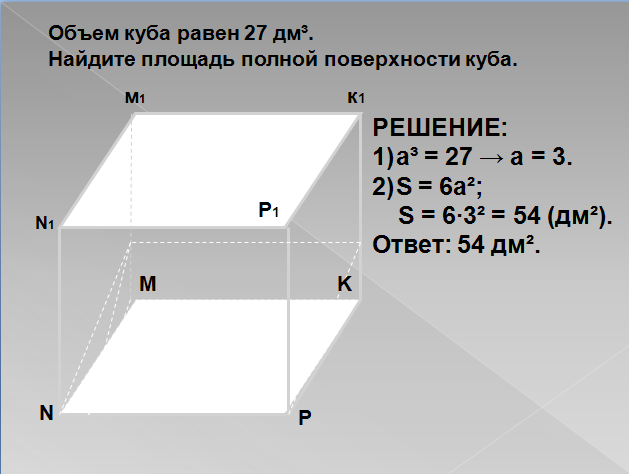( СЛАЙД 3)

Проверить по ключу. (СЛАЙД 4)

2.В прямоугольном параллелепипеде АВСDА₁В₁С₁D₁

АВ=8см; ВС=4см;СС₁=2см. Найдите ребро равновеликого куба. (СЛАЙД 5)

П роверить по ключу. (СЛАЙД 6)

3. В прямоугольном параллелепипеде АВСDА₁В₁С₁D₁, АВ=АD; АС=10см; АА₁=3√2см. Найдите объём. (СЛАЙД 7)

(Учитель совместно с учащимися анализирует условие и составляет план решений, а затем после самостоятельной деятельности учащихся проверит по ключу) (СЛАЙД 8)

4. АВСDА₁В₁С₁D₁ - прямоугольный параллелепипед АС∩ВД=0,∟СОB=150⁰, АА₁=5см; АС=10см

Н айдите объём прямоугольного параллелепипеда. (СЛАЙД 9)

(Учитель совместно с учащимися анализирует условие и составляет план решений, а затем после самостоятельной деятельности учащихся проверить по ключу) (СЛАЙД 10)

3 . Физкультминутка (СЛАЙД 11)

1. Сожмите кисть столько раз, сколько равна площадь прямоугольника со сторонами 3см, 2 см.

Ответ: 6 раз.

2. а=2см, в=1см

Вращение туловищем столько раз, сколько равен периметр прямоугольника.

Ответ: 6 раз

3. Присядьте столько раз, сколько будет равна площадь квадрата со стороной 1см.

Ответ: 1

4. «Математические развлечения»

I. Кто быстрее? (СЛАЙД 12)

А) Слова на букву «К»

1.Геометрическая фигура.

2.Произведение гипотенузы на косинус прилежащего угла.

3.Прямая, имеющая с окружностью только одну общую точку.

4.Отношение прилежащего катета к гипотенузе.

Б) Слова на букву «П» (СЛАЙД 13)

1)Наука, изучающая свойства фигур на плоскости.

2) Если 36см² = S кв, то 24 см - ?

3) Геометрическая фигура, все углы которой равны.

4) Отрезок, соединяющий основание наклонной и перпендикуляра.

5. Самостоятельная работа (по вариантам). (СЛАЙД 14)

I вариант

1) Объем прямоугольного параллелепипеда равен 96 см³, боковое ребро 8 см.

Чему равна площадь основания?

2) Диагонали куба 20 см. Найдите объём куба.

3) Основанием прямого параллелепипеда является квадрат со стороной 8√2 см. Диагональ боковой грани образует угол α с плоскостью основания. Найдите объём параллелепипеда.

II вариант

1) Объём прямоугольного параллелепипеда равен 100 см³, площадь основания 25 см². Найдите высоту параллелепипеда.

2) Диагональ куба равна 10 см. Найдите объём куба.

3) В прямоугольном параллелепипеде основанием является квадрат. Диагональ параллелепипеда равна 6 дм и образует угол £ с боковым ребром, имеющим с ней общее начало. Найдите объём прямоугольного параллелепипеда.

1. Рефлексия

1. Доволен ли ты тем, как прошел урок?

2. Было ли тебе интересно?

3. Сумел ли ты получить новые знания?

4. Был ли ты активен на уроке?

5. Ты с удовольствием будешь выполнять домашнее задание?

6. У читель был внимателен к тебе?

7. Сумел ли ты показать свои знания?

7. Итоги урока и домашнее задание. (СЛАЙД 15)

П. 74-75, № 657, № 658.

(СЛАЙД 16)