: Понятие о производной функции. Ее геометрический и физический смысл. Уравнение касательной к графику функции.

Алгебра и начала анализа – 11 класс

Тема урока: Понятие о производной функции. Ее геометрический и

физический смысл. Уравнение касательной к графику функции.

Цели урока: 1. Ввести понятие касательной к графику функции, производной и ее

геометрического и механического смысла.

2. Развитие познавательной деятельности учащихся, расширение

кругозора на основе межпредметных связей, развитие умений

слушать и слышать.

3. Содействовать воспитанию интереса и уважения к изучаемому

предмету, воспитание дружбы и взаимопомощи.

Тип урока: лекция.

Оборудование: учебник, тетрадь, ручка, карандаш, линейка.

Наглядность: справочный материал, карточки.

Ход урока.

I. Организационный момент.

1. Проверить готовность к уроку.

2. Сообщить тему урока, сформулировать цели и план урока.

3. Работа с тестами у доски. 10 класс, май. Задание А6.

Указать множество значений показательной функции.

II. Проверка домашнего задания. 1). № 180(а; в), № 181, № 186(а; б), № 187(б).

2). Работа над ошибками.

3). Карточки.

4). Устный опрос:

1. Сформировать понятие «приращение аргумента» и «приращение функции».

2. Сформировать понятие углового коэффициента прямой у = k x + b.

3. Сформировать понятие секущей к графику функции f.

4. Сформировать понятие углового коэффициента секущей, проходящей через точк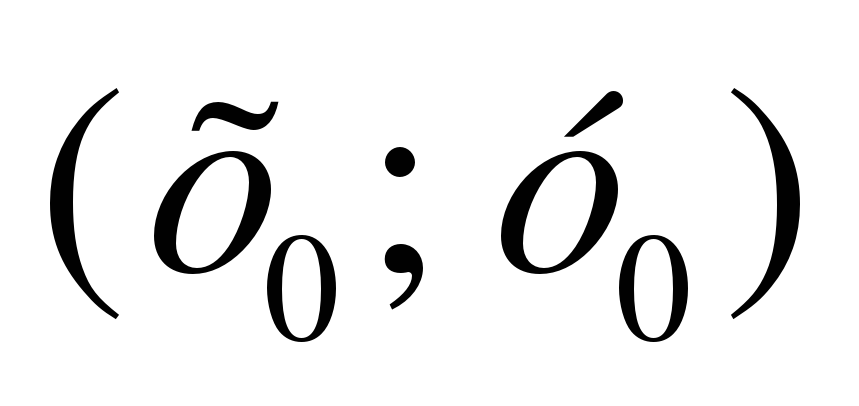и

и .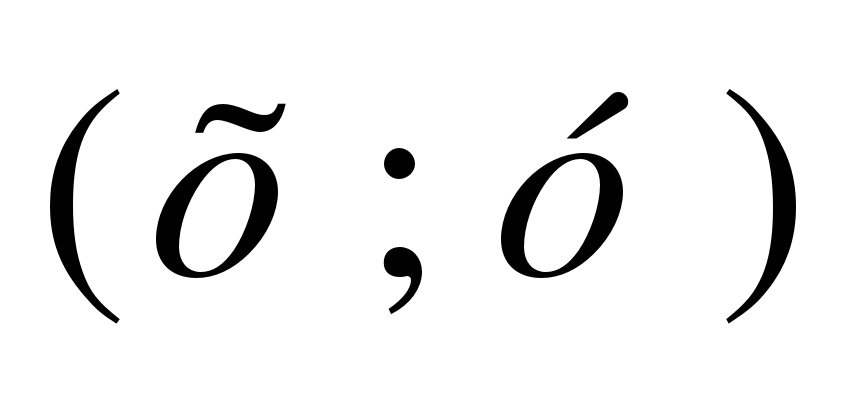

5. Выразить угловой коэффициент секущей через приращения ∆ х и ∆ у.

6. Средняя скорость, как отношение приращений ∆ f к ∆ х.

III. Изучение нового материала.

Вопросы лекции:

1. Понятие о касательной.

2. Определение производной.

3. Обозначение производной.

4. Понятие о дифференцируемой функции.

5. Понятие о дифференцировании.

6. Геометрический смысл производной.

7. Понятие об угловом коэффициенте касательной.

8. Формула углового коэффициента касательной.

9. Уравнение касательной к графику функции y= f ( x)

в заданной точке .

10. Формула Лагранжа о существовании касательной l к

графику функции f.

11. Механический смысл производной.

12. Второй физический смысл производной.

13. Понятие о производной второго порядка.

14. Формулы дифференцирования.

15. Работа с учебником.

Ход лекции.

1. Понятие о касательной. Касательной к кривой в данной точке М называется

предельное положение секущей MN, когда точка N приближается вдоль кривой к

точке М. Проходящую через точку 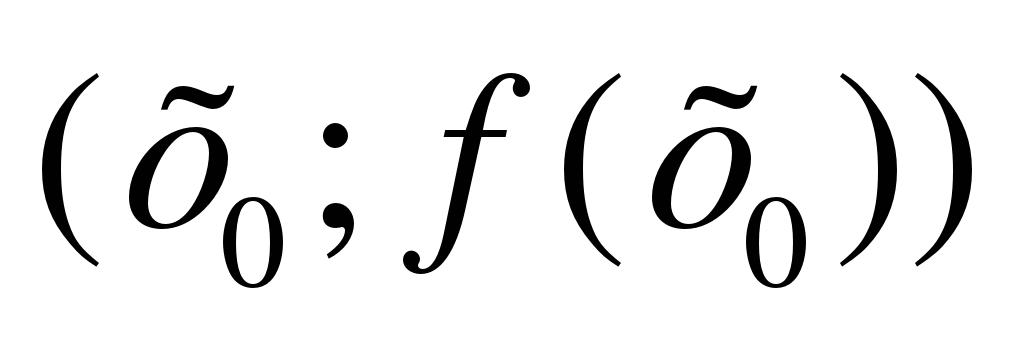прямую, с отрезком которой

практически сливается график функции f при значениях х, близких к ,

называют касательной к графику функции f в точке .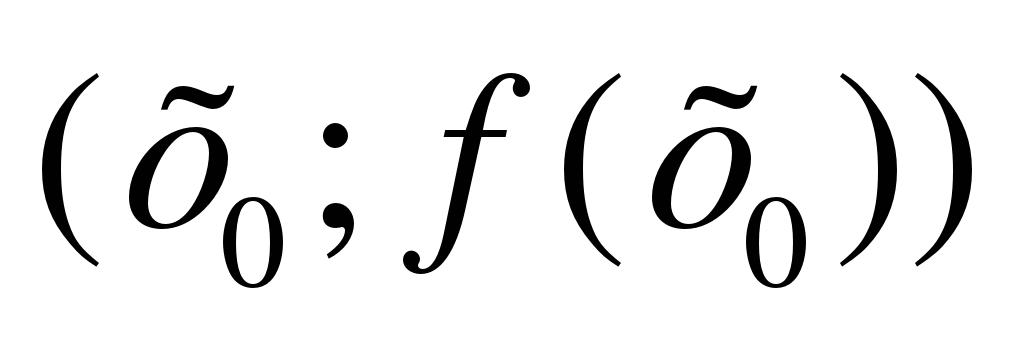

2. Определение производной. Производной функции f в точке называется число, к

которому стремится разностное отношение 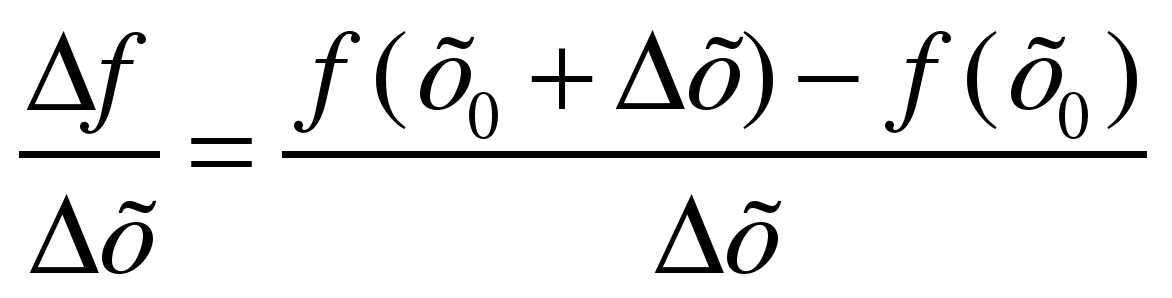при ,

стремящемуся к нулю, т.е.

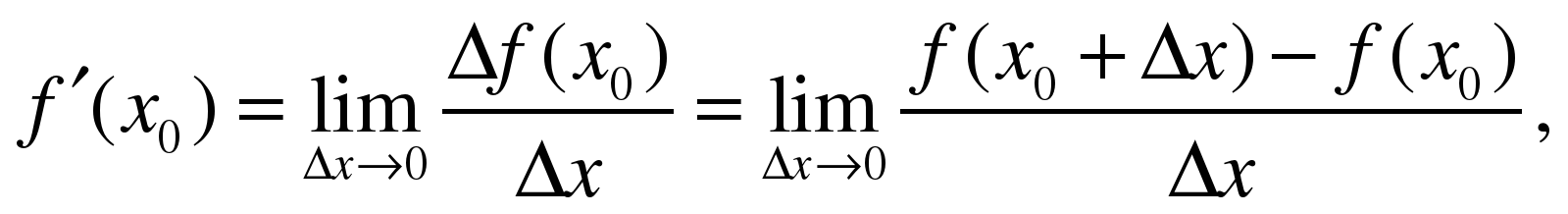где

3. Производная функции f в точке обозначается f ′().

4. Функцию, имеющую производную в точке , называют дифференцируемой в

этой точке.

5. Нахождение производной данной функции f называется дифференцированием.

6. Геометрический смысл производной: угловой коэффициент касательной к

графику функции равен значению производной этой функции в точке касания,

т. е. k = f ′().

7. Когда точка N приближается вдоль кривой к точке М, секущая МN стремится к

касательной, причем угол α стремится к углу φ между касательной и

положительным направлением оси Ох. В соответствии с определением

касательной получаем, что угловой коэффициент

касательной k = tg φ= 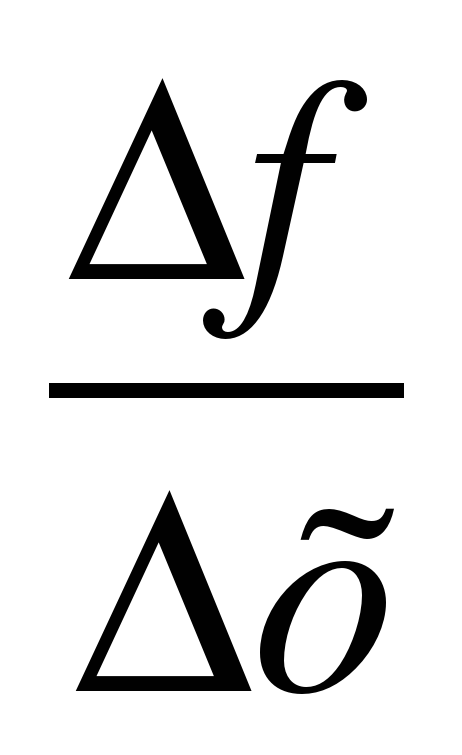= f ′().

8. Итак, k = tg φ= f ′().

9. Уравнение касательной к графику функции y= f ( x) в заданной точке :

f ′().

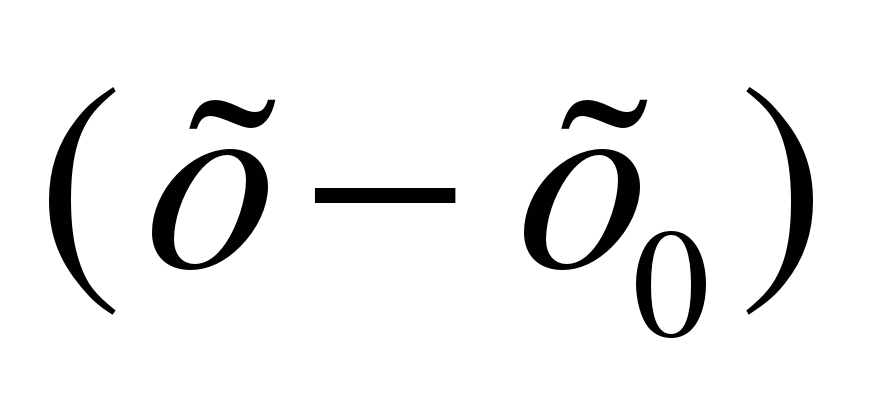10. Формула Лагранжа о существовании касательной l к графику функции f в точке с абсциссой c из интервала (a;b), параллельная секущей, проходящей через точки A(a; f (a)), B(b; f( b)). Прямая l, параллельная секущей, имеет с графиком функции f общую точку c из интервала (a;b). Тогда f ′( c )= tg α, где α – угол между прямой l и осью абсцисс. Но l ‌‌‌‌‌‌‌‌‌‌‍׀׀ AB, поэтому угол α равен углу наклона секущей AB, т. е. f ′( c ) = tg α =

Итак, если функция дифференцируема, то на интервале (a;b) найдется такая точка

c (a; b), что

f ′( c ) =

11. Точка движется прямолинейно по закону s = s(t), где s – перемещение точки за

время t. Механический смысл производной: мгновенная скорость точки в

данный момент времени равна значению производной от закона движения

v(t) = s′(t).

12. Второй физический смысл производной: ускорение точки в данный момент

времени равно значению второй производной от закона движения

a(t) = v′(t) = ( s′(t)′).

13. Производную от производной f ′( c ) мы будем называть производной второго

порядка или второй производной и обозначать f ′′( х ). Значит, a(t) = s′′(t).

14. Формулы дифференцирования:

с′ = 0, х′ = 1, (х ²)′ = 2х, (х³)′ = 3х², ( )′ = ,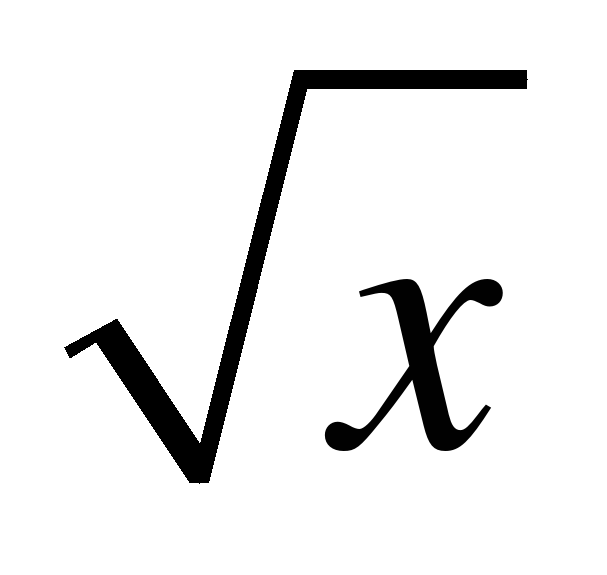

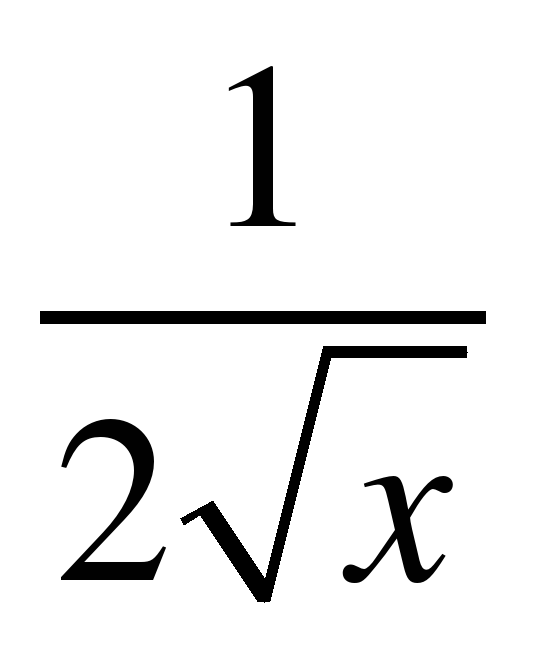15. Работа с учебником. Примеры 1,2 учебника.

IV. Решение упражнений. Задания по уровням.

Слабые дети решают задачи № 1, 3, 5. 6.

Сильные дети решают задачи № 1 – 7.

Задача № 1. Найти среднюю скорость изменения функции у = 3х² – 6

при изменении х от = 3 до = 3,5.

Решение. 1). Найдем приращение аргумента: ∆х = – = 3,5 – 3 = 0,5;

2). Вычислим приращение функции: ∆у = – = 3² – 6 – 3² + 6 = = 3(² – ²) = 9,75.

3). Найдем среднюю скорость изменения функции: ∆у/∆х =9,75/0,5 = 19, 5.

Ответ: 19,5.

Задача № 2. Прямолинейное движение точки задано уравнением s = 3t² – 2t + 5, где t

дано в секундах, а s – в метрах. Найти скорость движения точки

в момент t = 5с.

Решение. 1). Найдем среднюю скорость движения точки:

∆s = s( t + ∆t) – s(t) = 3(t + ∆t)² – 2(t + ∆t) + 5 – 3t² + 2t – 5 = 6t∆t + 3(∆t)² – 2∆t.

2). Найдем истинную скорость движения точки в момент времени t:

3). Найдем скорость движения точки в момент времени t = 5c:

v = 6t – 2 = 6·5 – 2 = 28 м/с.

Ответ: 28 м/с.

Задача № 3 . Материальная точка движется по закону х(t) = ⅓ t³ – ½ t² + 2. Выведите формулу для вычисления скорости в любой момент времени и найдите скорость в момент t = 5c. (Путь в метрах.)

Решение. 1). Найдем производную: v(t) = x′ (t) = (⅓ t³ – ½ t² + 2)′ = t² – t.

2). Найдем скорость в момент t = 5c: v(5) = 5² – 5 = 25 – 5 =20(м/с).

Ответ: v =20 м/с.

Задача №4. Пользуясь определением, найдите производную функции:

а) f(x) = х – 2. б) f (x) = 3x². в)

Решение. 1). Найдем приращение функции в точке х:

∆ f = f(x + ∆x) – f(x) = (x + ∆x) – 2 – ( x – 2) = x + ∆x – 2 – x + 2 = ∆x. 2). Найдем отношение приращения функции к приращению аргумента:

3). Найдем предел отношения приращения функции к приращению аргумента, то

есть производную в точке х:

Ответ:

Задача № 5. Найти угловой коэффициент касательной, проведенной к параболе у = 2х² в точке, абсцисса которой равна 1.

Решение. 1). Найдем производную: f ′(x) = (2x²)′ = 2 · 2x = 4x.

2). k = f ′(1) = 4·1 = 4.

Ответ: k = 4.

Задача № 6. Составить уравнение касательной к графику функции у = х² – 2х в точке с абсциссой = 3.

Решение. Уравнение касательной: f ′().

1) f (3) = 3² – 2·3 = 3.

2) f ′(х) = (х² – 2х)′ = 2х – 2.

3) f ′(3) = 2·3 – 2 = 4.

4) у = 3 + 4(х – 3) = 3+ 4х – 12 = 4х – 9.

у = 4х – 9 – уравнение касательной.

Ответ: у = 4х – 9.

Задача № 7. Найти координаты точки, в которой касательная к параболе

у = х² – х – 12 образует с осью Ох угол 45˚.

Решение. 1). tg α = у′(х) = (х² – х – 12)′ = 2х – 1.

2). Так как α = 45˚, то tg45˚ = 2х – 1,

1 = 2х – 1,

х = 1.

3) у(1) = 1 – 1 – 12 = – 12. М(1;12) – искомая точка.

Ответ: М(1;12).

V. Итоги урока. Итак, в ходе сегодняшнего урока мы рассмотрели понятия, как

производная, ее геометрический и физический смысл

касательная к графику функции. Решили задачи с применением

теоретического материала по указанной теме урока.

Объявление оценок.

VI. Домашнее задание: п. 13, п. 19, № 190, № 191 а, № 193 а, б,

№ 195 а, б, № 196 а, б, №253 а, б.

№191 а). f(х) = 2 х², = 1, ∆х = 0,5; 0,1; 0,001. Найти .

Решение. 1) ∆ f = f( + ∆x) – f() = 2( + ∆x)² – 2² = 2² + 4 ∆х + 2 ∆х² –

2² = 2 ∆х² + 4 ∆х

2)

3) при ∆х = 0,5 и = 1 имеем 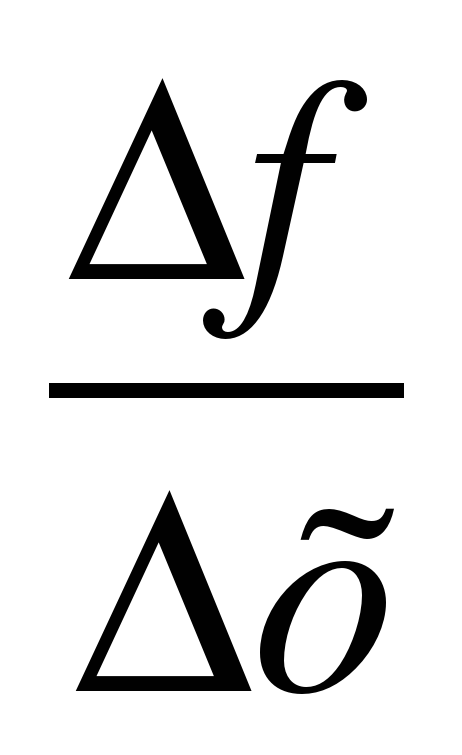= 2·0,5 +4·1 = 1+ 4 = 5;

при ∆х = 0,1 и = 1 имеем 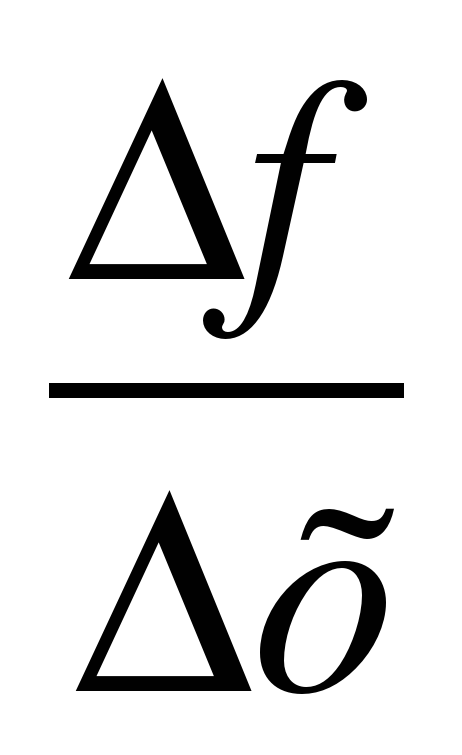= 2·0,1 +4·1 = 0,1+ 4 = 4,1;

при ∆х = 0,001 и = 1 имеем 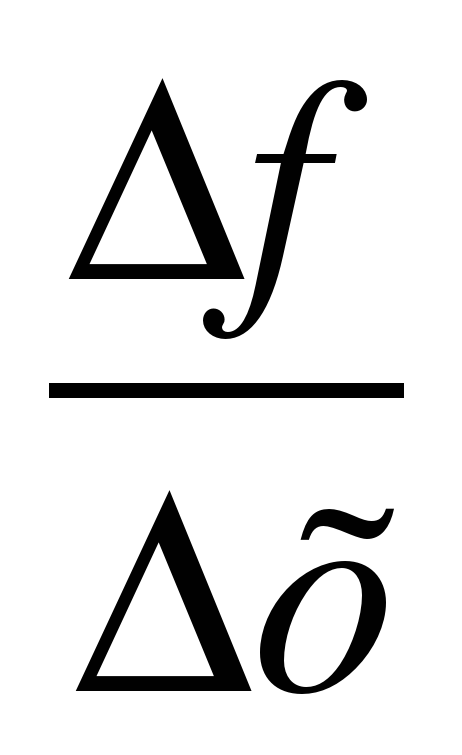= 2·0,001 +4·1 = 0,001+ 4 = 4,001.

Ответ: 5; 4,1; 4,001.

№ 193 а). f(x) = x³, = 2; = – 1, 5.

Решение. 1) f ′(x) = (x³)′ = 3x².

2) при = 2 имеем f ′(2) = 3·2² = 12;

3) при = – 1, 5 имеем f ′(– 1, 5) = 3·(– 1, 5)² = 3·2,25 = 6,75.

№ 193 б). f(x) = 4 – 2х, = 0,5; = – 3.

Решение. 1) f ′(x) = (4 – 2х)′ = 0 – 2·1 = – 2.

2) при = 0,5 имеем f ′(0,5) = 0,5;

3) при = – 3 имеем f ′(– 3) = – 3.

Ответ: а) 12; 6,75; б) 0,5; – 3.

№ 195 а). Составить уравнение касательной к графику функции у = х² в точке с абсциссой = –1.

Решение. Уравнение касательной: f ′().

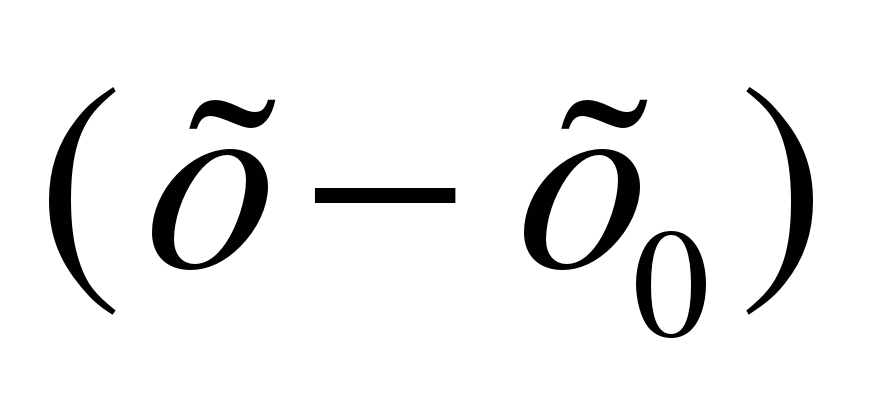1) f (–1) = (–1)² = 1.

2) f ′(х) = (х²)′ = 2х.

3) f ′(–1) = 2·(–1) = –2.

4) у = 1 –2(х + 1) = 1 –2х – 2 = –2х – 1.

у = –2х – 1 – уравнение касательной.

Ответ: у = –2х – 1.

Дополнительное задание:

Найдите все значения х, при каждом из которых выражения

и принимают равные значения.

Решение:

Так как cos 3 х 0, то

Ответ: