Построение сечений многогранников. 10 класс.
Правила построения сечений многогранников:
1) проводим прямые через точки, лежащие в одной плоскости;
2) ищем прямые пересечения плоскости сечения с гранями многогранника, для этого
а) ищем точки пересечения прямой принадлежащей плоскости сечения с прямой, принадлежащей одной из граней (лежащие в одной плоскости);
б) параллельные грани плоскость сечения пересекает по параллельным прямым.
Примеры построения сечений:
Пример 1.
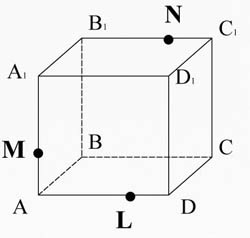
Рассмотрим прямоугольный параллелепипед ABCDA1B1C1D1. Построим сечение, проходящее через точки M, N, L.
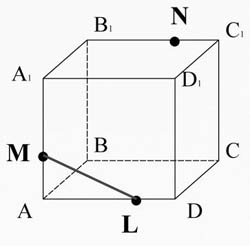
Соединим точки M и L, лежащие в плоскости AA1D1D.
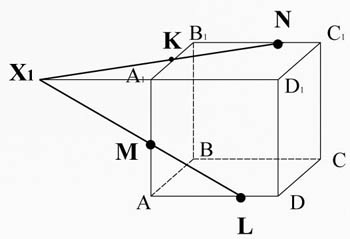
Пересечем прямую ML ( принадлежащую сечению) с ребром A1D1, они лежат в одной плоскости AA1D1D. Получим точку X1.

Точка X1 лежит на ребре A1D1, а значит и плоскости A1B1C1D1, соединим ее сточкой N, лежащей в этой же плоскости.
X1 N пересекается с ребром A1B1 в точке К.
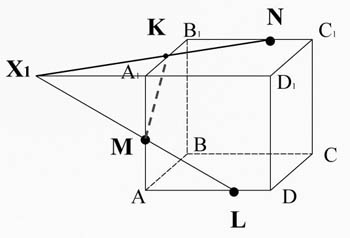
Соединим точки K и M, лежащие в одной плоскости AA1B1B.
Найдем прямую пересечения плоскости сечения с плоскостью DD1C1C:
пересечем прямую ML (принадлежащую сечению) с ребром DD1, они лежат в одной плоскости AA1D1D, получим точку X2;
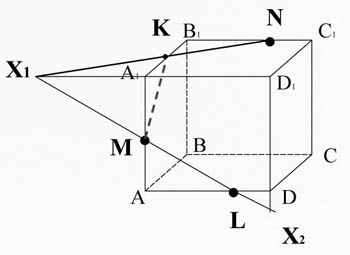
пересечем прямую KN (принадлежащую сечению) с ребром D1C1, они лежат в одной плоскости A1B1C1D1, получим точку X3;

Точки X2 и X3 лежат в плоскости DD1C1C. Проведем прямую X2 X3 , которая пересечет ребро C1C в точке T, а ребро DC в точке P. И соединим точки L и P, лежащие в плоскости ABCD.
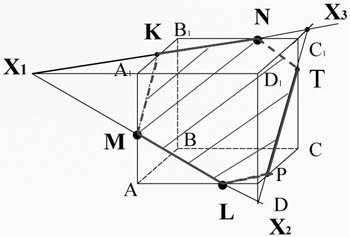
MKNTPL - искомое сечение.
Пример 2.
Рассмотрим ту же самую задачу на построение сечения, но воспользуемся свойством параллельных плоскостей. Это облегчит нам построение сечения.
 .
.
Соединим точки M и L, лежащие в плоскости AA1D1D.
 .
.
Через точку N, проведем прямую NT параллельную прямой ML. Прямые NT и ML лежат в параллельных плоскостях по свойству параллелепипеда.
 .
.
Пересечем прямую ML ( принадлежащую сечению) с ребром A1D1, они лежат в одной плоскости AA1D1D. Получим точку X1.
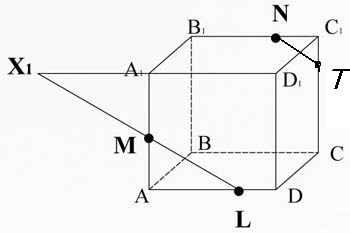 .
.
Точка X1 лежит на ребре A1D1, а значит и плоскости A1B1C1D1, соединим ее сточкой N, лежащей в этой же плоскости.
X1 N пересекается с ребром A1B1 в точке К.
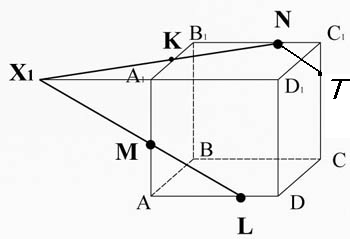 .
.
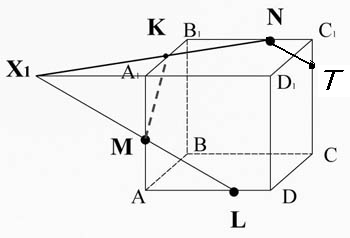
Соединим точки K и M, лежащие в одной плоскости AA1B1B.
 .
.
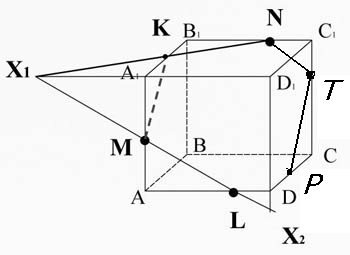
Проведем прямую TP через точку T, параллельно прямой KM ( они лежат в параллельных плоскостях).
 .
.
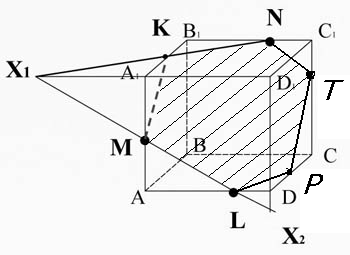
Соединим точки P и L ( они лежат в одной плоскости).
 .
.
MKNTPL - искомое сечение.
Методы построения сечений
Метод следов
В общем случае плоскость сечения имеет общую прямую с плоскостью каждой грани многогранника. Прямую, по которой секущая плоскость пересекает какую-либо грань, называют следом секущей плоскости.
Метод внутреннего проектирования
Этот метод удобен при построении сечений в тех случаях, когда почему-либо неудобно находить след секущей плоскости, например, след получается очень далеко от заданной фигуры.
Комбинированный метод
При построении этим методом на каких-то этапах применяются приёмы, изложенные в методе следов или методе внутреннего проектирования, а на других этапах применяются теоремы, изученные в разделе «Параллельность прямых и плоскостей».
Метод следов
Суть метода заключается в построении вспомогательной прямой, являющейся изображением линии пересечения секущей плоскости с плоскостью какой-либо грани фигуры F. Удобнее всего строить изображение линии пересечения секущей плоскости с плоскостью нижнего основания. Эту линию называют следом секущей плоскости. Используя след, легко построить изображения точек секущей плоскости, находящихся на боковых ребрах или гранях фигуры F.
Пусть М, N, К - точки секущей плоскости, М1, N1, К1 - их проекции на плоскость основания. При этом для призм и цилиндров ММ1 || NN1, NN1 || КК1, для конусов и пирамид ММ1∩ NN1 ∩ КК1= S (S- вершина). Удобнее обозначать вершины нижнего основания через А1, В1, С1,... верхнего основания - А, В, С,.... Кратко суть метода следов можно записать следующим образом.
1. МN ∩ М1N1=X
2. МК ∩ М1К1=У
3. ХУ= S - след секущей плоскости
4. A1M1 ∩ S = A0 возможно
5. АоМ ∩ А1А == А
6. Пункты 4-5 повторить для вершин В1, С1,... нижнего основания фигуры F;
7. - искомое сечение.
Строить сечение фигуры F секущей плоскостью α методом следов удобно в тех случаях, когда секущая плоскость задана тремя точками, ей принадлежащими, или прямой и не принадлежащей ей точкой, или двумя пересекающимися прямыми, или двумя параллельными прямыми. Во всех случаях легко взять три точки М, N, К, принадлежащие плоскости α, и решение проводить по указанной схеме.
Задача 1. Постройте сечение призмы A1B1C1D1ABCD плоскостью, проходящей через три точки M, N, K. Рассмотрите все случаи расположения точек M, N, K на поверхности призмы (рис. 13).
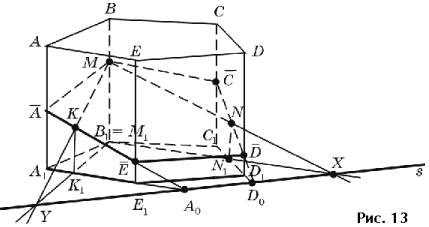
Рассмотрим случай: 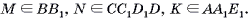 В данном случае очевидно, что M1 = B1.
В данном случае очевидно, что M1 = B1.
Построение.

2. 
3. XY = s – след секущей плоскости.
4. 
5. 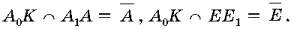
6. 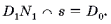
7. 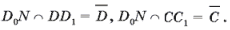
8. 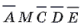 – искомое сечение.
– искомое сечение.
Задача 2. Постройте сечение пирамиды SABCDE плоскостью, проходящей через точку  и прямую l, лежащую в грани SED (рис. 14).
и прямую l, лежащую в грани SED (рис. 14).
Построение.
1.
2.
3. – след секущей плоскости.
4.
5.
6. – искомое сечение.
Задача 3. Точки P, Q и R взяты на поверхности параллепипеда ABCDA1B1C1D1 следующим образом: точка P лежит в грани CC1D1D, точка Q - в грани AA1D1D, точка R на прямой BB1. Построить сечение параллелепипеда плоскостью (PQR).
Метод внутреннего проектирования.
Задача 4. Точки P, Q и R взяты на поверхности параллепипеда ABCDA1B1C1D1 следующим образом: точка P лежит на грани CC1D1D, точка Q - на ребре B1C1, а точка R - на ребре AA1. Построить сечение параллелепипеда плоскостью (PQR).
Комбинированный метод.
Задача 5. На рёбрах A1B1 и DD1 параллелепипеда ABCDA1B1C1D1 взяты соответственно точки P и S, а в гранях DD1C1C и AA1D1D соответственно точки Q и R. Построить сечение параллелепипеда плоскостью, проходящей через точку S параллельно плоскости PQR.















 .
. .
. .
. .
. .
. .
.




















