Дата проведения:
Тема «Поворот точки вокруг начала координат»
Тип урока: освоение нового материала
Цели урока:
Обучающие:
- Освоить и закрепить основные понятия базового уровня
- Обеспечить условия для усвоения новых знаний
Развивающие:
- Создать условия для развития математически грамотной речи, логического мышления, сознательного восприятия учебного материала.
Воспитательные:
- Продолжить воспитание познавательной активности, культуры общения, культуры диалога;
Формы работы: фронтальная, групповая, индивидуальная
- Оснащение урока:
- Содержание урока: Учебник « Алгебра и начала анализа», А.Н.Колмогоров
2-ой урок по теме «Тригонометрические формулы
Ход урока.
1. Организационный
1.Сообщает тему урока
2. Объясняет цели, задачи и план урока., а так же систему оценивания работы учеников (мотивация)
.
2. Новая тема
1.Найдите координаты точек А, В, С и D, лежащих на единичной окружности (рис. 1)

Рисунок 1 – единичная окружность
Определите координаты точек А;В;С;D;
Ответ: А(1; 0); В(0; 1); С(-1; 0); D(0; -1)
Сегодня на уроке мы узнаем, как по-другому называются абсцисса и ордината точки, лежащей на единичной окружности.
1.Рассмотрим окружность радиуса, равного 1 единичному отрезку, в прямоугольной системе координат хОу с центром в начале координат. Такую окружность называют
единичной или тригонометрической.

Рисунок 2 – точка Р на единичной окружности Точка Р (1; 0) при повороте вокруг начала координат на угол  переместилась в точку Рₐ. Определим её координаты. (рис. 2).
переместилась в точку Рₐ. Определим её координаты. (рис. 2).
Определения. Синусом угла  называется ордината точки, полученной поворотом точки (1; 0) вокруг начала координат на угол
называется ордината точки, полученной поворотом точки (1; 0) вокруг начала координат на угол .
.
Обозначается
Косинусом угла называется абсцисса точки, полученной поворотом точки (1; 0) вокруг начала координат на угол
называется абсцисса точки, полученной поворотом точки (1; 0) вокруг начала координат на угол  .Обозначается
.Обозначается  Угол
Угол  может выражаться и в градусах и в радианах.
может выражаться и в градусах и в радианах.
3.Закрепление
Пример 1. Точка А(1; 0) при повороте на угол 90 (рис. 1)
(рис. 1)
Ордината точки В равна 1, значит  или
или
Абсцисса точки В равна 0, значит 
Пример 2. Точка А(1; 0) при повороте на угол  переместилась в точку
переместилась в точку ( рис. 1)
( рис. 1)
Найдите  и
и 
Ответ:  = 0;
= 0; 
Пример 3. Точка А(1; 0) при повороте на угол  переместилась в точку
переместилась в точку  (рис. 1)
(рис. 1)
Найдите  и
и 
Ответ:  =
= 1
1 = 0.
= 0.
Рассмотрим ещё два понятия.
Определение. Тангенсом угла  называется отношение синуса угла к его косинусу.
называется отношение синуса угла к его косинусу.
tg ,
, 
Пример 4. Найти tg 0. Вычислим по формуле tg  =
=  = 0.
= 0.
Определение. Котангенсом угла  называется отношение косинуса угла к его синусу.
называется отношение косинуса угла к его синусу.
сtg
4.Итог урока
Оценивание, Д/задание
Просмотр содержимого документа
«Поворот точки вокруг начала координат»»
Дата проведения:
Тема «Поворот точки вокруг начала координат»
Тип урока: освоение нового материала
Цели урока:
Обучающие:
Освоить и закрепить основные понятия базового уровня
Обеспечить условия для усвоения новых знаний
Развивающие:
Создать условия для развития математически грамотной речи, логического мышления, сознательного восприятия учебного материала.
Воспитательные:
Продолжить воспитание познавательной активности, культуры общения, культуры диалога;
Формы работы: фронтальная, групповая, индивидуальная
Оснащение урока:
Содержание урока: Учебник « Алгебра и начала анализа», А.Н.Колмогоров
2-ой урок по теме «Тригонометрические формулы
Ход урока.
1. Организационный
1.Сообщает тему урока
2. Объясняет цели, задачи и план урока., а так же систему оценивания работы учеников (мотивация)
.
2. Новая тема
1.Найдите координаты точек А, В, С и D, лежащих на единичной окружности (рис. 1)
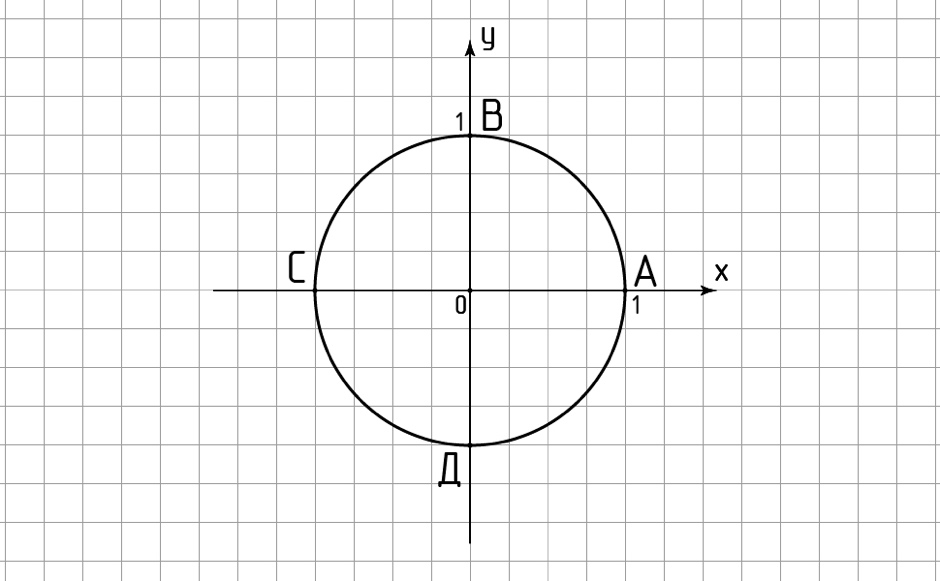
Рисунок 1 – единичная окружность
Определите координаты точек А;В;С;D;
Ответ: А(1; 0); В(0; 1); С(-1; 0); D(0; -1)
Сегодня на уроке мы узнаем, как по-другому называются абсцисса и ордината точки, лежащей на единичной окружности.
1.Рассмотрим окружность радиуса, равного 1 единичному отрезку, в прямоугольной системе координат хОу с центром в начале координат. Такую окружность называют
единичной или тригонометрической.
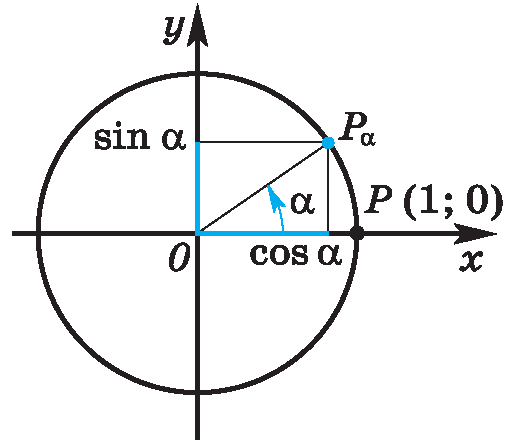
Рисунок 2 – точка Р на единичной окружности Точка Р (1; 0) при повороте вокруг начала координат на угол  переместилась в точку Рₐ. Определим её координаты. (рис. 2).
переместилась в точку Рₐ. Определим её координаты. (рис. 2).
Определения. Синусом угла  называется ордината точки, полученной поворотом точки (1; 0) вокруг начала координат на угол
называется ордината точки, полученной поворотом точки (1; 0) вокруг начала координат на угол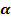 .
.
Обозначается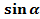
Косинусом угла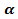 называется абсцисса точки, полученной поворотом точки (1; 0) вокруг начала координат на угол
называется абсцисса точки, полученной поворотом точки (1; 0) вокруг начала координат на угол 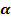 .Обозначается
.Обозначается  Угол
Угол 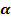 может выражаться и в градусах и в радианах.
может выражаться и в градусах и в радианах.
3.Закрепление
Пример 1. Точка А(1; 0) при повороте на угол 90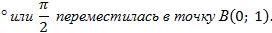 (рис. 1)
(рис. 1)
Ордината точки В равна 1, значит 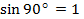 или
или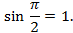
Абсцисса точки В равна 0, значит 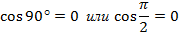
Пример 2. Точка А(1; 0) при повороте на угол 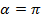 переместилась в точку
переместилась в точку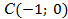 ( рис. 1)
( рис. 1)
Найдите 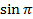 и
и 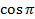
Ответ:  = 0;
= 0; 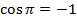
Пример 3. Точка А(1; 0) при повороте на угол 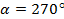 переместилась в точку
переместилась в точку 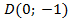 (рис. 1)
(рис. 1)
Найдите 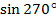 и
и 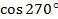
Ответ: 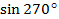 =
=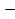 1
1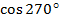 = 0.
= 0.
Рассмотрим ещё два понятия.
Определение. Тангенсом угла 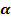 называется отношение синуса угла к его косинусу.
называется отношение синуса угла к его косинусу.
tg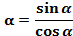 ,
, 
Пример 4. Найти tg 0. Вычислим по формуле tg 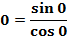 =
= 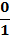 = 0.
= 0.
Определение. Котангенсом угла 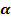 называется отношение косинуса угла к его синусу.
называется отношение косинуса угла к его синусу.
сtg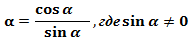
4.Итог урока
Оценивание, Д/задание








 переместилась в точку Рₐ. Определим её координаты. (рис. 2).
переместилась в точку Рₐ. Определим её координаты. (рис. 2). называется ордината точки, полученной поворотом точки (1; 0) вокруг начала координат на угол
называется ордината точки, полученной поворотом точки (1; 0) вокруг начала координат на угол .
.
 называется абсцисса точки, полученной поворотом точки (1; 0) вокруг начала координат на угол
называется абсцисса точки, полученной поворотом точки (1; 0) вокруг начала координат на угол  .Обозначается
.Обозначается  Угол
Угол  может выражаться и в градусах и в радианах.
может выражаться и в градусах и в радианах. (рис. 1)
(рис. 1) или
или

 переместилась в точку
переместилась в точку ( рис. 1)
( рис. 1) и
и 
 = 0;
= 0; 
 переместилась в точку
переместилась в точку  (рис. 1)
(рис. 1) и
и 
 =
= 1
1 = 0.
= 0. называется отношение синуса угла к его косинусу.
называется отношение синуса угла к его косинусу. ,
, 
 =
=  = 0.
= 0. называется отношение косинуса угла к его синусу.
называется отношение косинуса угла к его синусу.












