Тригонометрические функции

Тригонометрические Функции

Поворот точки вокруг начала координат

0

1. Какая фигура называется углом ?

2. В чем измеряются углы?

3. Какие углы бывают, примеры их величин?

4. Какой угол принимают за угол в 1 0 ?

5 . Что такое угол в один радиан?

6 . Каково соотношение между радианом и градусом?

7 . Сколько радиан составляют 180 0 ?

Проверочная работа

180 0 = π

Вариант 2

Вариант 1

3

Ответы на проверочную работу

Оценка за проверочную работу:

7-8 верных ответов - оценка « 3 »

9-10 верных ответов – оценка « 4 »

11-12 верных ответов – оценка « 5 »

3

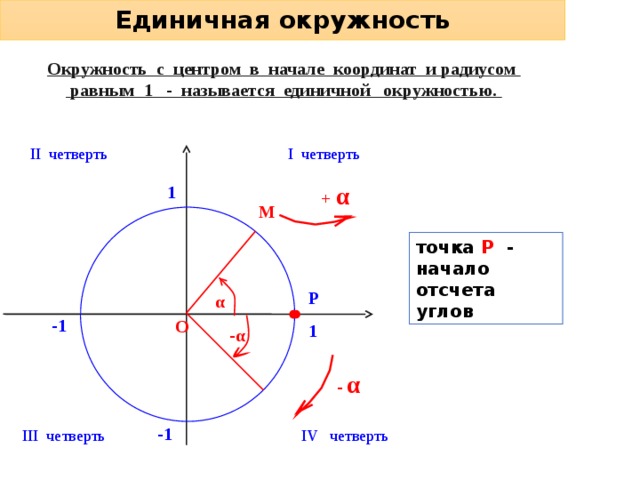
Единичная окружность

Окружность с центром в начале координат и радиусом

равным 1 - называется единичной окружностью.

II четверть

I четверть

+ α

1

М

точка Р - начало отсчета углов

α

Р

-1

О

1

-α

- α

-1

III четверть

IV четверть

3

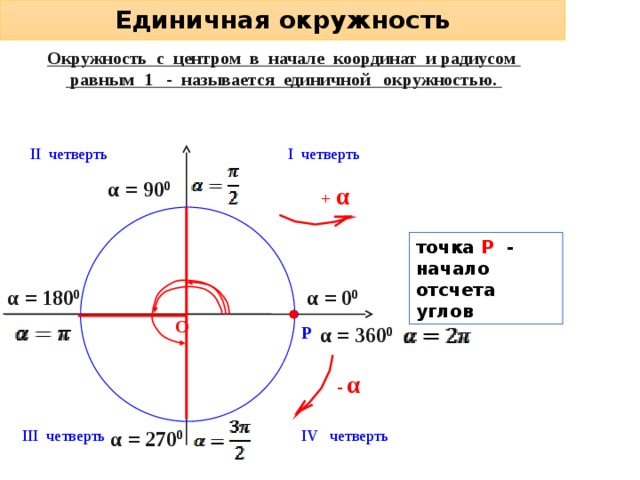
Единичная окружность

Окружность с центром в начале координат и радиусом

равным 1 - называется единичной окружностью.

II четверть

I четверть

α = 90 0

+ α

точка Р - начало отсчета углов

α = 180 0

α = 0 0

О

α = 360 0

Р

- α

α = 270 0

IV четверть

III четверть

3

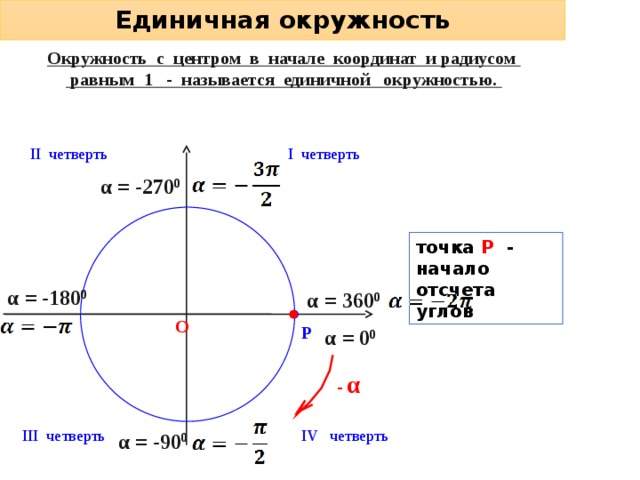
Единичная окружность

Окружность с центром в начале координат и радиусом

равным 1 - называется единичной окружностью.

II четверть

I четверть

α = - 270 0

точка Р - начало отсчета углов

α = - 180 0

α = 360 0

О

Р

α = 0 0

- α

IV четверть

III четверть

α = - 90 0

3

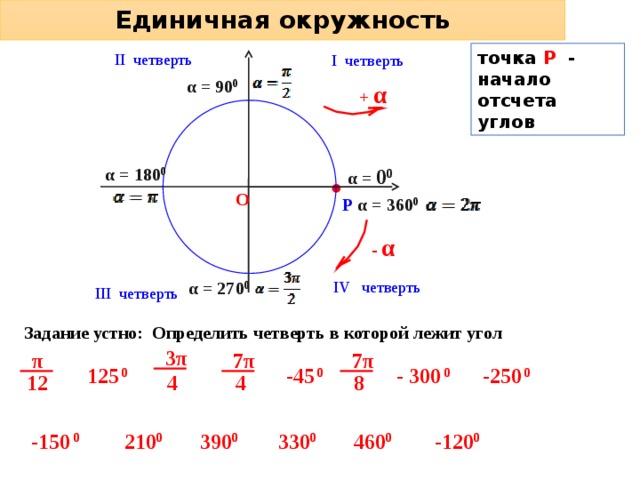
Единичная окружность

точка Р - начало отсчета углов

II четверть

I четверть

α = 90 0

+ α

α = 0 0

α = 180 0

О

Р

α = 360 0

- α

α = 270 0

IV четверть

III четверть

Задание устно: Определить четверть в которой лежит угол

3π

π

7π

7π

-250 0

- 300 0

125 0

-45 0

4

8

4

12

-150 0

210 0

330 0

390 0

460 0

-120 0

8