Просмотр содержимого документа
«Практическая работа № 1 "Сложение дробей с разными знаменателями"»
Практическая работа №1 «Сложение дробей с разными знаменателями»
Цель работы: Проверить умения слаживать дроби с разными знаменателями.
Теоретические сведения к практической работе
Чтобы найти сумму дробей 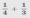 нужно выполнить следующие шаги:
нужно выполнить следующие шаги:
1. Привести дроби к наименьшему общему знаменателю НОК(4, 3) = 12, в результате получим: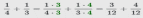 .
.
2. Сложить числители дробей, знаменатель остается неизменным: 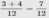 .
.
3. Сократить полученную дробь, в данном примере получили несократимую дробь 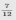 .
.

Пример: Сложить дроби 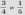 .
.
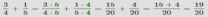 .
.
Чтобы проверить результат сложения дробей, можно воспользоваться калькулятором дробей.
Пример: Найти сумму дробей 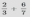 .
.
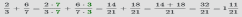 .
.
Основное свойство дроби:
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Сложение смешанных чисел:
Чтобы сложить смешанные числа, надо записать их в виде неправильных дробей, а затем сложить как обыкновенные дроби. Часто удобней вначале сложить целые части, а затем дробные части, избегаю преобразования в неправильную дробь.
Пример: Сложить смешанные числа 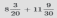
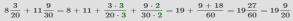
Сократим дробь 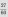 с помощью нахождения наибольшего общего делителя числителя и знаменателя и деления полученного числа на числитель и знаменатель, НОД(27,60)=3, получим
с помощью нахождения наибольшего общего делителя числителя и знаменателя и деления полученного числа на числитель и знаменатель, НОД(27,60)=3, получим 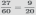 .
.
Пример: Найти сумму смешанных чисел 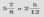
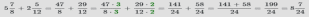 .
.
В результате сложения также получим смешанное число.
Сложение нескольких дробей
Пример: Сложить 3 дроби 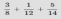
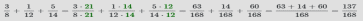 .
.
Сложение обыкновенных и десятичных дробей
Пример: Найти сумму 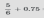
Для сложения десятичных и обыкновенных дробей нужно преобразовать их к одному формату. В данном примере преобразуем десятичную дробь 0.75 в обыкновенную дробь 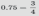 .
.
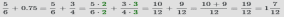 .
.
Задания для самостоятельного решения:
I вариант
Представить неправильные дроби в виде смешанных чисел:
а) 29 б) 17 в) 40 г) 15 д) 40
6 8 7 5 8
Записать смешанные числа в виде неправильной дроби:
а) 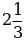 б)
б) 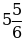 в)
в) 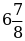 г)5 д)
г)5 д) 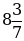
Выполнить сложение дробей:
а) 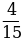 +
+ 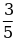 б)
б) 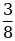 +
+ 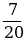 в)
в) 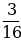 +
+ 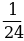 г)
г) 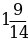 +
+ 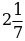 д)
д) 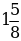 +
+ 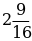
II вариант
Представить неправильные дроби в виде смешанных чисел:
а) 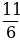 б)
б) 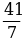 в)
в) 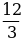 г)
г) 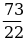 д)
д) 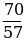
Записать смешанные числа в виде неправильной дроби:
а) 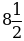 б)
б) 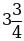 в)
в) 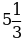 г)
г) 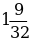 д) 3
д) 3
Выполнить сложение дробей:
а) 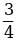 +
+ 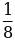 б)
б) 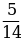 +
+ 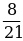 в)
в) 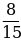 +
+ 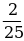 г)
г) 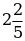 +
+ 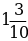 д)
д) 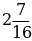 +
+ 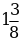
Контрольные вопросы:
1. Какие виды дробей вы знаете?
2. Как называется дробь с целой и дробной частью?
3. Основное свойство дроби.







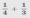 нужно выполнить следующие шаги:
нужно выполнить следующие шаги: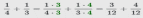 .
.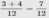 .
.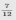 .
.
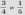 .
.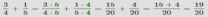 .
.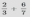 .
.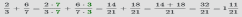 .
.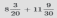
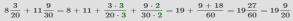
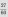 с помощью нахождения наибольшего общего делителя числителя и знаменателя и деления полученного числа на числитель и знаменатель, НОД(27,60)=3, получим
с помощью нахождения наибольшего общего делителя числителя и знаменателя и деления полученного числа на числитель и знаменатель, НОД(27,60)=3, получим 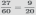 .
.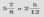
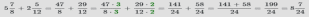 .
.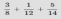
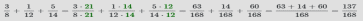 .
.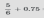
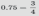 .
.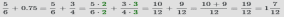 .
.









