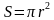Тишевская Лилия Сергеевна
МБОУСШ №7, г.Волгодонск
План-конспект урока.
Класс: 6 класс ( УМК Н.Я.Виленкин )
Тема урока: Длина окружности и площадь круга.
Тип урока: Комбинированный ( лабораторная работа и изучение нового материала).
Цель и задачи урока: Опытным путём получить приближенное значение числа  , самостоятельный вывод формулы длины окружности. Знакомство с формулой площади круга. Применение новых знаний в решении задач.
, самостоятельный вывод формулы длины окружности. Знакомство с формулой площади круга. Применение новых знаний в решении задач.
Результаты обучения:
Предметные: Вспомнить построение окружности и её элементов. Научиться отличать круг от окружности. Находить длину окружности расчетным и опытным путём. Находить площадь круга расчетным путём.
Метапредметные: Сформировать умение находить математические формулы и константы опытным путём.
Личностные: сформировать умение работать в коллективе, умение на практике разрешать проблемные ситуации, сформировать интерес к изучаемой теме.
Ход урока:
1. Актуализация.
1). Вспомним и закрепим понятия, связанные с окружностью и кругом, известные ученикам с 5-ого класса в виде опроса:
а) Что из себя представляет окружность?
Б) С помощью чего можно построить окружность?
В) Что такое круг?
Г) Что такое центр окружности?
Д) Что такое хорда?
Е) что такое радиус?
Ж) Что такое диаметр?
З) Как связаны диаметр и радиус окружности?
И) Что такое дуга окружности?
К) Что такое полуокружность и как ее получить?
Л) Что такое сектор окружности?
Ученики своими словами в свободной форме отвечают на вопросы учителя.
2). Учитель просит учеников с помощью циркуля и линейки начертить в тетради три окружности и самостоятельно отметить элементы окружности, которые только что вспомнили.
2. Лабораторная работа
1) Подготовка.
Ученики раскладывают на парте заранее заготовленный материал и инструменты: 5 предметов цилиндрической формы, нитки, линейка , ножницы.
2) теоретическая часть.
А) Нахождение окружности в цилиндрическом предмете.
Б) длина окружности как периметр круга.
В) Создание проблемной ситуации.
Учитель выслушивает предположения учеников. (Если «опоясать» предмет ниткой, а потом распрямить её и измерить линейкой, то её длина будет приблизительно равна длине окружности) Обозначим её буквой С.
Учитель выслушивает предположения учеников ( На белом листе бумаги обвести круглый предмет, вырезать этот круг и согнуть пополам, измерить линию сгиба линейкой. Эта величина и будет диаметром ). Диаметр обозначим буквой d.
Учитель поясняет, что ответ на этот вопрос может дать анализ результатов лабораторной работы.
Для этого нумеруем предметы и результаты измерений записываем в таблицу. При этом 4-ый столбец оставляем пустым.
Г) Выполнение практической части лабораторной работы. Ученики работают в парах.
Заполнение Таблицы.
Д) Анализ полученных измерений.
Ученики, используя таблицу, пытаются найти ответ на проблемную ситуацию, заданную в лабораторной работе. ( Если никто из учеников не догадался, учитель предлагает вспомнить последние пройденные темы или предлагает напрямую найти отношение длины окружности к её диаметру для каждого измерения)
Е) Вычислительная часть.
В 4-ый столбец считаем и записываем С:d с точностью до десятых.
Ж) Ученики приходят к выводу, что, несмотря на различные цифры во 2-ом и 3-ем столбцах, отношения этих величин приблизительно равны от 3,1 до 3,2.
Записывают вывод: опытным путём было установлено, что так как отношение длины окружности к её диаметру является одним и тем же числом, то длина окружности прямопропорциональна её диаметру. Таким образом связь установлена и проблемная ситуация разрешена.
З) Учитель рассказывает историческую справку о числе 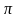 и предлагает ученикам, используя вывод лабораторной работы , вывести формулу длины окружности через её диаметр:
и предлагает ученикам, используя вывод лабораторной работы , вывести формулу длины окружности через её диаметр:
C:d=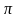
 C=
C=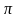 d
d
3. Вспомнив как связаны между собой радиус и диаметр окружности, учитель предлагает ученикам самостоятельно вывести формулу длины окружности через её радиус:
d=2r  C=2
C=2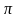 r.
r.
4. Учитель знакомит учеников с формулой площади круга:
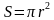
5. Закрепление полученных знаний.
1) Решение задач у доски (решают два ученика) № 851, 855. УМК Н.Я. Виленкин.
Остальные ученики решают самостоятельно , сверяясь с доской.
2). № 854, 856. Решают самостоятельно.
6. Домашнее задание. П.24. №869, 870.
Анализ проведенного урока:
В ходе урока были реализованы все поставленные цели и задачи. В результате практической деятельности у учеников наблюдался повышенный интерес к разрешению проблемной ситуации.
В решении тех задач , где ученики применяли самостоятельно выведенные формулы, наблюдался больший процент успеха, чем в решении тех задач, в которых применялись формулы просто данные учителем







 , самостоятельный вывод формулы длины окружности. Знакомство с формулой площади круга. Применение новых знаний в решении задач.
, самостоятельный вывод формулы длины окружности. Знакомство с формулой площади круга. Применение новых знаний в решении задач.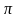 и предлагает ученикам, используя вывод лабораторной работы , вывести формулу длины окружности через её диаметр:
и предлагает ученикам, используя вывод лабораторной работы , вывести формулу длины окружности через её диаметр: C=
C=