``ПРАКТИЧЕСКАЯ РАБОТА №11
«Вычисление производных алгебраических функций»
ЦЕЛЬ РАБОТЫ:
Корректировать знания, умения и навыки в теме: «Вычисление производных алгебраических функций».
Закрепить и систематизировать знания по теме.
Определить уровень усвоения знаний, оценить результат деятельности студента.
ОБОРУДОВАНИЕ: инструкционно-технологические карты, таблица производных элементарных функций; микрокалькуляторы.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ:
Ответить на контрольные вопросы:
а) Сформулируйте определение функции.
б) Сформулируйте правила вычисления производных алгебраических функций.
в) В чем состоит механический смысл производной?
г) Тело движется по прямой согласно закону х(t). Запишите формулы для нахождения скорости и ускорения тела в момент времени t.
По образцу выполнить тренировочные задания.
Изучить условие заданий для практической работы.
Оформить отчет о работе.
УКАЗАНИЯ К ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ
Понятие производной
Если существует конечный пределотношения приращения функции к приращению аргумента при стремлении последнего к 0, то он (предел) называется производной от функции и обозначается одним из следующих символов: 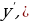
Таким образом: 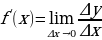
Действие нахождения производной называют дифференцированием.
Правила дифференцирования
1) 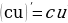 - постоянный множитель можно выносить за знак производной
- постоянный множитель можно выносить за знак производной
2) 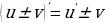 - производная суммы (разности)
- производная суммы (разности)
3) 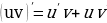 - производная произведения
- производная произведения
4) 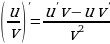 - производная от деления
- производная от деления
Геометрический и физический смысл.
ГЕОМЕТРИЧЕСКИЙ СМЫСЛ
(график касательной к функции 0079)
Дана непрерывная функция y = f(x), x[a; b], дифференцируема в точке x0(a; b)и пусть кривая L – график этой функции. На кривой Lвозьмём произвольную точку М0(x0; y0).
Производная функции f(x) в точке x0 равна угловому коэффициенту касательной, проведённой к графику данной функции в его точке с абсциссой x0.
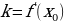
k – этоtg угла наклона касательной с положительным направлением оси Ox.
Уравнение касательной к кривой L в точке (x0; f(x0)) и имеющей угловой коэффициент k = f(x0)
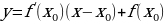
Прямая перпендикулярная к касательной в точке М0 называется нормаль к кривойL в точке М0.
Угловой коэффициент нормали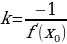
Уравнение нормали к кривойL в точке М0(x0; f(x0))
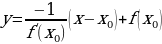
Пример 1. Составить уравнение касательной и нормали к кривой 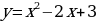 в её точке с абсциссой
в её точке с абсциссой 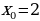
Решение.
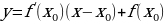 - уравнение касательной
- уравнение касательной
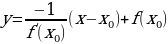 - уравнение нормали
- уравнение нормали
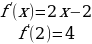
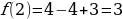
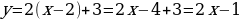 ;
; 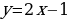 - уравнение касательной
- уравнение касательной
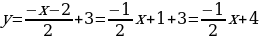 ;
; 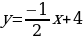 - уравнение нормали
- уравнение нормали
МЕХАНИЧЕСКИЙ СМЫСЛ
Производная 1 – го порядка от пути по времени есть мгновенная скорость.
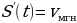
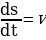
Производная 2 – го порядка от пути по времени есть ускорение.
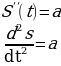
Пример 2. Найти скорость движения точки в момент времени t = 5, если закон движения задан формулой 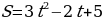
Решение.
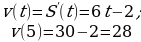
Ответ: 28
ПРИМЕР 1. Решите неравенство: 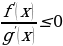 , если
, если 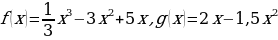 .
.
РЕШЕНИЕ. Пользуясь правилами дифференцирования алгебраических функций и формулами дифференцирования элементарных функций, вычислим производные:
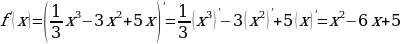 ;
;
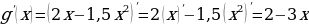 .
.
Таким образом, нужно решить неравенство:
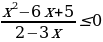 .
.
Разложим числитель дроби на множители:
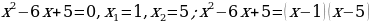 .
.
Неравенство 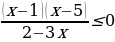 методом интервалов.
методом интервалов.

Нули числителя: х = 1, х = 5. Нуль знаменателя: 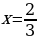 .
.
О т в е т: 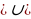 .
.
ПРИМЕР 2. Тело движется по прямой согласно закону 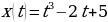 . Найдите скорость и ускорение точки в момент времени
. Найдите скорость и ускорение точки в момент времени 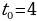 .
.
РЕШЕНИЕ. Скорость движения – это производная от пути по времени, следовательно,
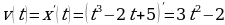 .
.
Значит, в момент времени 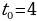 скорость данного движения такова:
скорость данного движения такова: 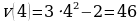 .
.
Так как нам известна скорость движения как функция времени, мы можем найти ускорение этого движения: 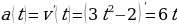 .
.
Значит, в момент времени 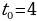 ускорение данного движения равно:
ускорение данного движения равно: 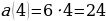 .
.
О т в е т: 46; 24.
ЗАДАНИЯ ДЛЯ САМОКОНТРОЛЯ.
Решите неравенство 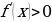 , если
, если 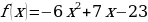 .
.
Тело движется по прямой согласно закону 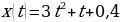 . Найдите скорость и ускорение точки в момент времени
. Найдите скорость и ускорение точки в момент времени 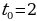 .
.
ВАРИАНТЫ ПРАКТИЧЕСКОЙ РАБОТЫ
Вариант 1.
Пользуясь формулами и правилами дифференцирования, найдите производные 1 и 2 порядка функций:
а) f(x)=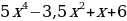 ; б) f(x)=
; б) f(x)=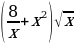 ; в) f(x)=
; в) f(x)=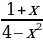 .
.
г)f(x)=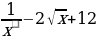 ; д)f (x)=
; д)f (x)=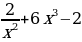 ; е) f(x)=
; е) f(x)=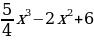 ж)
ж) 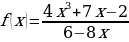
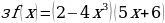 и)
и)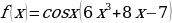 к)
к) 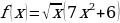
л) 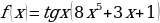 м)
м) 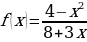 н)
н) 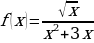 о)
о) 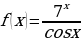
Решите уравнение 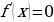 , если
, если 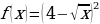 .
.
Вариант 2.
Пользуясь формулами и правилами дифференцирования, найдите производные функций:
а) 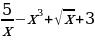 ; б)
; б) 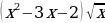 ; в)
; в) 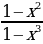 .
.
г)f(x)=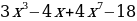 ; д) f (x)=
; д) f (x)=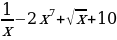 ; е) f(x)=
; е) f(x)=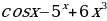
ж) 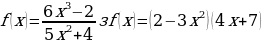 и)
и)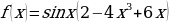
к) 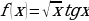 л)
л) 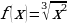 +6x-7 м)
+6x-7 м) 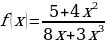 о)
о) 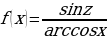
Решите неравенство 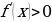 , если
, если 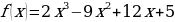 .
.
Вариант 3.
Пользуясь формулами и правилами дифференцирования, найдите производные функций:
а) f(x)=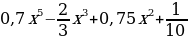 ; б) f(x)=
; б) f(x)=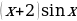 ; в) f(x)=
; в) f(x)=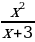 .
.
г)f(x)=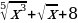 ; д)f (x)=
; д)f (x)=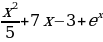 ; е) f(x)=
; е) f(x)=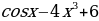 x+
x+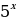
ж) 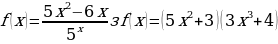 и)
и)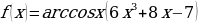
к) 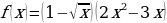 л)
л) 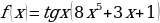 м)
м) 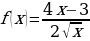
н) 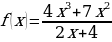 о)
о) 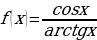
Решите уравнение 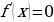 , если
, если 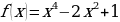 .
.
Вариант 4.
Пользуясь формулами и правилами дифференцирования, найдите производные функций:
а) f(x)=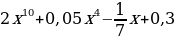 ; б)f(x)=
; б)f(x)= 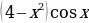 ; в) f(x)=
; в) f(x)=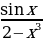
г)f(x)=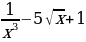 ; д)f (x)=
; д)f (x)=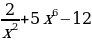 ; е) f(x)=
; е) f(x)=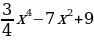
ж) 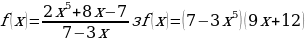 и)
и)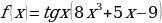
к) 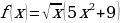 л)
л) 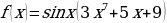
м) 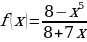 н)
н) 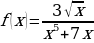 о)
о) 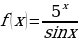
Решите уравнение 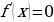 , если
, если 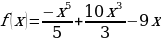 .
.
Вариант 5.
Пользуясь формулами и правилами дифференцирования, найдите производные функций:
а) 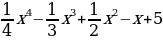 ; б)y=
; б)y=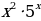 ; в) y=
; в) y=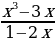 .
.
г)f(x)=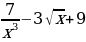 ; д)f (x)=
; д)f (x)=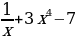 ; е) f(x)=
; е) f(x)=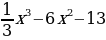 ж)
ж) 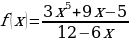
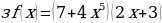 и)
и)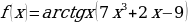 к)
к) 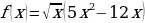
л) 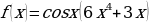 м)
м) 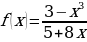 н)
н) 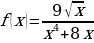 о)
о) 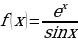
Решите уравнение 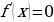 , если
, если 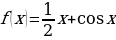 .
.
Вариант 6.
Пользуясь формулами и правилами дифференцирования, найдите производные функций:
а)y=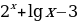 ; б) y=
; б) y=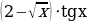 ; в) y=
; в) y=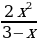
г)f(x)=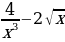 ; д)f (x)=
; д)f (x)=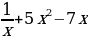 ; е) f(x)=
; е) f(x)=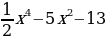 ж)
ж) 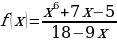
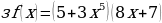 и)
и)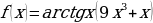 к)
к) 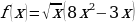
л) 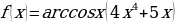 м)
м) 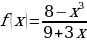 н)
н) 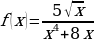 о)
о) 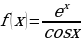
Материальная точка движется прямолинейно по закону 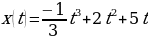 . Через сколько секунд после начала движения точка остановится?
. Через сколько секунд после начала движения точка остановится?
Вариант 7.
Пользуясь формулами и правилами дифференцирования, найдите производные функций:
а)y=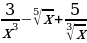 ; б) y=
; б) y=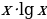 ; в)y=
; в)y=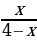 .
.
г)f(x)=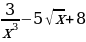 ; д)f (x)=
; д)f (x)=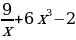 ; е) f(x)=
; е) f(x)=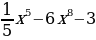 ж)
ж) 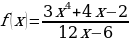
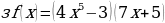 и)
и)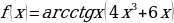 к)
к) 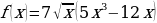
л) 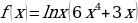 м)
м) 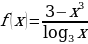 н)
н) 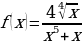 о)
о) 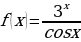
Найдите х, при котором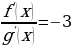 , если
, если 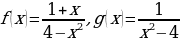 .
.
Вариант 8.
Пользуясь формулами и правилами дифференцирования, найдите производные функций:
а) y=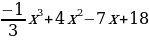 ; б) y=
; б) y=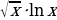 ; в) y=
; в) y=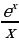 .
.
г)f(x)=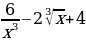 ; д)f (x)=
; д)f (x)=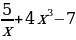 ; е) f(x)=
; е) f(x)=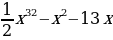 ж)
ж) 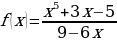
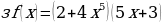 и)
и)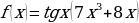 к)
к) 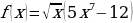
л) 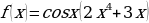 м)
м) 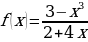 н)
н) 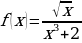 о)
о) 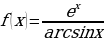
По прямой движутся две материальные точки по законам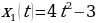 и
и 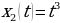 . В каком промежутке времени скорость первой точки больше скорости второй?
. В каком промежутке времени скорость первой точки больше скорости второй?





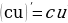 - постоянный множитель можно выносить за знак производной
- постоянный множитель можно выносить за знак производной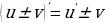 - производная суммы (разности)
- производная суммы (разности)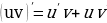 - производная произведения
- производная произведения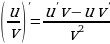 - производная от деления
- производная от деления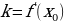
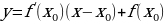
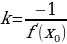
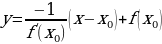
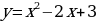 в её точке с абсциссой
в её точке с абсциссой 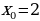
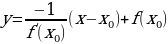 - уравнение нормали
- уравнение нормали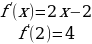
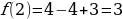
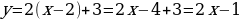 ;
; 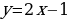 - уравнение касательной
- уравнение касательной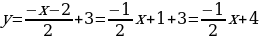 ;
; 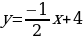 - уравнение нормали
- уравнение нормали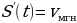
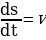
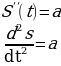
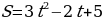
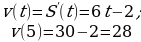
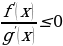 , если
, если 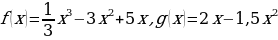 .
.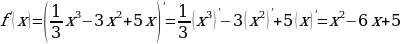 ;
;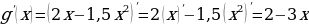 .
.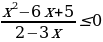 .
.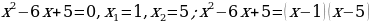 .
.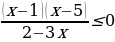 методом интервалов.
методом интервалов. 
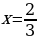 .
.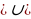 .
.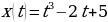 . Найдите скорость и ускорение точки в момент времени
. Найдите скорость и ускорение точки в момент времени 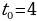 .
.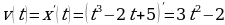 .
.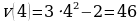 .
.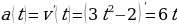 .
.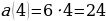 .
.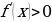 , если
, если 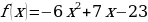 .
.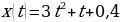 . Найдите скорость и ускорение точки в момент времени
. Найдите скорость и ускорение точки в момент времени 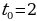 .
.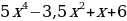 ; б) f(x)=
; б) f(x)=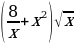 ; в) f(x)=
; в) f(x)=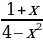 .
. 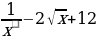 ; д)f (x)=
; д)f (x)=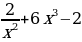 ; е) f(x)=
; е) f(x)=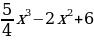 ж)
ж) 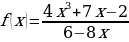
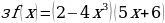 и)
и)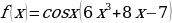 к)
к) 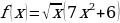
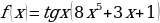 м)
м) 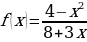 н)
н) 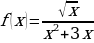 о)
о) 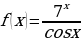
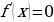 , если
, если 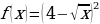 .
.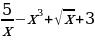 ; б)
; б) 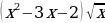 ; в)
; в) 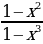 .
.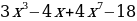 ; д) f (x)=
; д) f (x)=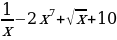 ; е) f(x)=
; е) f(x)=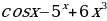
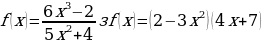 и)
и)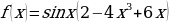
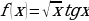 л)
л) 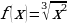 +6x-7 м)
+6x-7 м) 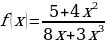 о)
о) 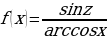
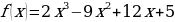 .
.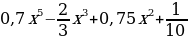 ; б) f(x)=
; б) f(x)=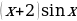 ; в) f(x)=
; в) f(x)=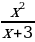 .
.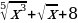 ; д)f (x)=
; д)f (x)=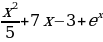 ; е) f(x)=
; е) f(x)=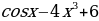 x+
x+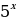
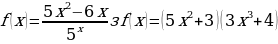 и)
и)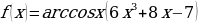
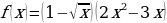 л)
л) 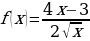
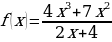 о)
о) 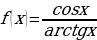
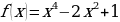 .
.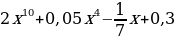 ; б)f(x)=
; б)f(x)= 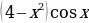 ; в) f(x)=
; в) f(x)=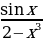
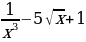 ; д)f (x)=
; д)f (x)=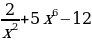 ; е) f(x)=
; е) f(x)=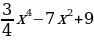
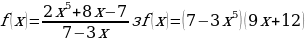 и)
и)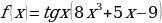
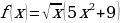 л)
л) 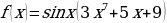
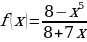 н)
н) 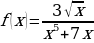 о)
о) 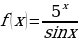
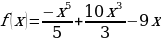 .
.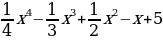 ; б)y=
; б)y=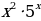 ; в) y=
; в) y=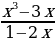 .
.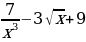 ; д)f (x)=
; д)f (x)=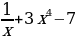 ; е) f(x)=
; е) f(x)=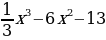 ж)
ж) 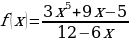
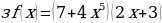 и)
и)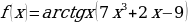 к)
к) 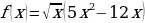
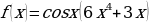 м)
м) 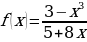 н)
н) 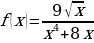 о)
о) 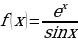
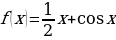 .
.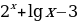 ; б) y=
; б) y=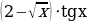 ; в) y=
; в) y=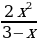
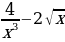 ; д)f (x)=
; д)f (x)=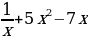 ; е) f(x)=
; е) f(x)=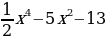 ж)
ж) 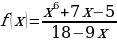
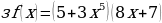 и)
и)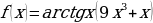 к)
к) 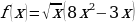
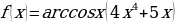 м)
м) 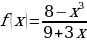 н)
н) 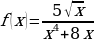 о)
о) 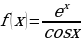
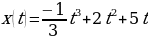 . Через сколько секунд после начала движения точка остановится?
. Через сколько секунд после начала движения точка остановится?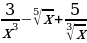 ; б) y=
; б) y=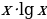 ; в)y=
; в)y=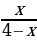 .
.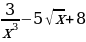 ; д)f (x)=
; д)f (x)=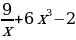 ; е) f(x)=
; е) f(x)=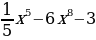 ж)
ж) 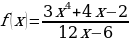
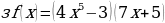 и)
и)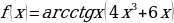 к)
к) 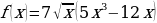
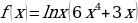 м)
м) 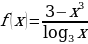 н)
н) 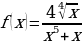 о)
о) 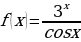
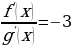 , если
, если 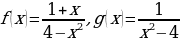 .
.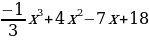 ; б) y=
; б) y=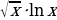 ; в) y=
; в) y=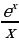 .
.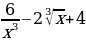 ; д)f (x)=
; д)f (x)=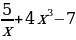 ; е) f(x)=
; е) f(x)=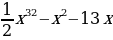 ж)
ж) 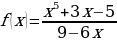
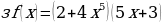 и)
и)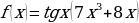 к)
к) 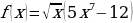
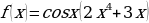 м)
м) 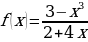 н)
н) 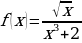 о)
о) 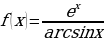
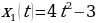 и
и 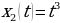 . В каком промежутке времени скорость первой точки больше скорости второй?
. В каком промежутке времени скорость первой точки больше скорости второй?









